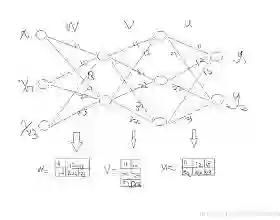
Feedback-rich neural architectures can regenerate earlier representations and inject temporal context, making them a natural setting for strictly local synaptic plasticity. We ask whether a minimal, backpropagation-free feedback--Hebbian system can already express interpretable continual-learning--relevant behaviors under controlled training schedules. We introduce a compact prediction--reconstruction architecture with two feedforward layers for supervised association learning and two dedicated feedback layers trained to reconstruct earlier activity and re-inject it as additive temporal context. All synapses are updated by a unified local rule combining centered Hebbian covariance, Oja-style stabilization, and a local supervised drive where targets are available, requiring no weight transport or global error backpropagation. On a small two-pair association task, we characterize learning through layer-wise activity snapshots, connectivity trajectories (row/column means of learned weights), and a normalized retention index across phases. Under sequential A->B training, forward output connectivity exhibits a long-term depression (LTD)-like suppression of the earlier association while feedback connectivity preserves an A-related trace during acquisition of B. Under deterministic interleaving A,B,A,B,..., both associations are concurrently maintained rather than sequentially suppressed. Architectural controls and rule-term ablations isolate the role of dedicated feedback in regeneration and co-maintenance, and the role of the local supervised term in output selectivity and unlearning. Together, the results show that a compact feedback pathway trained with local plasticity can support regeneration and continual-learning--relevant dynamics in a minimal, mechanistically transparent setting.

翻译：反馈丰富的神经架构能够再生早期表征并注入时间上下文，使其成为严格局部突触可塑性的天然场景。我们探究一个最小化的、无反向传播的反馈-赫布系统是否能在受控训练计划下已能表达可解释的持续学习相关行为。我们提出一种紧凑的预测-重构架构，包含两个用于监督关联学习的前馈层和两个专用反馈层，后者被训练用于重构早期活动并将其作为加性时间上下文重新注入。所有突触均通过统一的局部规则更新，该规则结合了中心化赫布协方差、Oja式稳定化以及目标可用时的局部监督驱动，无需权重传递或全局误差反向传播。在一个小型双关联任务中，我们通过逐层活动快照、连接轨迹（学习权重的行/列均值）以及跨阶段的归一化保持指数来表征学习过程。在顺序A->B训练下，前向输出连接表现出对早期关联的长时程抑制样抑制，而反馈连接在B的获取期间保留了与A相关的痕迹。在确定性交错训练A,B,A,B,...下，两个关联被同时维持而非顺序抑制。架构控制和规则项消融实验分离了专用反馈在再生与协同维持中的作用，以及局部监督项在输出选择性和遗忘中的作用。综合结果表明，通过局部可塑性训练的紧凑反馈通路能够在最小化、机制透明的场景中支持再生和持续学习相关的动力学。