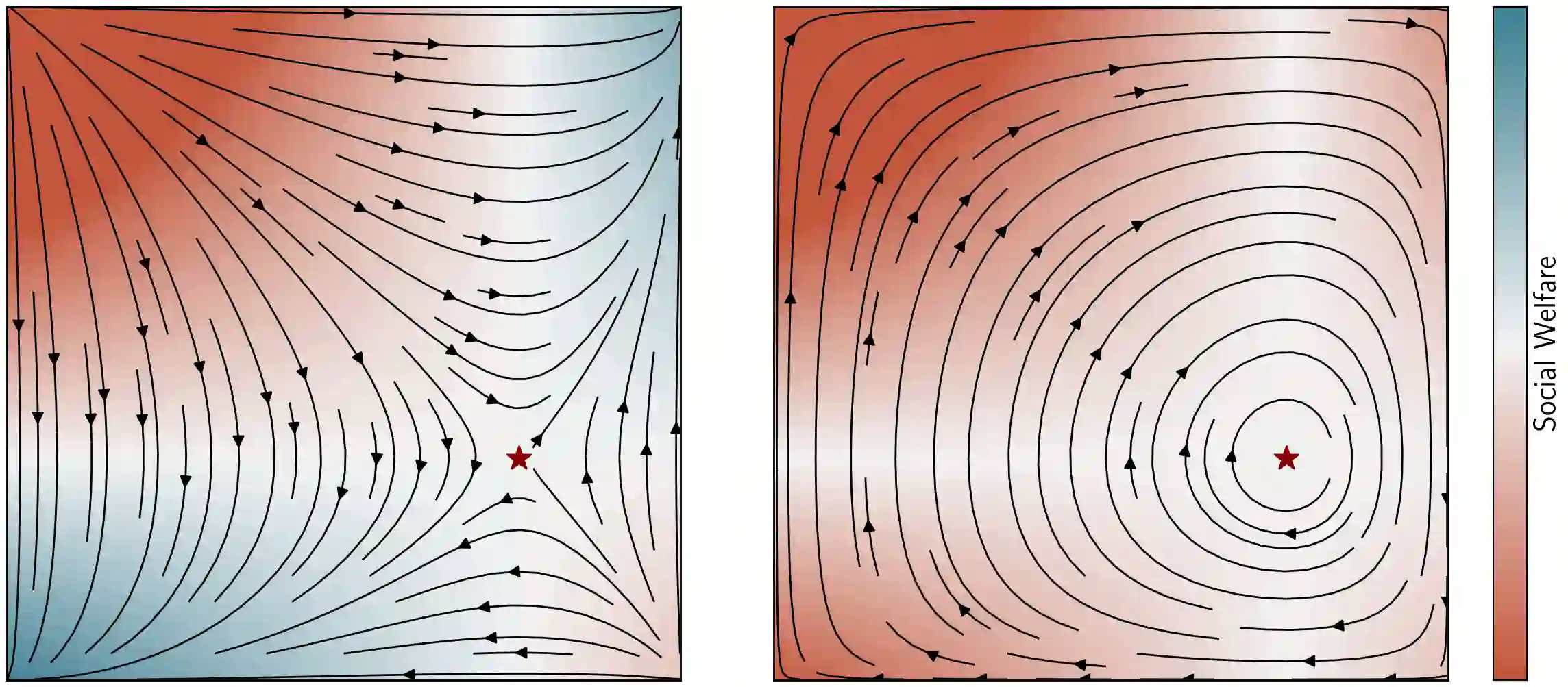
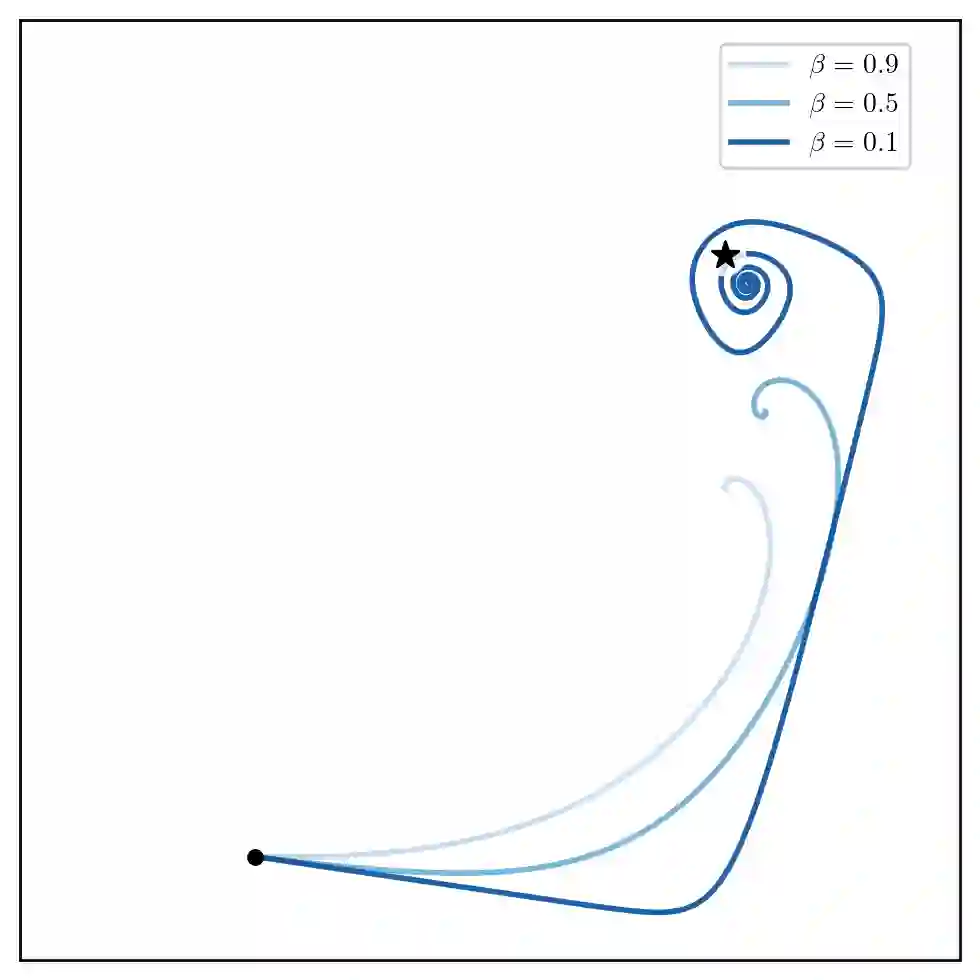
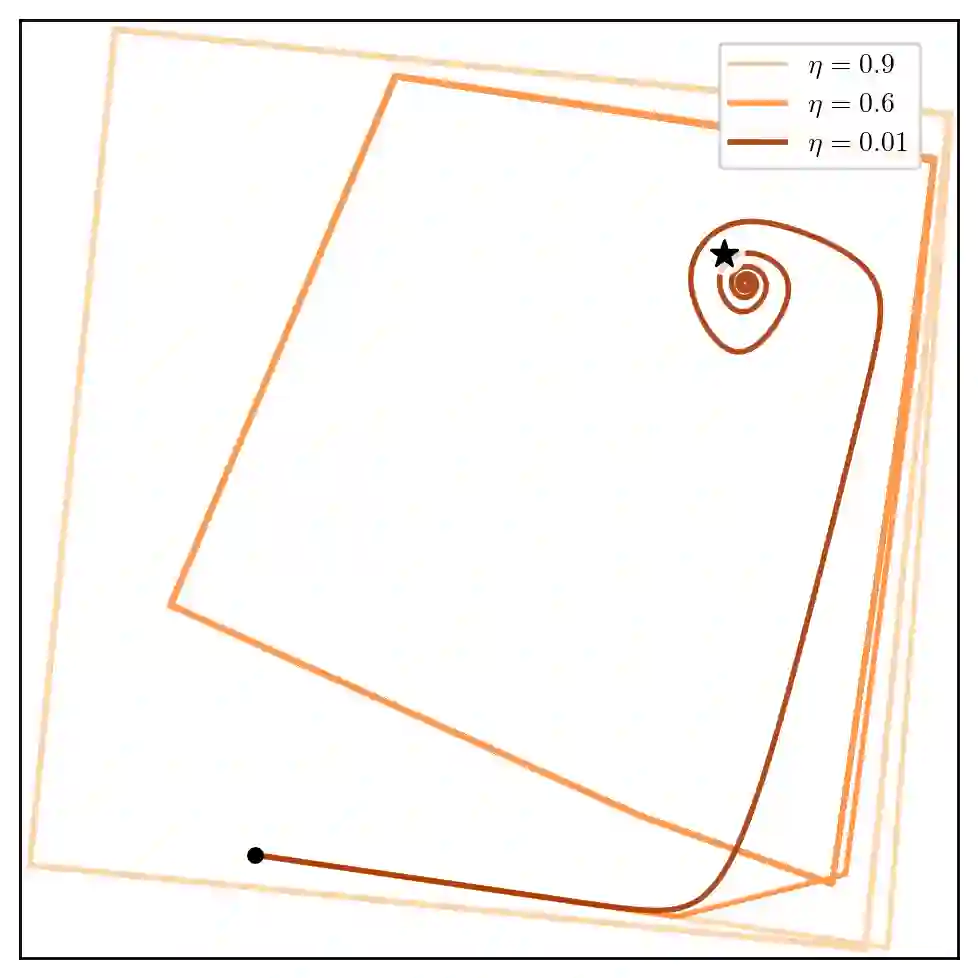
We extend the study of learning in games to dynamics that exhibit non-asymptotic stability. We do so through the notion of uniform stability, which is concerned with equilibria of individually utility-seeking dynamics. Perhaps surprisingly, it turns out to be closely connected to economic properties of collective rationality. Under mild non-degeneracy conditions and up to strategic equivalence, if a mixed equilibrium is not uniformly stable, then it is not weakly Pareto optimal: there is a way for all players to improve by jointly deviating from the equilibrium. On the other hand, if it is locally uniformly stable, then the equilibrium must be weakly Pareto optimal. Moreover, we show that uniform stability determines the last-iterate convergence behavior for the family of incremental smoothed best-response dynamics, used to model individual and corporate behaviors in the markets. Unlike dynamics around strict equilibria, which can stabilize to socially-inefficient solutions, individually utility-seeking behaviors near mixed Nash equilibria lead to collective rationality.

翻译：我们将博弈学习的研究扩展到展现非渐近稳定性的动态过程。通过均匀稳定性的概念实现这一扩展，该概念关注个体效用寻求动态的均衡状态。或许令人惊讶的是，这一概念与集体理性的经济特性存在紧密联系。在温和的非退化条件下且直至策略等价性，若混合均衡不具备均匀稳定性，则其必然不是弱帕累托最优：存在所有参与者通过联合偏离均衡而实现共同改进的途径。反之，若该均衡具有局部均匀稳定性，则其必定满足弱帕累托最优性。此外，我们证明均匀稳定性决定了增量平滑最优响应动态族（用于模拟市场中个体与企业行为）的末次迭代收敛特性。与严格均衡周围的动态（可能稳定于社会低效解）不同，混合纳什均衡附近的个体效用寻求行为将导向集体理性。