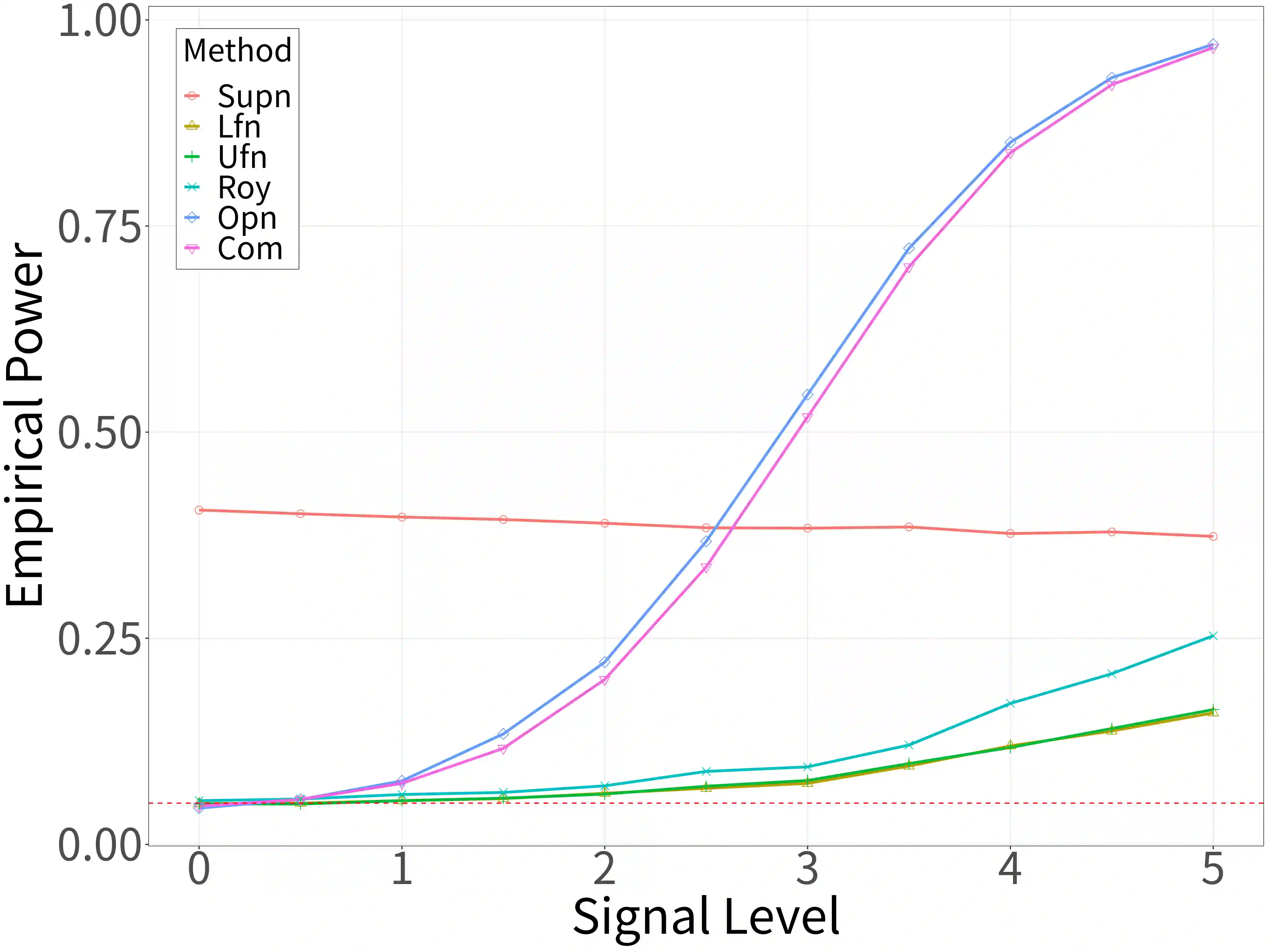
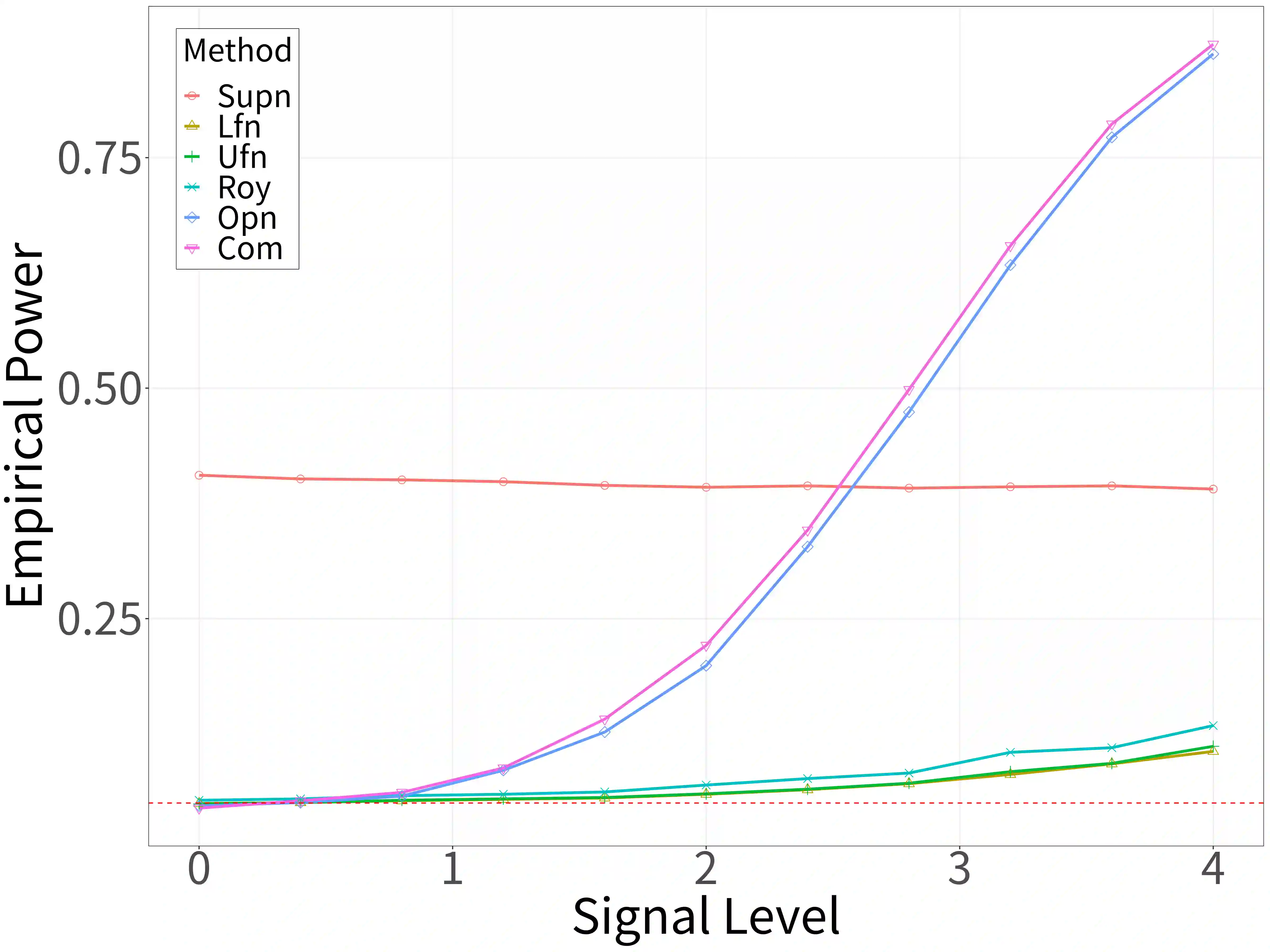
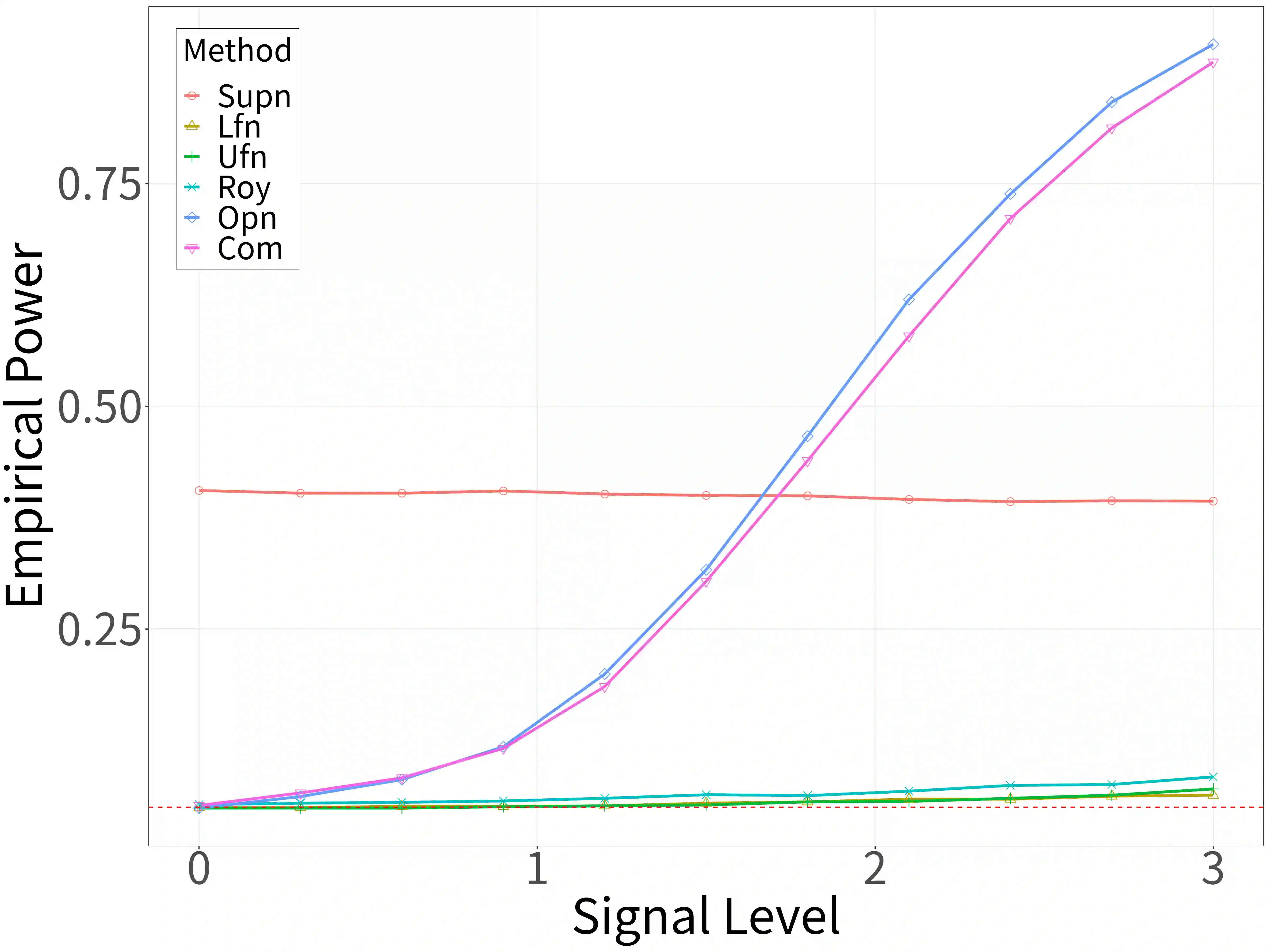
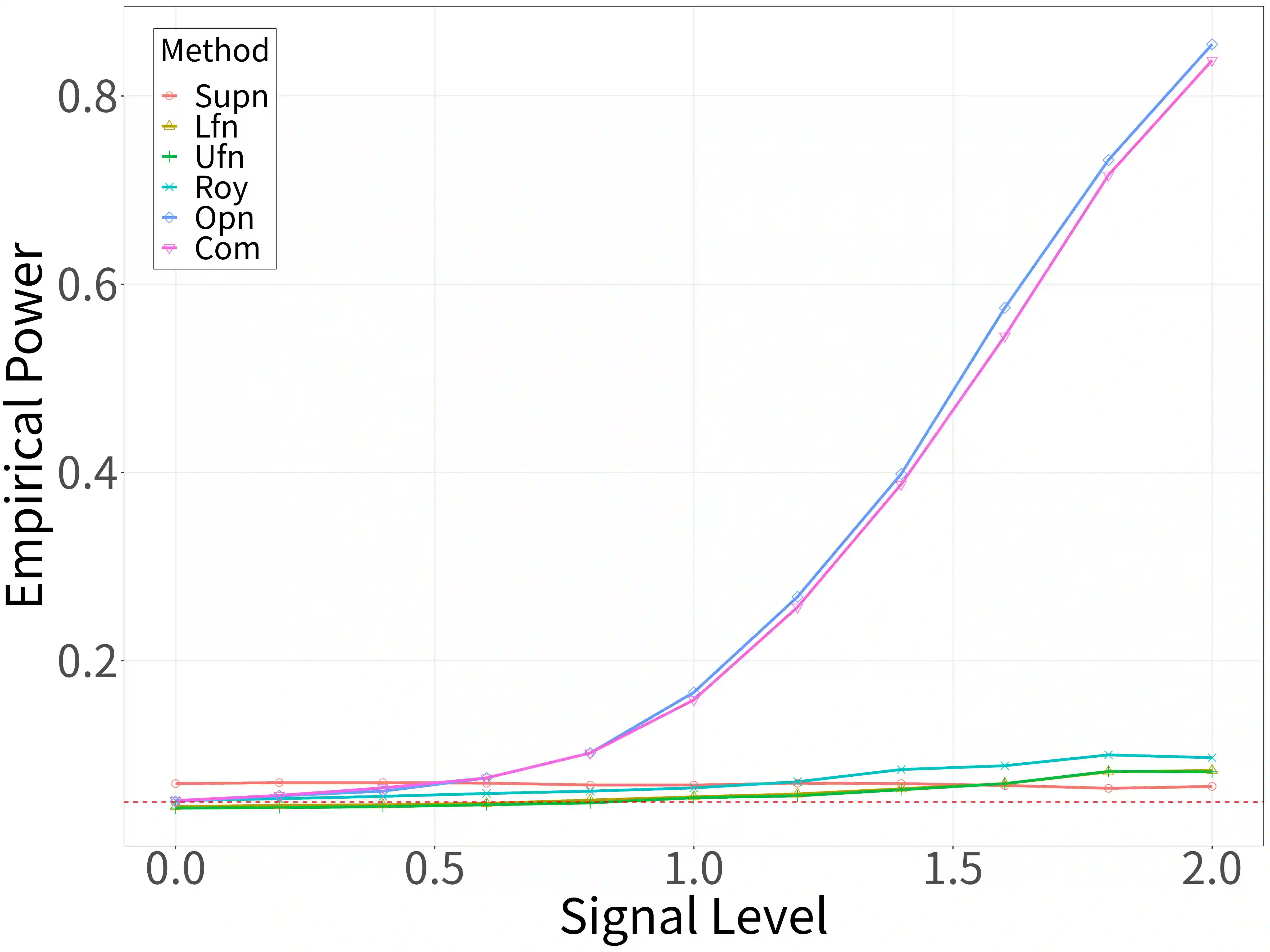
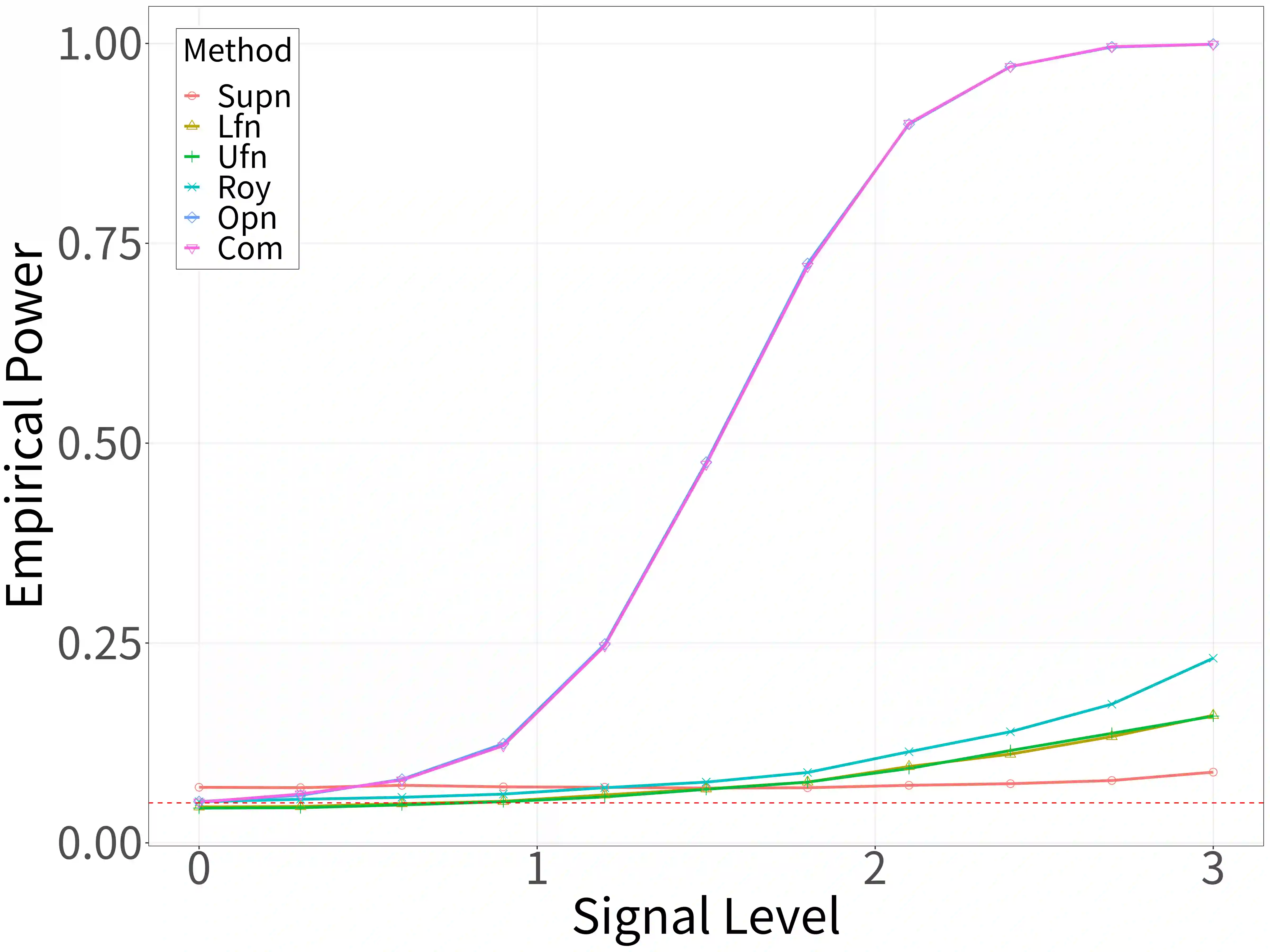
Spectral analysis plays a crucial role in high-dimensional statistics, where determining the asymptotic distribution of various spectral statistics remains a challenging task. Due to the difficulties of deriving the analytic form, recent advances have explored data-driven bootstrap methods for this purpose. However, widely used Gaussian approximation-based bootstrap methods, such as the empirical bootstrap and multiplier bootstrap, have been shown to be inconsistent in approximating the distributions of spectral statistics in high-dimensional settings. To address this issue, we propose a universal bootstrap procedure based on the concept of universality from random matrix theory. Our method consistently approximates a broad class of spectral statistics across both high- and ultra-high-dimensional regimes, accommodating scenarios where the dimension-to-sample-size ratio $p/n$ converges to a nonzero constant or diverges to infinity without requiring structural assumptions on the population covariance matrix, such as eigenvalue decay or low effective rank. We showcase this universal bootstrap method for high-dimensional covariance inference. Extensive simulations and a real-world data study support our findings, highlighting the favorable finite sample performance of the proposed universal bootstrap procedure.

翻译：谱分析在高维统计中扮演着关键角色，其中确定各类谱统计量的渐近分布仍是一项具有挑战性的任务。由于推导解析形式的困难，近期研究探索了基于数据驱动的自助法来解决此问题。然而，广泛使用的基于高斯近似的自助法（如经验自助法和乘数自助法）已被证明在高维设定下近似谱统计量分布时存在不一致性。为解决这一问题，我们基于随机矩阵理论中的普适性概念，提出了一种普适性自助法流程。该方法能一致地近似涵盖高维与超高维体系下的一类广泛谱统计量，适应维度-样本量比$p/n$收敛于非零常数或发散至无穷的情形，且无需对总体协方差矩阵施加结构假设（如特征值衰减或低有效秩）。我们展示了这一普适性自助法在高维协方差推断中的应用。大量模拟实验与一项真实世界数据研究验证了我们的结论，突显了所提出的普适性自助法在有限样本下的优异性能。