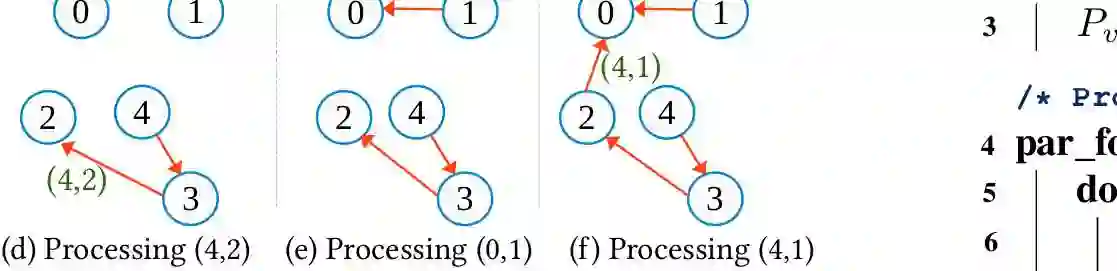
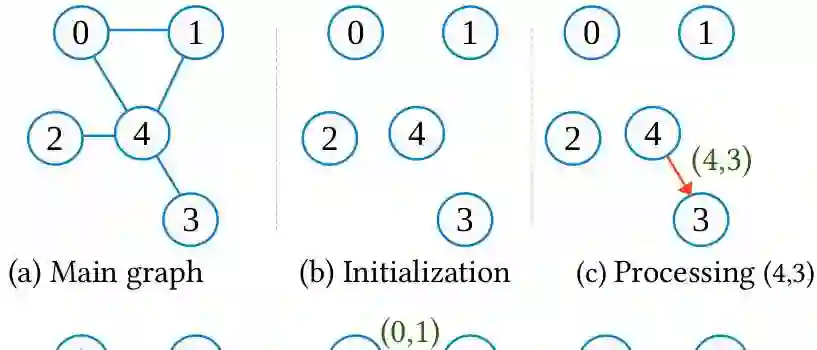
Connected Components (CC) is a core graph problem with numerous applications. This paper investigates accelerating distributed CC by optimizing memory and network bandwidth utilization. We present two novel distributed CC algorithms, SiskinCC and RobinCC, which are built upon the Jayanti-Tarjan disjoint set union algorithm. To optimize memory utilization, SiskinCC and RobinCC are designed to facilitate efficient access to a shared array for all cores running in a machine. This allows execution of faster algorithms with larger memory bounds. SiskinCC leverages the continuous inter-machine communication during the computation phase to reduce the final communication overhead and RobinCC leverages the structural properties of real-world graphs to optimize network bandwidth utilization. Our evaluation against a distributed state-of-the-art CC algorithm, using real-world and synthetic graphs with up to 500 billion edges and 11.7 billion vertices, and on up to 2048 CPU cores, demonstrates that SiskinCC and RobinCC achieve geometric mean speedups of 29.1 and 16.8 times.

翻译：连通分量（CC）是图论中的核心问题，具有广泛的应用。本文通过优化内存与网络带宽利用率来加速分布式连通分量计算。我们提出了两种新颖的分布式连通分量算法——SiskinCC与RobinCC，其构建于Jayanti-Tarjan并查集算法基础之上。为优化内存利用率，SiskinCC与RobinCC被设计为支持单机内所有核心高效访问共享数组，从而能够在更大内存边界下执行更快速的算法。SiskinCC利用计算阶段持续的机器间通信来降低最终通信开销，而RobinCC则利用现实世界图的结构特性来优化网络带宽利用率。我们在包含高达5000亿条边和117亿个顶点的真实世界图与合成图上，使用最多2048个CPU核心，与当前最先进的分布式连通分量算法进行对比评估。实验结果表明，SiskinCC与RobinCC分别实现了29.1倍与16.8倍的几何平均加速比。