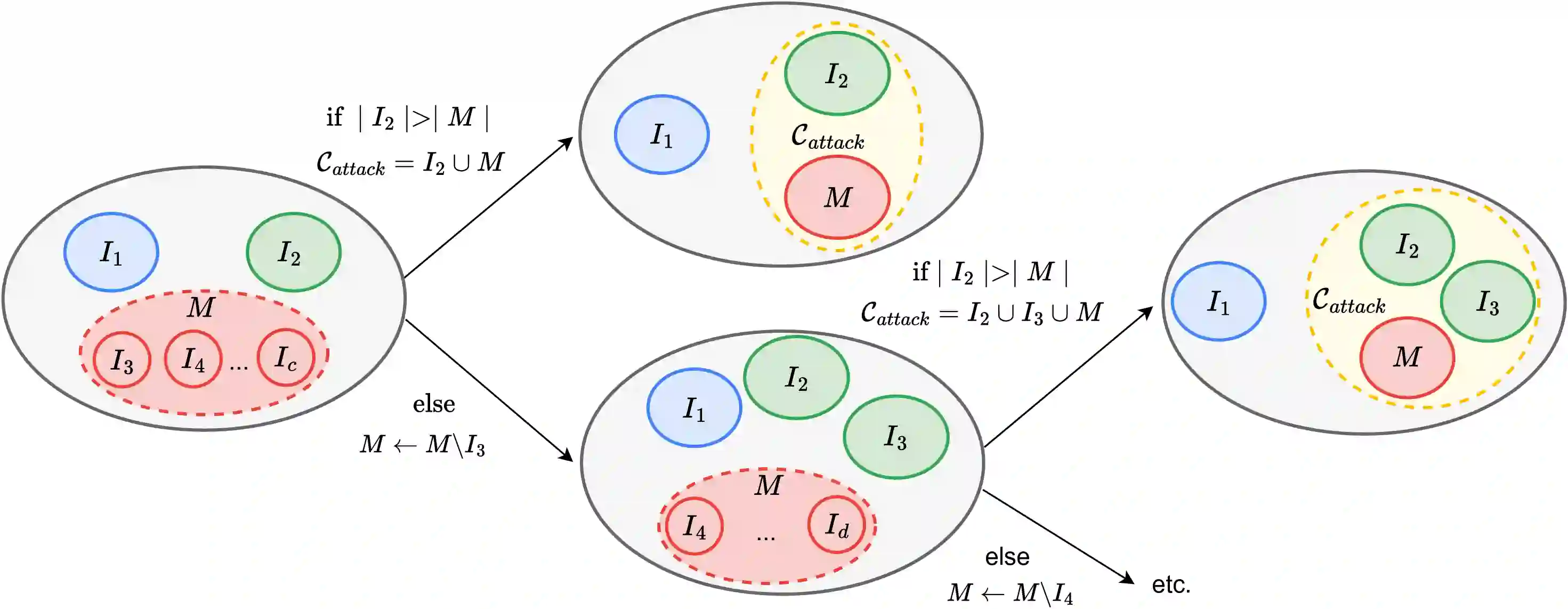
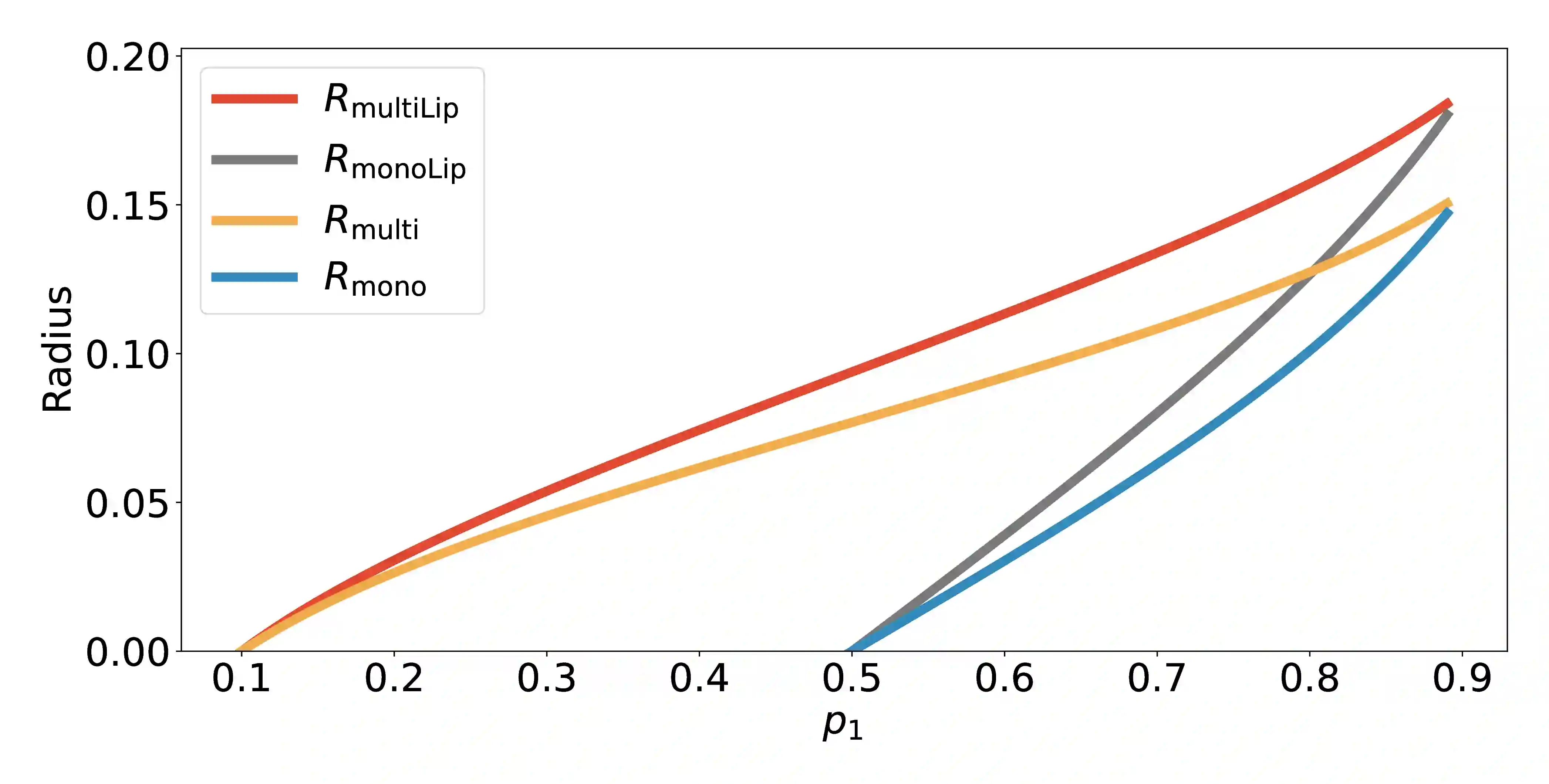
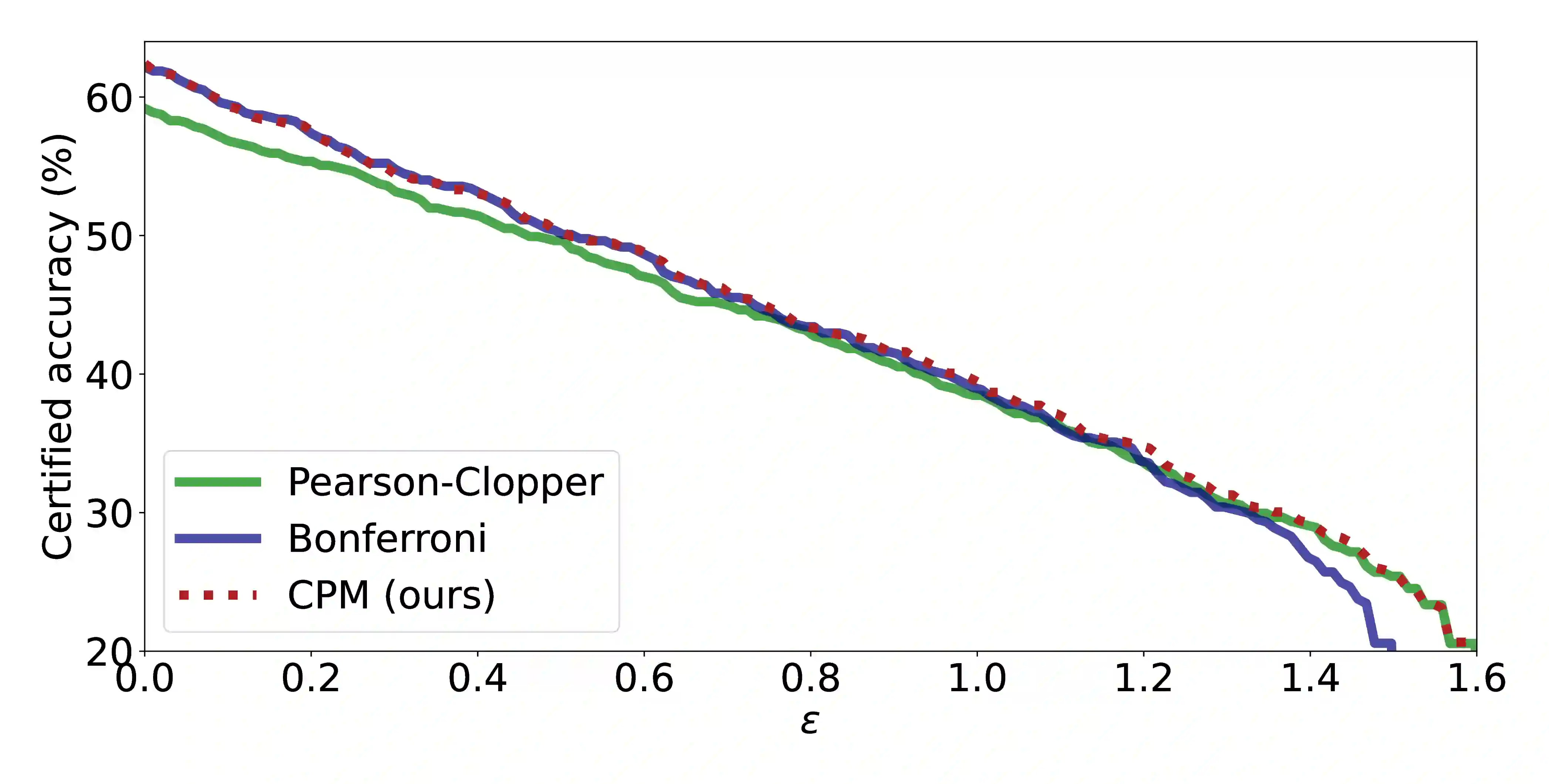
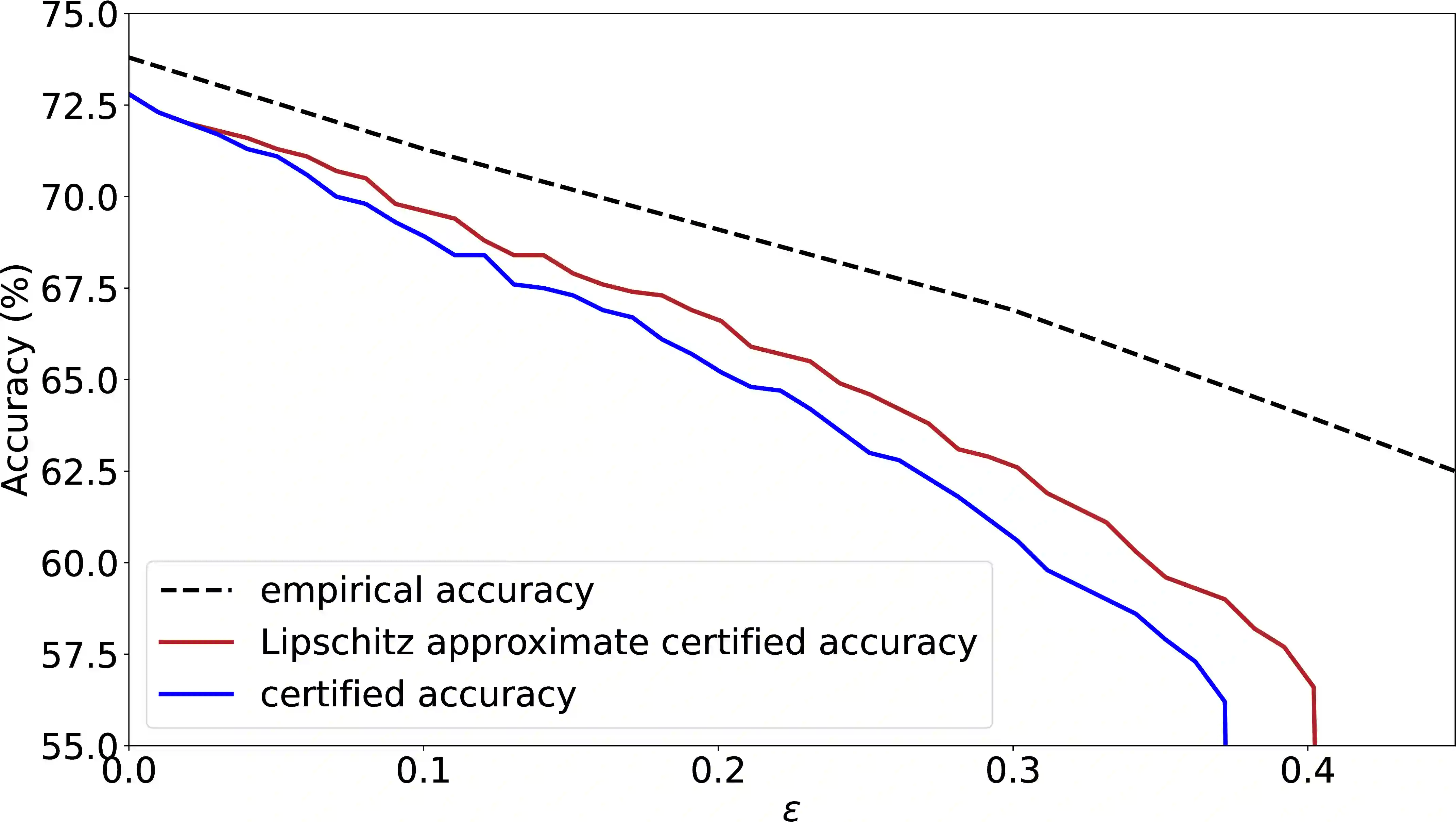
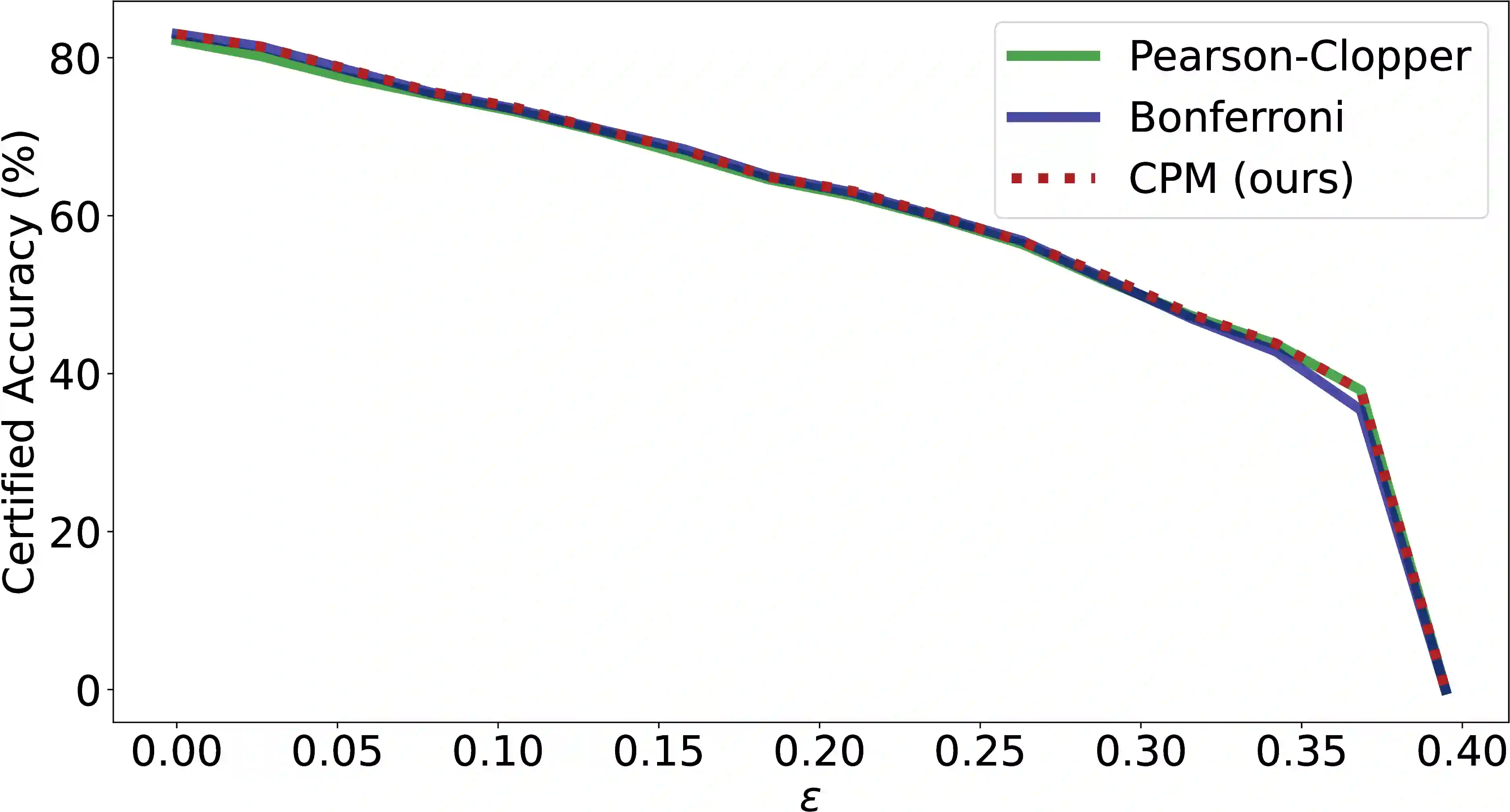
Randomized smoothing has become a leading approach for certifying adversarial robustness in machine learning models. However, a persistent gap remains between theoretical certified robustness and empirical robustness accuracy. This paper introduces a new framework that bridges this gap by leveraging Lipschitz continuity for certification and proposing a novel, less conservative method for computing confidence intervals in randomized smoothing. Our approach tightens the bounds of certified robustness, offering a more accurate reflection of model robustness in practice. Through rigorous experimentation we show that our method improves the robust accuracy, compressing the gap between empirical findings and previous theoretical results. We argue that investigating local Lipschitz constants and designing ad-hoc confidence intervals can further enhance the performance of randomized smoothing. These results pave the way for a deeper understanding of the relationship between Lipschitz continuity and certified robustness.

翻译：随机平滑已成为验证机器学习模型对抗鲁棒性的主流方法。然而，理论认证鲁棒性与实证鲁棒性精度之间始终存在差距。本文提出一种新框架，通过利用Lipschitz连续性进行认证，并提出一种新颖且更少保守的随机平滑置信区间计算方法，从而弥合这一鸿沟。我们的方法收紧了认证鲁棒性的边界，更准确地反映了模型在实际中的鲁棒性。通过严格的实验验证，我们证明该方法提升了鲁棒精度，缩小了实证结果与先前理论结论之间的差距。我们认为，研究局部Lipschitz常数并设计针对性置信区间可进一步提升随机平滑的性能。这些结果为深入理解Lipschitz连续性与认证鲁棒性之间的关系奠定了基础。