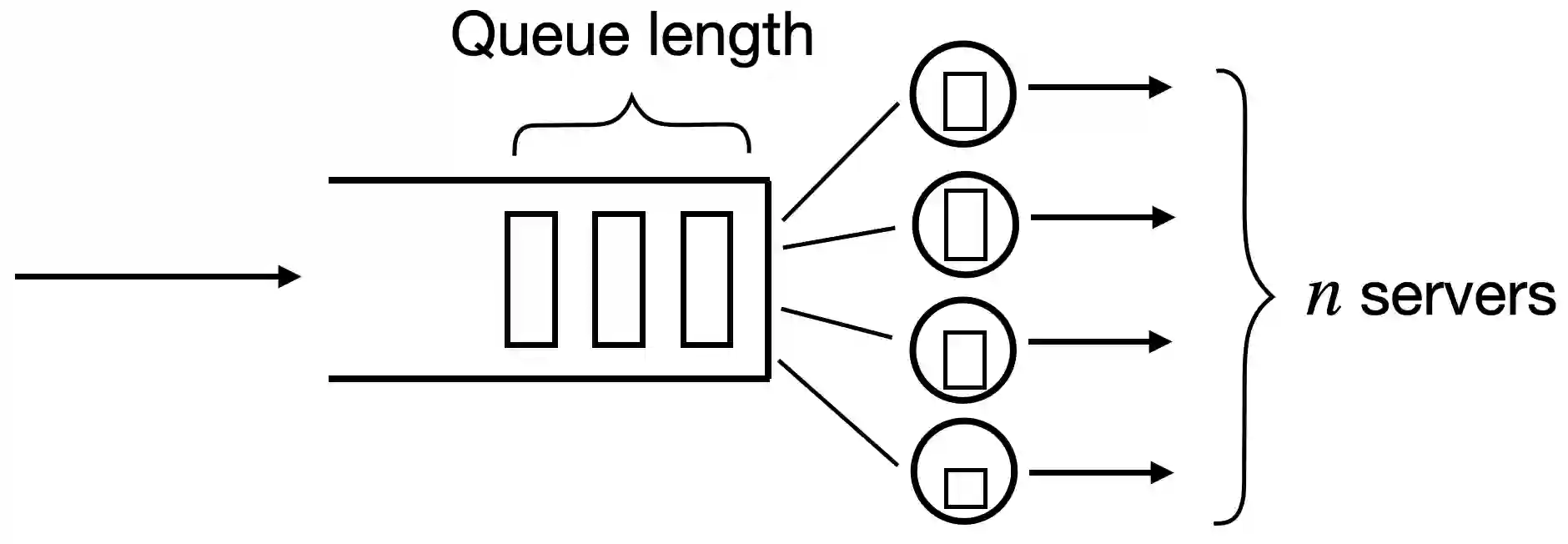
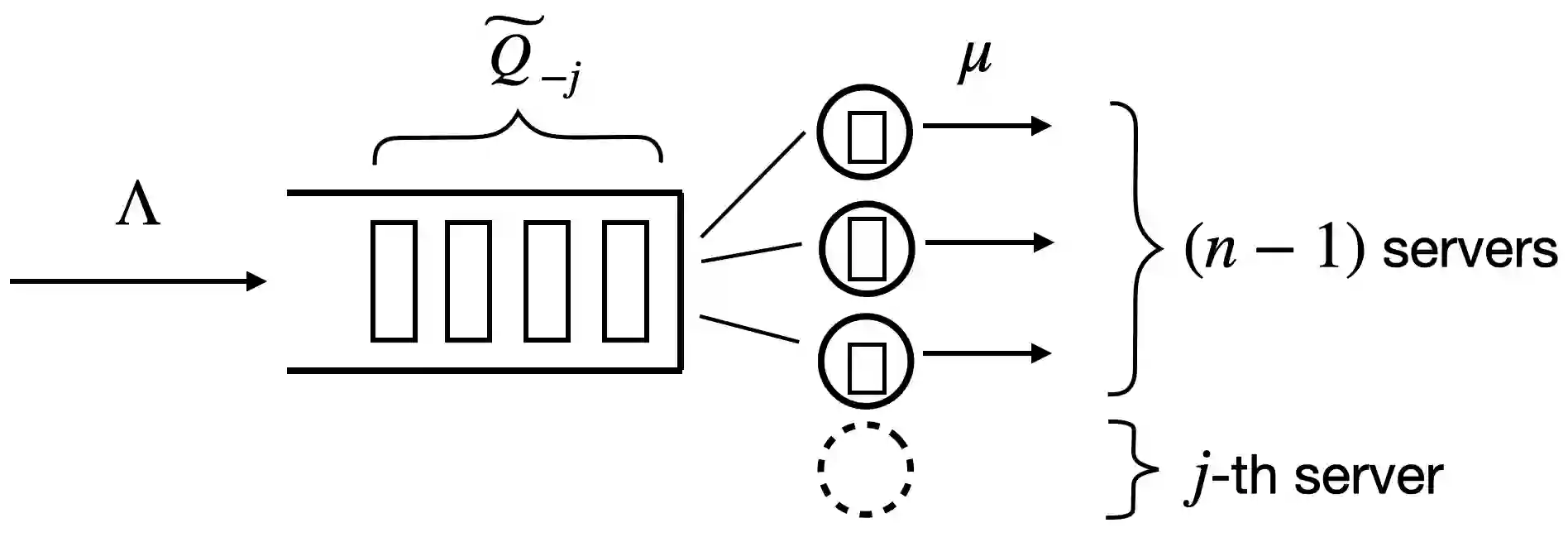
Bounding the queue length in a multiserver queue is a central challenge in queueing theory. Even for the classic $GI/GI/n$ queue with homogeneous servers, it is highly non-trivial to derive a simple and accurate bound for the steady-state queue length that holds across all scaling regimes. A recent breakthrough by Li and Goldberg (2025) establishes bounds that scale as $1/(1-\rho)$ for any load $\rho < 1$ and number of servers $n$, which is the correct scaling in many well-known scaling regimes, including classic heavy-traffic, Halfin-Whitt and Nondegenerate-Slowdown. However, their bounds entail large constant factors and a highly intricate proof, suggesting room for further improvement. In this paper, we present a new $1/(1-\rho)$-scaling bound for the $GI/GI/n$ queue. Our bound, while restricted to the light-tailed case and the first moment of the queue length, has a more interpretable and often tighter leading constant. Our proof is relatively simple, utilizing a modified $GI/GI/n$ queue, the stationarity of a quadratic test function, and a novel leave-one-out coupling technique. Finally, we also extend our method to $GI/GI/n$ queues with fully heterogeneous service-time distributions.

翻译：在多服务器队列中界定队列长度是排队论的核心难题。即便对于具有同质服务器的经典$GI/GI/n$队列，要推导出一个在所有尺度机制下均成立、简单且准确的稳态队列长度界也极具挑战性。Li与Goldberg（2025）近期取得突破性进展，建立了对于任意负载$\rho < 1$及任意服务器数量$n$均按$1/(1-\rho)$尺度变化的界，该尺度在包括经典重负载、Halfin-Whitt机制与非退化减速机制在内的多种著名尺度机制中均被证明是准确的。然而，他们的界包含较大的常数因子，且证明过程极为复杂，表明仍有进一步改进的空间。本文针对$GI/GI/n$队列提出了一种新的$1/(1-\rho)$尺度界。我们的界虽然限于轻尾情形及队列长度的一阶矩，但其主导常数更具可解释性，且通常更紧。证明过程相对简洁，运用了修正的$GI/GI/n$队列、二次测试函数的平稳性以及一种新颖的留一耦合技术。最后，我们还将该方法推广至服务时间分布完全异构的$GI/GI/n$队列。