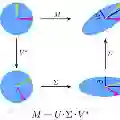
This paper is devoted to studying the application of the block Krylov subspace method for approximation of the truncated tensor SVD (T-SVD). The theoretical results of the proposed randomized approach are presented. Several experimental experiments using synthetics and real-world data are conducted to verify the efficiency and feasibility of the proposed randomized approach, and the numerical results show that the proposed method provides promising results. Applications of the proposed approach to data completion and data compression are presented.

翻译：本文致力于研究块Krylov子空间方法在截断张量奇异值分解近似中的应用。文中提出了所建议随机化方法的理论结果。通过使用合成数据与真实世界数据进行多组实验，验证了该随机化方法的效率与可行性，数值结果表明该方法能提供具有前景的计算结果。本文进一步展示了该方法在数据补全与数据压缩领域的应用实例。