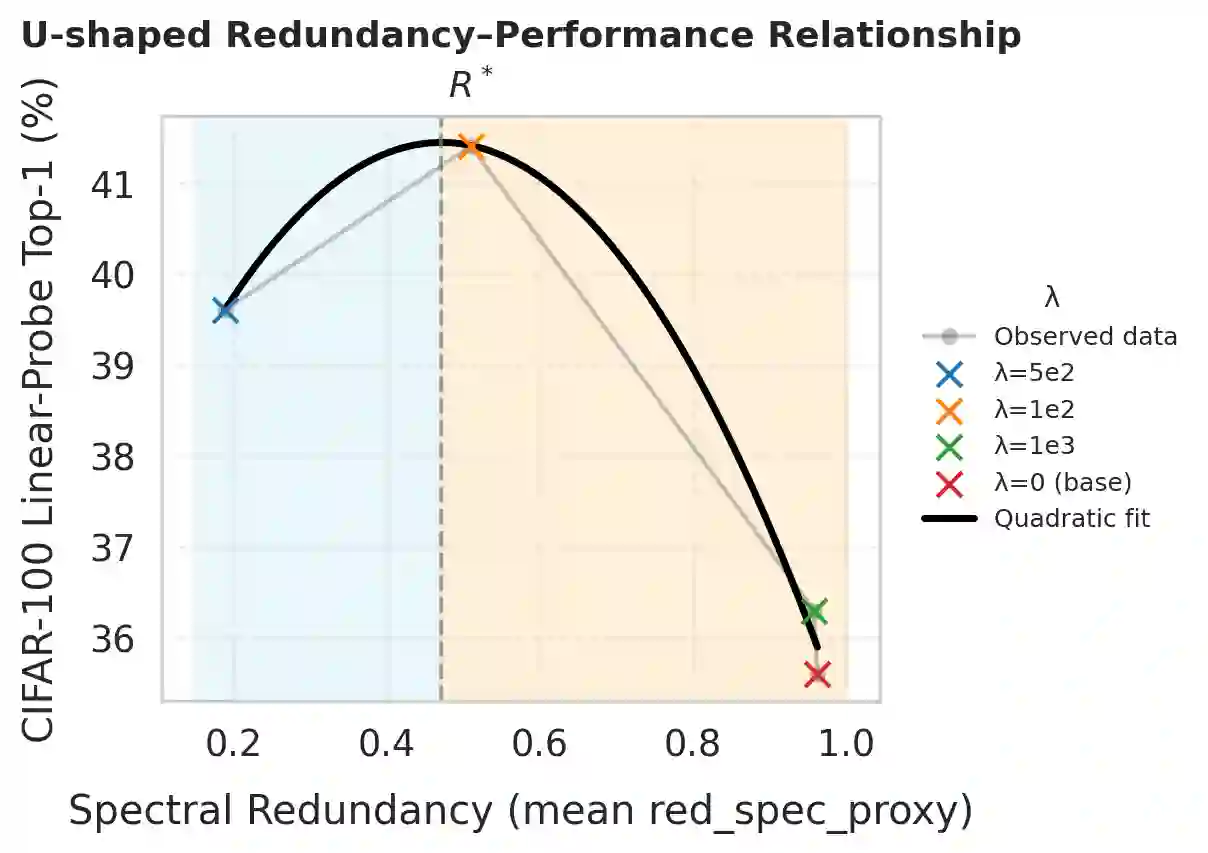
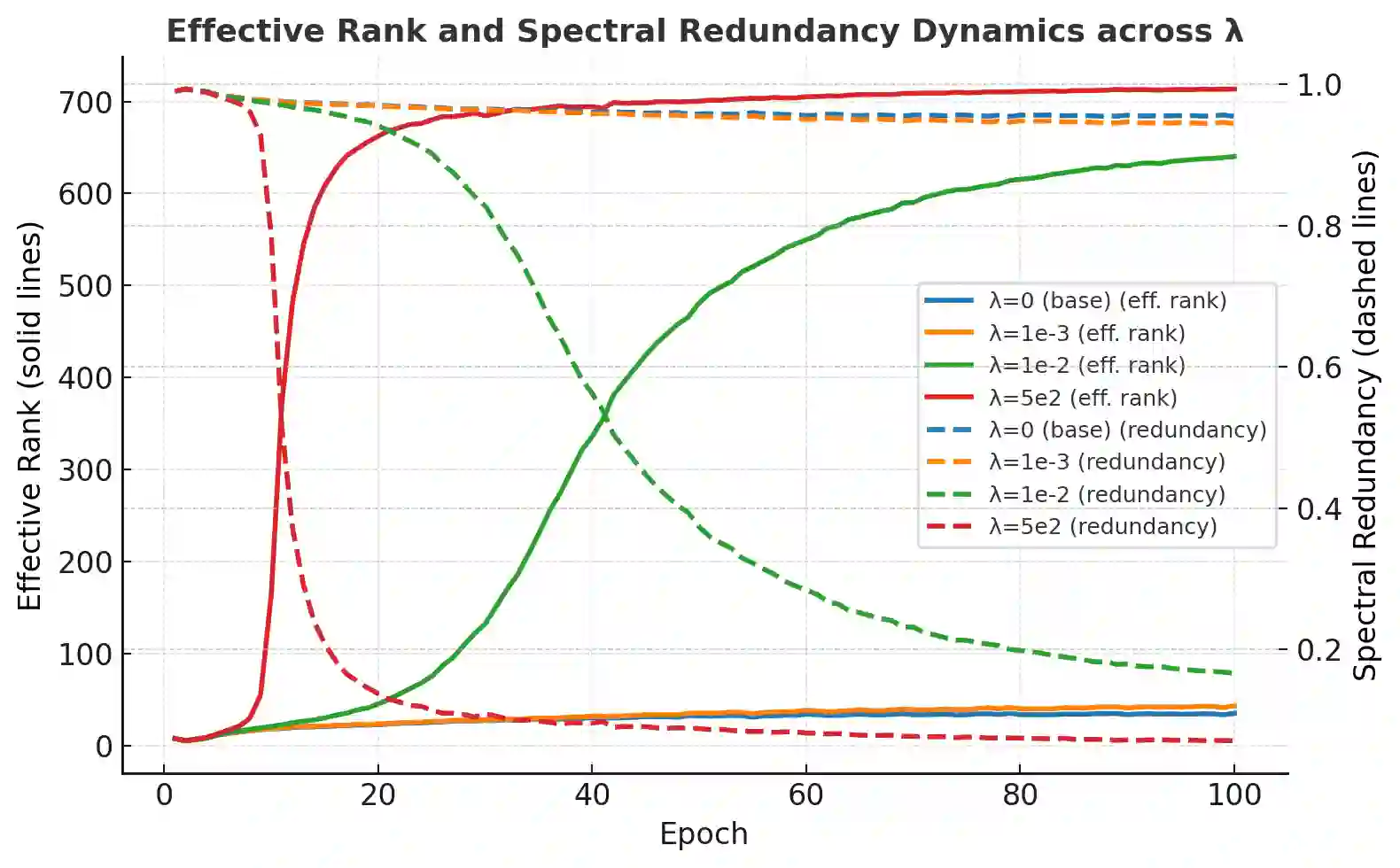
We present a theoretical framework that extends classical information theory to finite and structured systems by redefining redundancy as a fundamental property of information organization rather than inefficiency. In this framework, redundancy is expressed as a general family of informational divergences that unifies multiple classical measures, such as mutual information, chi-squared dependence, and spectral redundancy, under a single geometric principle. This reveals that these traditional quantities are not isolated heuristics but projections of a shared redundancy geometry. The theory further predicts that redundancy is bounded both above and below, giving rise to an optimal equilibrium that balances over-compression (loss of structure) and over-coupling (collapse). While classical communication theory favors minimal redundancy for transmission efficiency, finite and structured systems, such as those underlying real-world learning, achieve maximal stability and generalization near this equilibrium. Experiments with masked autoencoders are used to illustrate and verify this principle: the model exhibits a stable redundancy level where generalization peaks. Together, these results establish redundancy as a measurable and tunable quantity that bridges the asymptotic world of communication and the finite world of learning.

翻译：我们提出一个理论框架，通过将冗余重新定义为信息组织的基本属性而非低效表现，将经典信息论扩展至有限结构化系统。在此框架中，冗余被表达为一族广义的信息散度，该族散度将互信息、卡方依赖性和谱冗余等多种经典度量统一于单一几何原理之下。这表明这些传统量并非孤立的启发式度量，而是共享冗余几何结构的投影。该理论进一步预测冗余具有上下界，从而产生平衡过度压缩（结构丢失）与过度耦合（系统坍缩）的最优均衡点。虽然经典通信理论为追求传输效率倾向于最小化冗余，但现实世界学习所依托的有限结构化系统恰在此均衡点附近实现最大稳定性与泛化能力。我们通过掩码自编码器的实验阐释并验证该原理：模型在泛化能力达到峰值时呈现出稳定的冗余水平。这些成果共同确立了冗余作为一种可测量、可调节的量，架起了通信的渐近世界与学习的有限世界之间的桥梁。