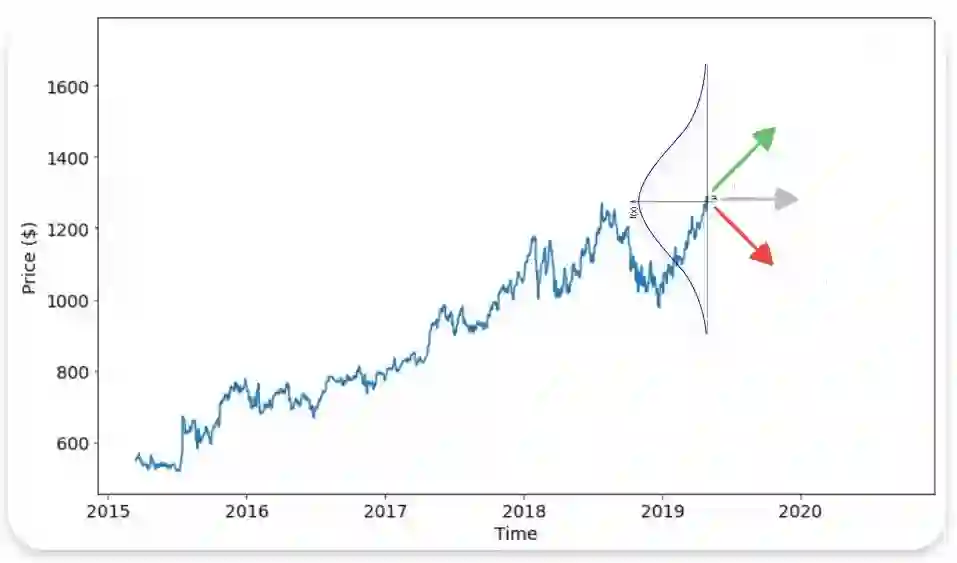
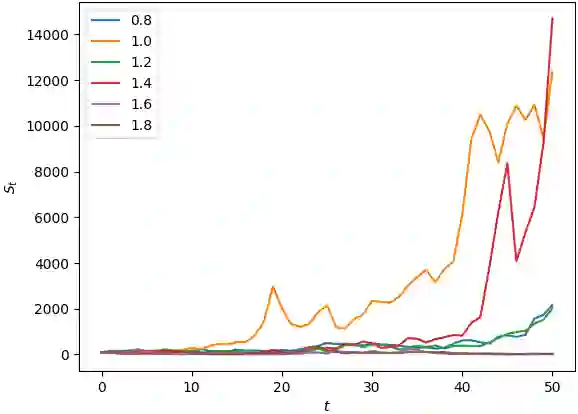
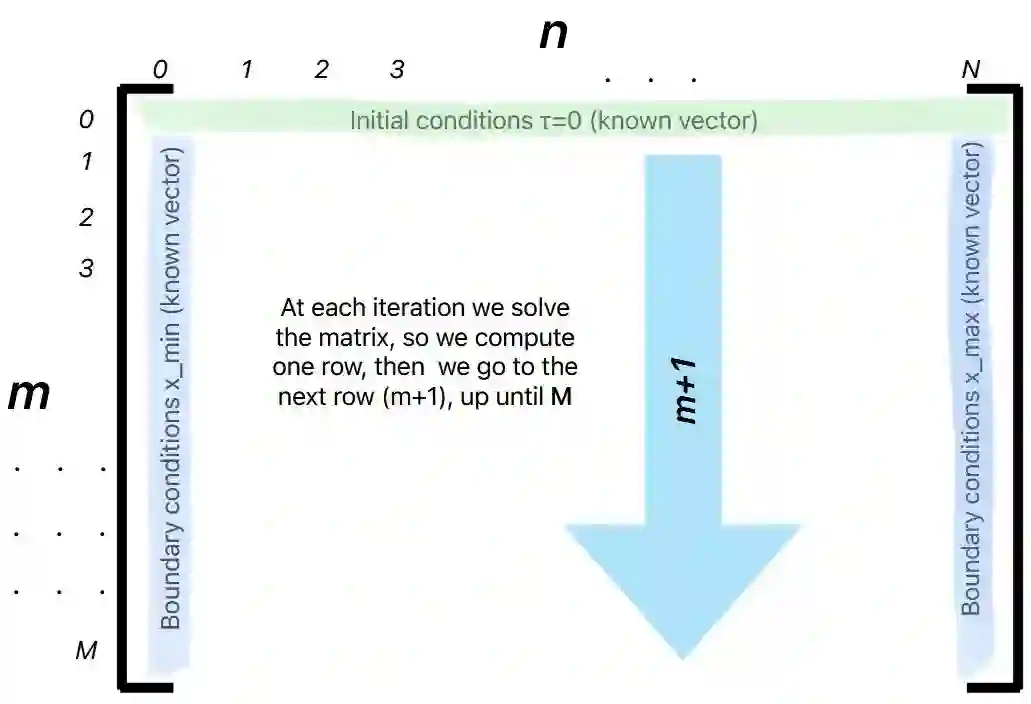
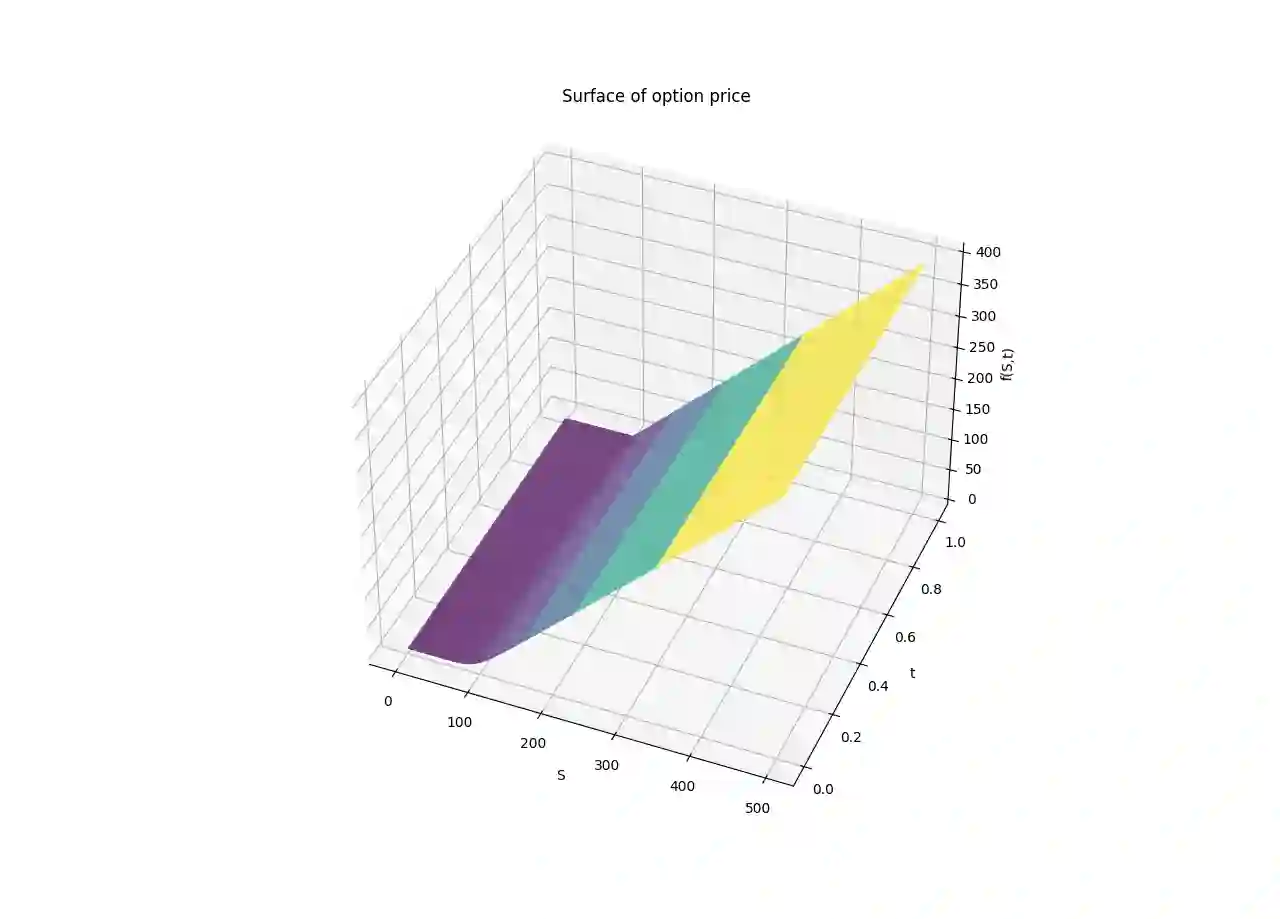
The main purpose of this article is to give a general overview and understanding of the first widely used option-pricing model, the Black-Scholes model. The history and context are presented, with the usefulness and implications in the economics world. A brief review of fundamental calculus concepts is introduced to derive and solve the model. The equation is then resolved using both an analytical (variable separation) and a numerical method (finite differences). Conclusions are drawn in order to understand how Black-Scholes is employed nowadays. At the end a handy appendix (A) is written with some economics notions to ease the reader's comprehension of the paper; furthermore a second appendix (B) is given with some code scripts, to allow the reader to put in practice some concepts.

翻译：本文的主要目的是对首个广泛应用的期权定价模型——布莱克-斯科尔斯模型进行系统性综述与阐释。文章首先介绍该模型的历史背景及其在经济学领域的重要意义与应用价值。通过回顾基础微积分概念，推导并求解该模型方程。随后分别采用解析方法（变量分离法）与数值方法（有限差分法）对模型方程进行求解。最后通过结论探讨布莱克-斯科尔斯模型在当代的实际应用模式。文末附有实用附录：附录（A）提供经济学基础概念以辅助读者理解全文；附录（B）则附有代码脚本，便于读者实践相关理论概念。