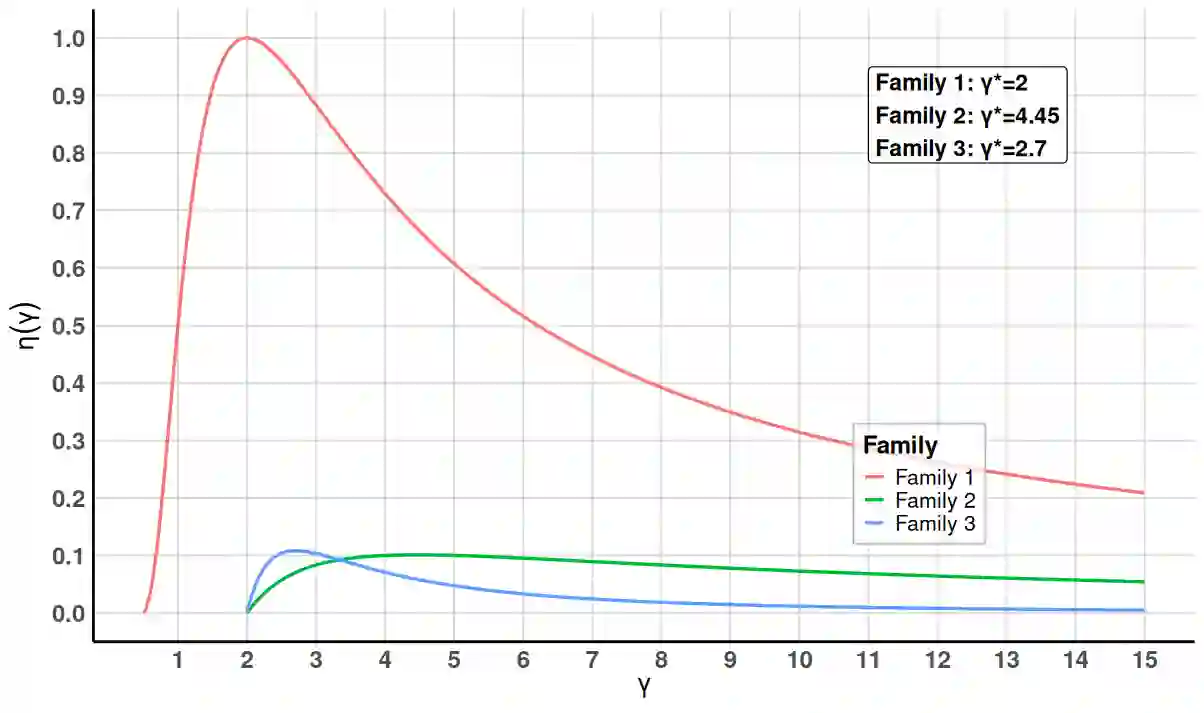
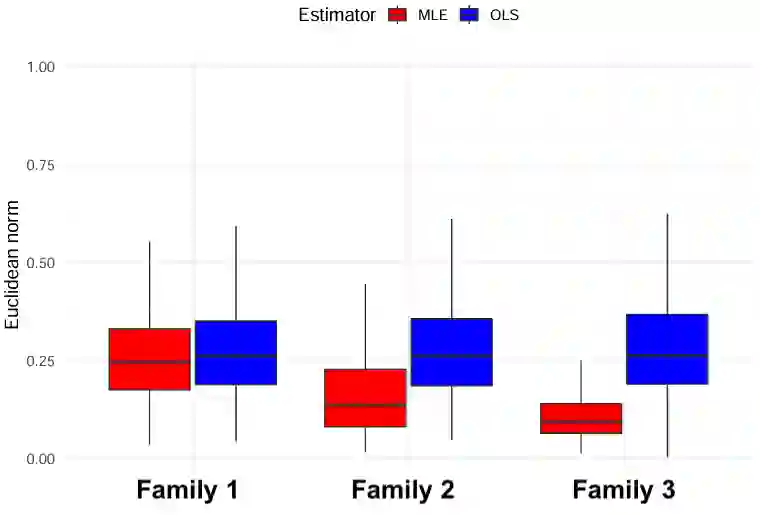
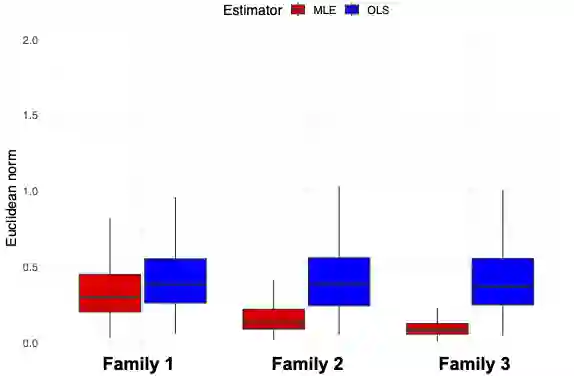
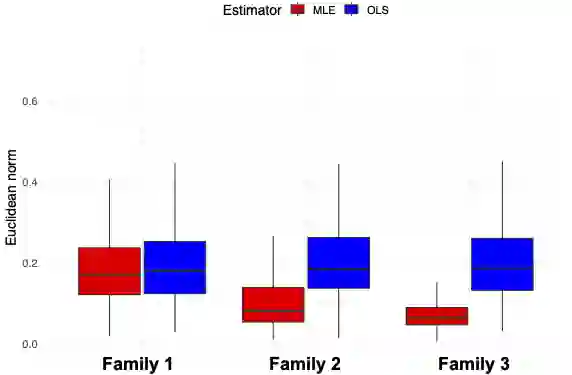
While the ordinary least squares estimator (OLSE) is still the most used estimator in linear regression models, other estimators can be more efficient when the error distribution is not Gaussian. In this paper, our goal is to evaluate this efficiency in the case of the Maximum Likelihood estimator (MLE) when the noise distribution belongs to a scale family. Under some regularity conditions, we show that (\beta_n,s_n), the MLE of the unknown regression vector \beta_0 and the scale s_0 exists and give the expression of the asymptotic efficiency of \beta_n over the OLSE. For given three scale families of densities, we quantify the true statistical gain of the MLE as a function of their deviation from the Gaussian family. To illustrate the theory, we present simulation results for different settings and also compare the MLE to the OLSE for the real market fish dataset.

翻译：尽管普通最小二乘估计器（OLSE）仍是线性回归模型中最常用的估计器，但当误差分布非高斯分布时，其他估计器可能具有更高的效率。本文旨在评估当噪声分布属于尺度分布族时，最大似然估计器（MLE）的效率。在一定的正则性条件下，我们证明了未知回归向量β₀和尺度参数s₀的最大似然估计(βₙ,sₙ)的存在性，并给出了βₙ相对于OLSE的渐近效率表达式。针对给定的三个尺度密度分布族，我们量化了MLE相对于高斯分布族的偏离程度所对应的实际统计增益。为验证理论，我们展示了不同设置下的模拟结果，并在真实市场鱼类数据集上比较了MLE与OLSE的性能。