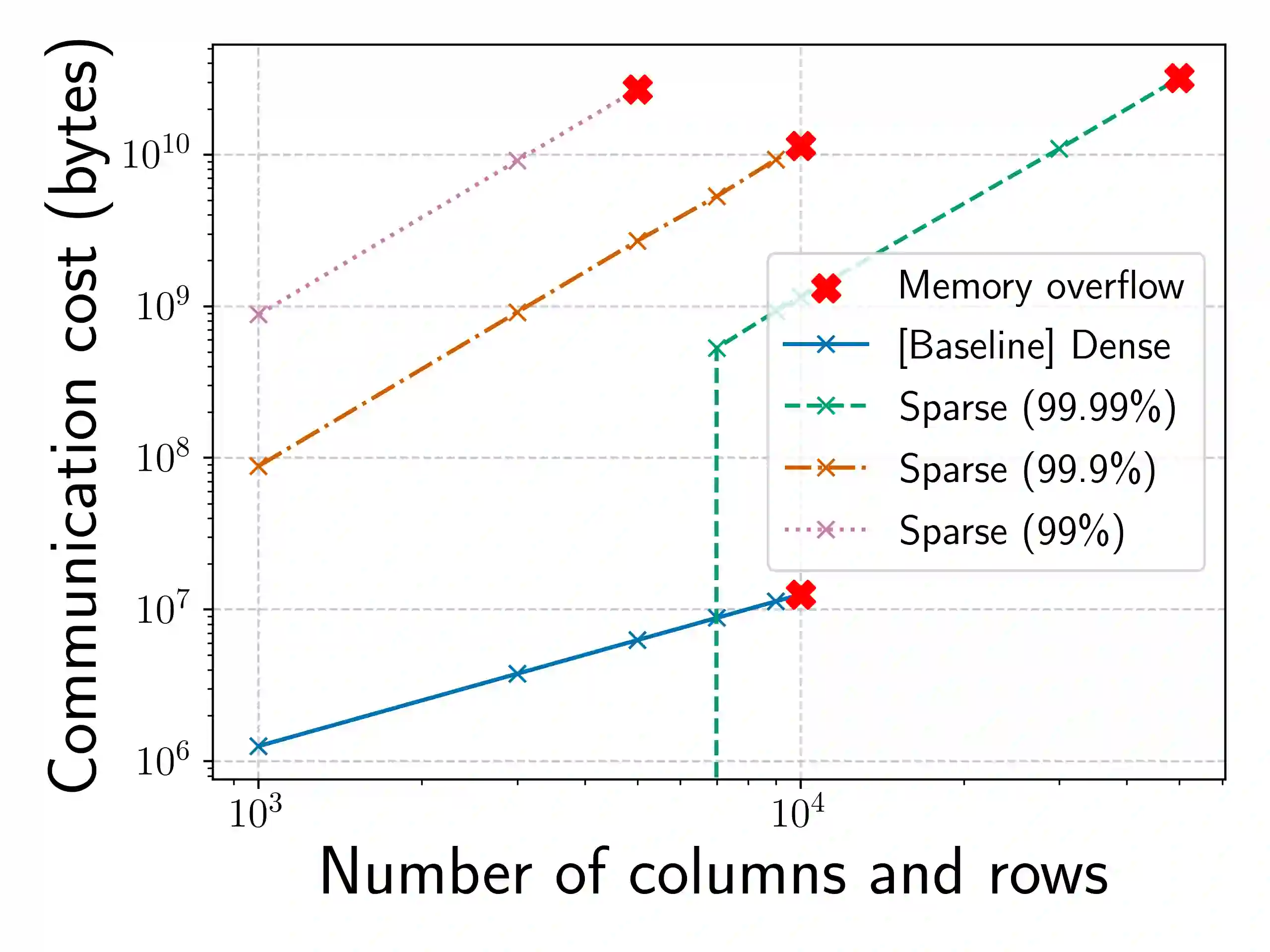
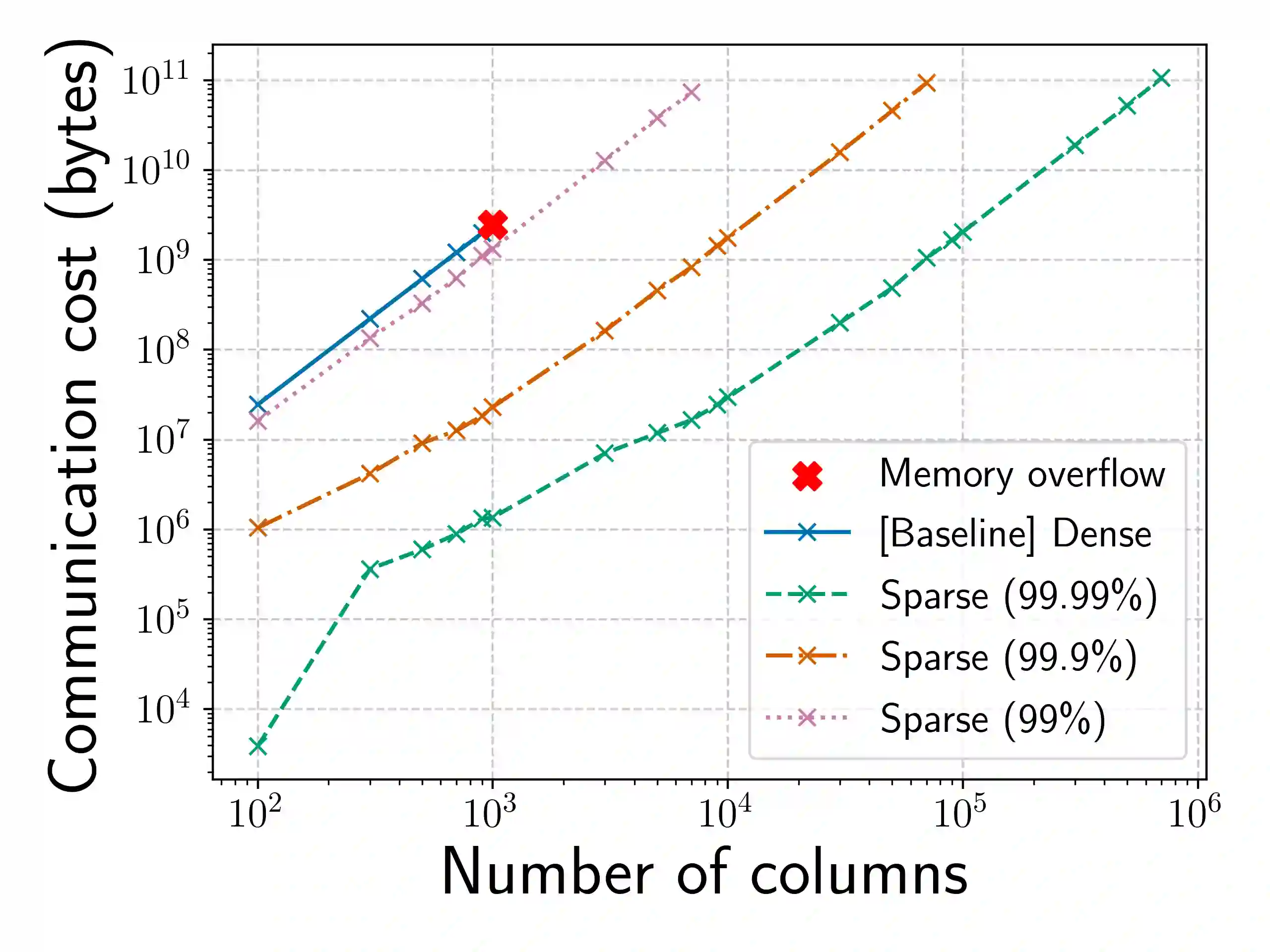
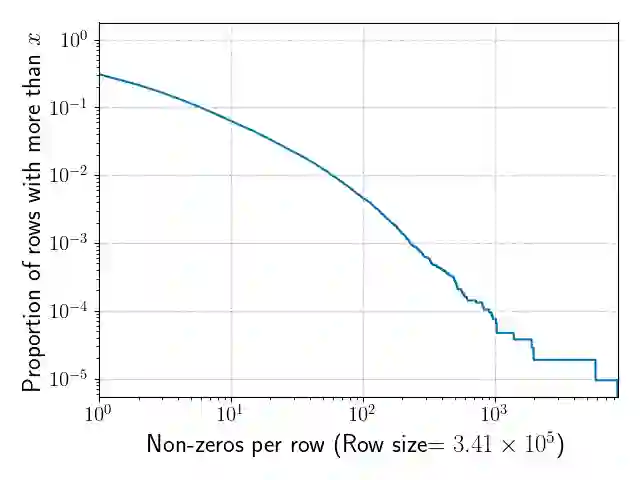
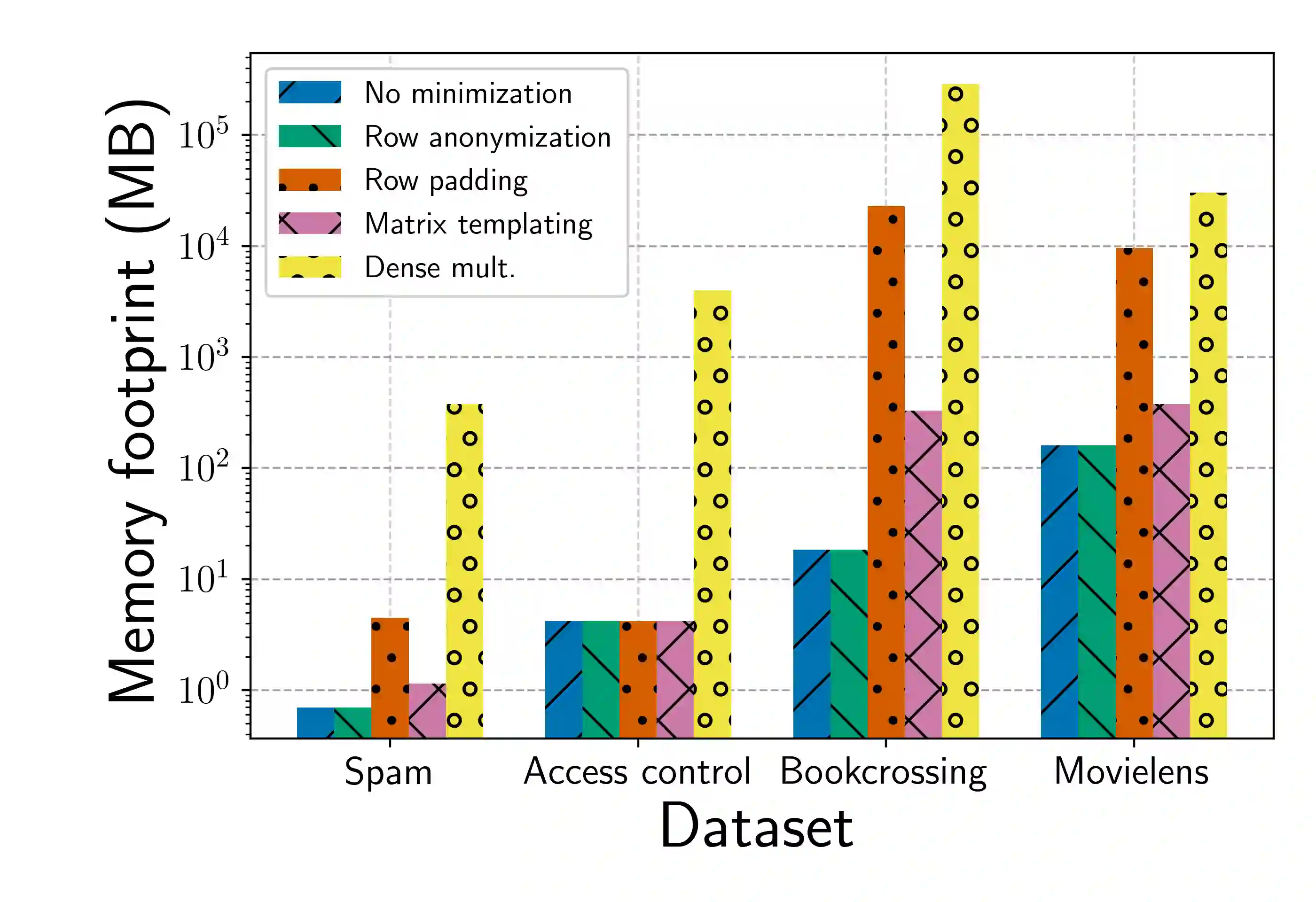
To preserve privacy, multi-party computation (MPC) enables executing Machine Learning (ML) algorithms on secret-shared or encrypted data. However, existing MPC frameworks are not optimized for sparse data. This makes them unsuitable for ML applications involving sparse data, e.g., recommender systems or genomics. Even in plaintext, such applications involve high-dimensional sparse data, that cannot be processed without sparsity-related optimizations due to prohibitively large memory requirements. Since matrix multiplication is central in ML algorithms, we propose MPC algorithms to multiply secret sparse matrices. On the one hand, our algorithms avoid the memory issues of the "dense" data representation of classic secure matrix multiplication algorithms. On the other hand, our algorithms can significantly reduce communication costs (some experiments show a factor 1000) for realistic problem sizes. We validate our algorithms in two ML applications in which existing protocols are impractical. An important question when developing MPC algorithms is what assumptions can be made. In our case, if the number of non-zeros in a row is a sensitive piece of information then a short runtime may reveal that the number of non-zeros is small. Existing approaches make relatively simple assumptions, e.g., that there is a universal upper bound to the number of non-zeros in a row. This often doesn't align with statistical reality, in a lot of sparse datasets the amount of data per instance satisfies a power law. We propose an approach which allows adopting a safe upper bound on the distribution of non-zeros in rows/columns of sparse matrices.

翻译：为保护隐私，多方计算（MPC）使得能够在秘密共享或加密数据上执行机器学习（ML）算法。然而，现有MPC框架未针对稀疏数据进行优化，导致其不适用于涉及稀疏数据的ML应用（如推荐系统或基因组学）。即使在明文状态下，此类应用也涉及高维稀疏数据，若无稀疏性相关优化则因内存需求过大而无法处理。鉴于矩阵乘法在ML算法中的核心地位，我们提出了用于秘密稀疏矩阵相乘的MPC算法。一方面，我们的算法避免了经典安全矩阵乘法算法中“稠密”数据表示的内存问题；另一方面，对于实际规模的问题，我们的算法能显著降低通信成本（部分实验显示可达1000倍）。我们在两个现有协议不实用的ML应用中验证了算法性能。开发MPC算法时的重要问题是可作何种假设：若行中非零元素数量属于敏感信息，则较短的运行时间可能揭示非零元素数量较少。现有方法采用相对简单的假设（例如行非零元素数量存在通用上界），但这常与统计现实不符——许多稀疏数据集中每个实例的数据量符合幂律分布。我们提出了一种方法，允许对稀疏矩阵行/列中非零元素分布采用安全上界。