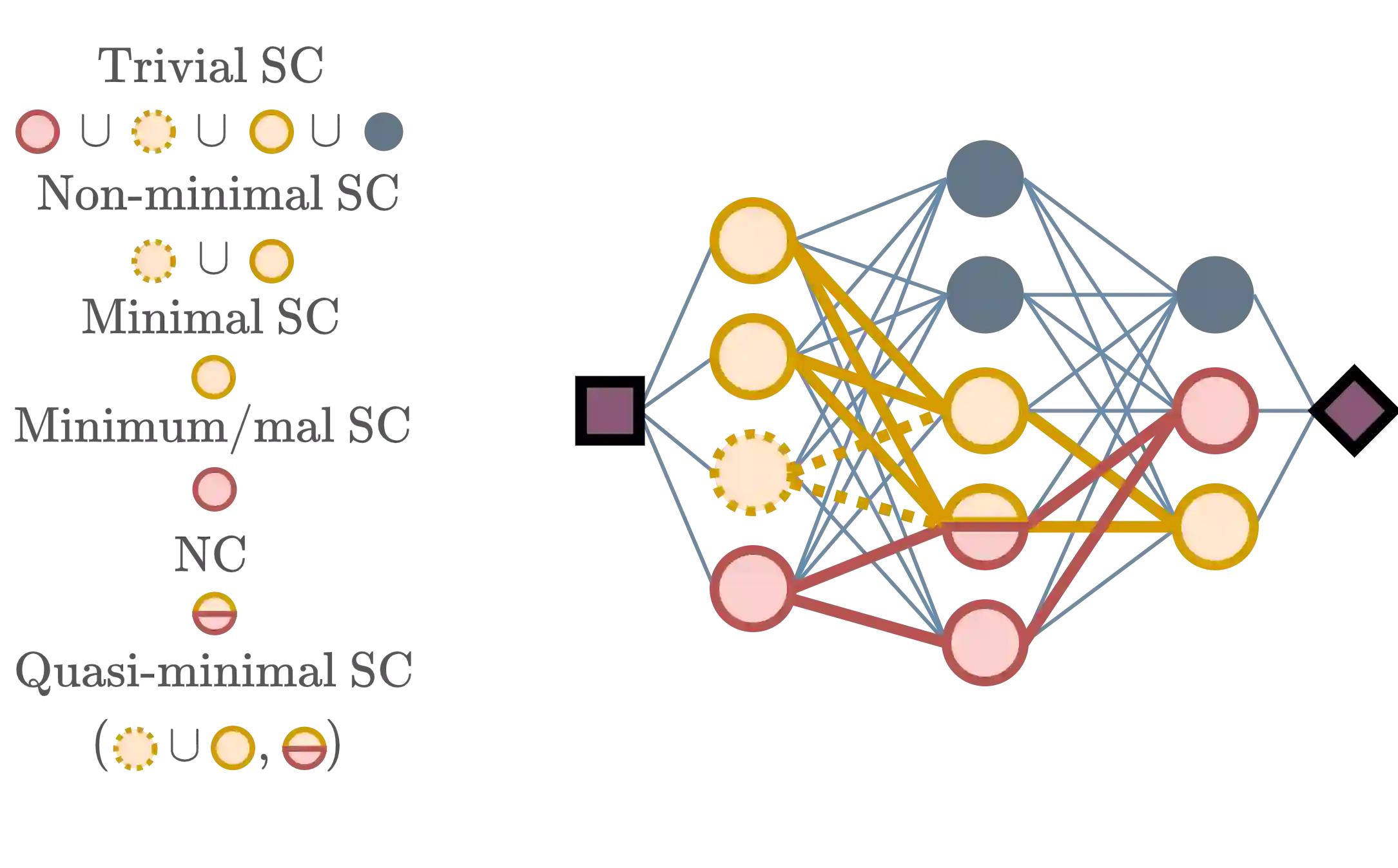
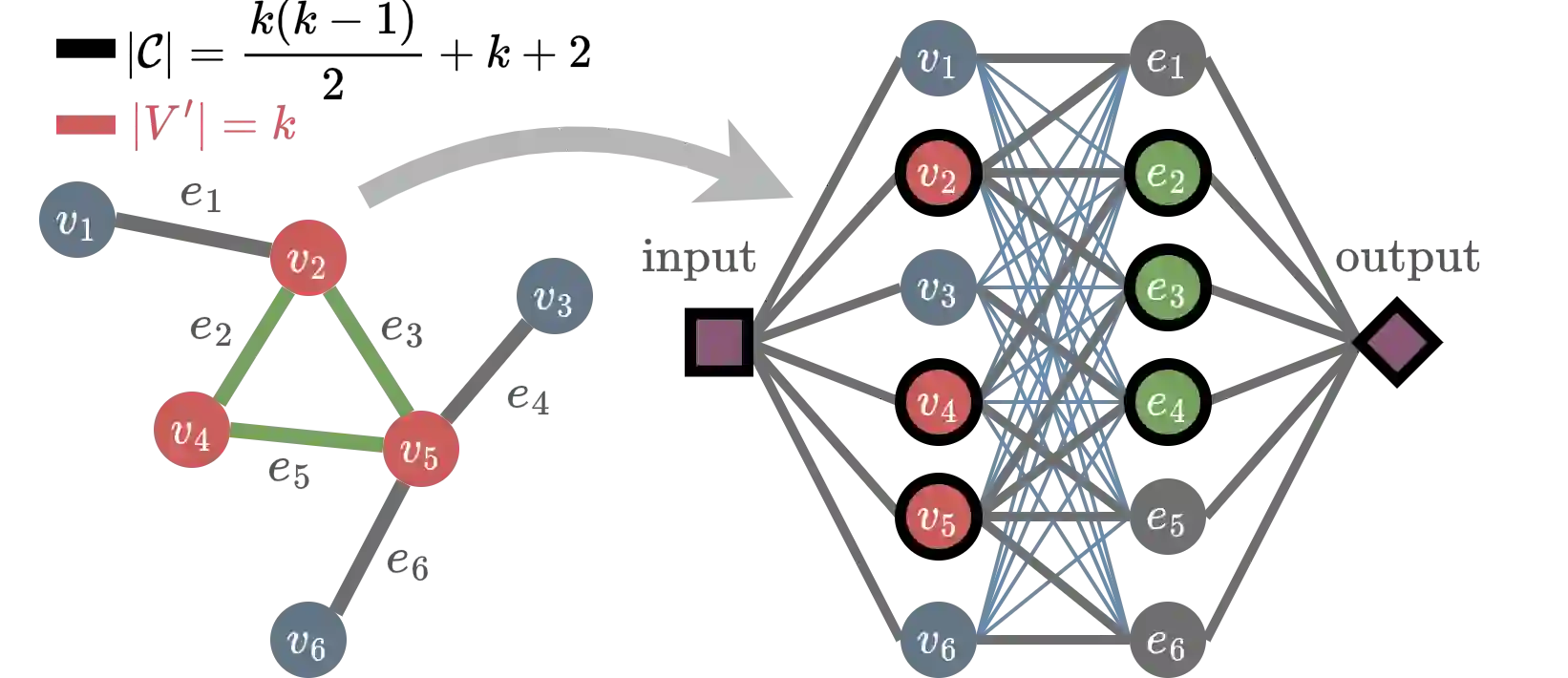
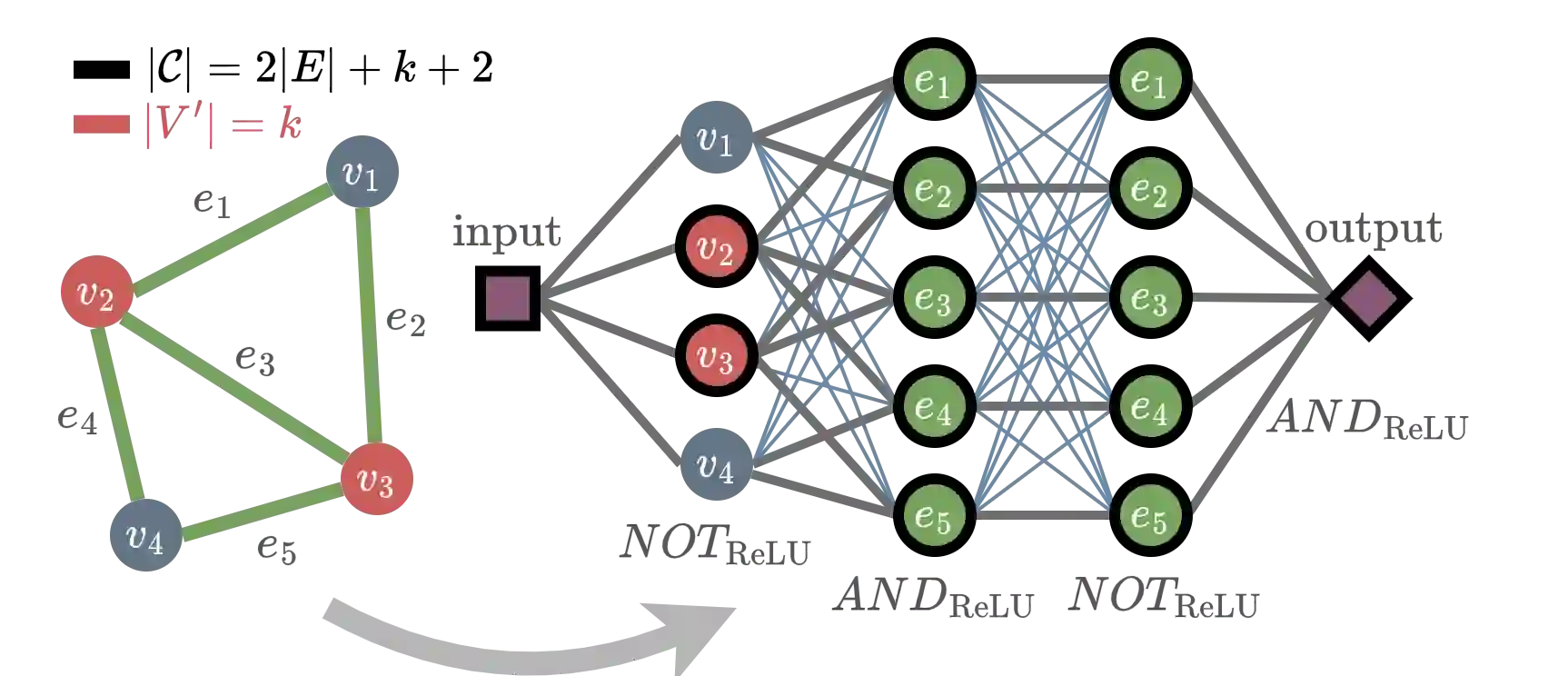
Many proposed applications of neural networks in machine learning, cognitive/brain science, and society hinge on the feasibility of inner interpretability via circuit discovery. This calls for empirical and theoretical explorations of viable algorithmic options. Despite advances in the design and testing of heuristics, there are concerns about their scalability and faithfulness at a time when we lack understanding of the complexity properties of the problems they are deployed to solve. To address this, we study circuit discovery with classical and parameterized computational complexity theory: (1) we describe a conceptual scaffolding to reason about circuit finding queries in terms of affordances for description, explanation, prediction and control; (2) we formalize a comprehensive set of queries for mechanistic explanation, and propose a formal framework for their analysis; (3) we use it to settle the complexity of many query variants and relaxations of practical interest on multi-layer perceptrons. Our findings reveal a challenging complexity landscape. Many queries are intractable, remain fixed-parameter intractable relative to model/circuit features, and inapproximable under additive, multiplicative, and probabilistic approximation schemes. To navigate this landscape, we prove there exist transformations to tackle some of these hard problems with better-understood heuristics, and prove the tractability or fixed-parameter tractability of more modest queries which retain useful affordances. This framework allows us to understand the scope and limits of interpretability queries, explore viable options, and compare their resource demands on existing and future architectures.

翻译：在机器学习、认知/脑科学以及社会应用中，许多神经网络应用方案的成功实施依赖于通过电路发现实现内可解释性的可行性。这要求我们对可行的算法选择进行实证与理论探索。尽管启发式方法的设计与测试已取得进展，但在当前对求解问题复杂性缺乏理解的情况下，其可扩展性与保真度仍令人担忧。为此，我们运用经典与参数化计算复杂性理论研究电路发现问题：(1) 构建概念框架，从描述、解释、预测与控制的功能支持角度分析电路查找查询；(2) 形式化一组完整的机制解释查询，并提出其分析的形式框架；(3) 利用该框架确定多层感知机上多种实用查询变体及松弛形式的复杂性。研究结果揭示了极具挑战性的复杂性图景：多数查询具有难解性，且相对于模型/电路特征保持固定参数难解性，在加性、乘性及概率近似方案下均不可近似。为应对此挑战，我们证明存在可通过更成熟启发式方法处理部分难题的转化方法，并证实保留实用功能支持的适度查询具有可解性或固定参数可解性。该框架有助于理解可解释性查询的适用范围与局限，探索可行方案，并比较其在现有及未来架构上的资源需求。