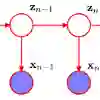
Hidden Markov models (HMMs) have been used increasingly to understand how movement patterns of animals arise from behavioural states. An animal is assumed to transition between behavioural states through time, as described by transition probabilities. Within each state, the movement typically follows a discrete-time random walk, where steps between successive observed locations are described in terms of step lengths (related to speed) and turning angles (related to tortuosity). HMMs are discrete-time models, and most of their outputs strongly depend on the temporal resolution of data. We compile known theoretical results about scale dependence in Markov chains and correlated random walks, which are the most common components of HMMs for animal movement. We also illustrate this phenomenon using simulations covering a wide range of biological scenarios. The scale dependence affects not only all model parameters, i.e., the transition probabilities and the movement parameters within each behavioural state, but also the overall classification of movement patterns into states. This highlights the importance of carefully considering the time resolution when drawing conclusions from the results of analysis. In addition, scale dependence generally precludes the analysis of tracking data collected at irregular time intervals, and the comparison (or combination) of data sets with different sampling rates. HMMs remain a valuable tool to answer questions about animal movement and behaviour, as long as these limitations are well understood.

翻译：隐马尔可夫模型（HMMs）已越来越多地用于理解动物运动模式如何源于行为状态。假设动物随时间在行为状态之间转换，这种转换由转移概率描述。在每个状态内，运动通常遵循离散时间随机游走，其中连续观测位置之间的步长（与速度相关）和转向角（与曲折度相关）被用于描述步进过程。HMMs是离散时间模型，其大多数输出结果强烈依赖于数据的时间分辨率。我们汇编了关于马尔可夫链和相关随机游走中尺度依赖性的已知理论结果，这些是动物运动HMMs中最常见的组成部分。我们还通过模拟覆盖广泛的生物场景来说明这一现象。尺度依赖性不仅影响所有模型参数（即转移概率和各行为状态内的运动参数），还影响将运动模式整体分类为状态的结果。这凸显了在从分析结果中得出结论时，仔细考虑时间分辨率的重要性。此外，尺度依赖性通常排除了对不规则时间间隔收集的追踪数据的分析，以及不同采样率数据集之间的比较（或合并）。只要充分理解这些局限性，HMMs仍然是回答动物运动和行为相关问题的有力工具。