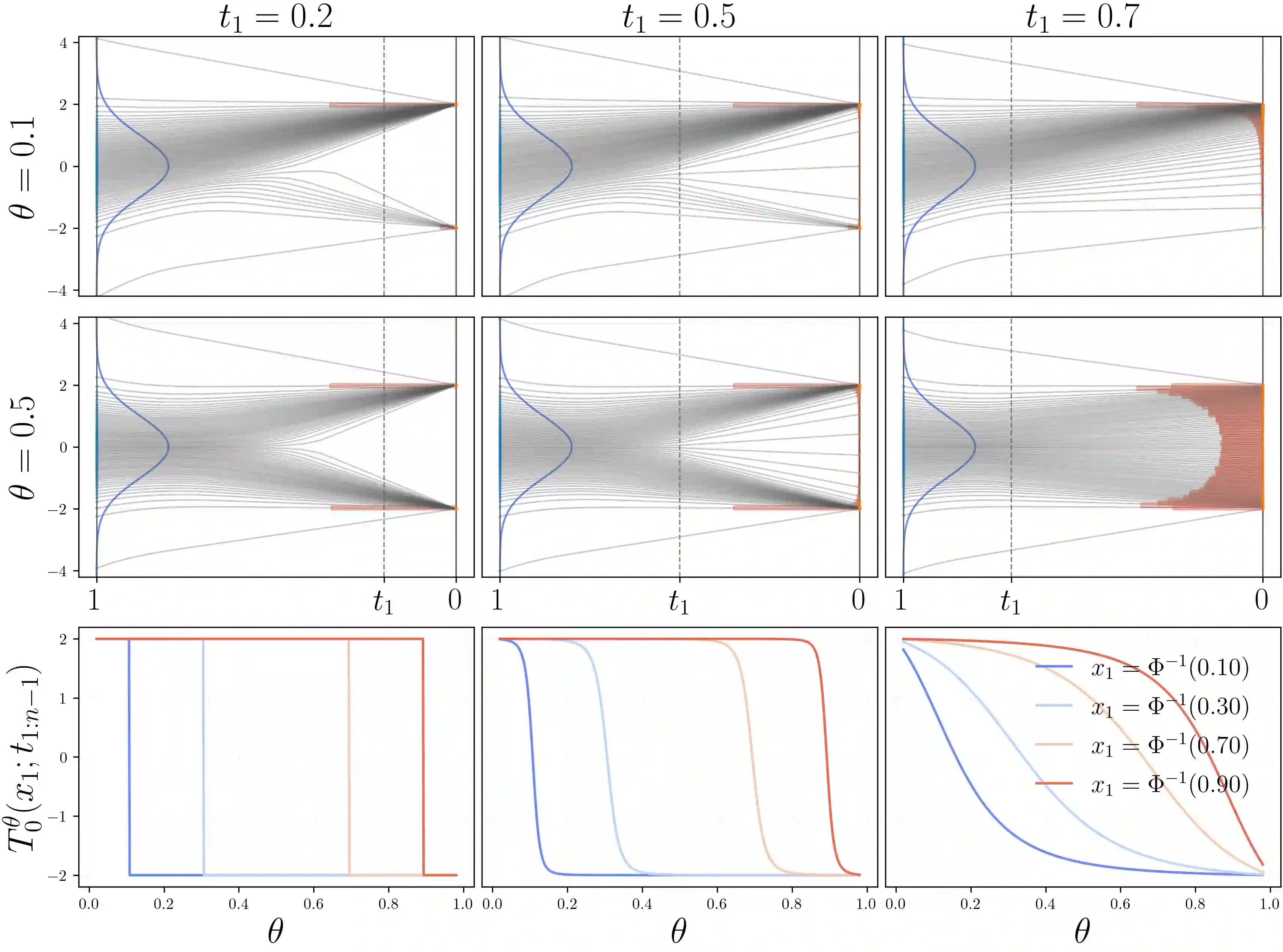
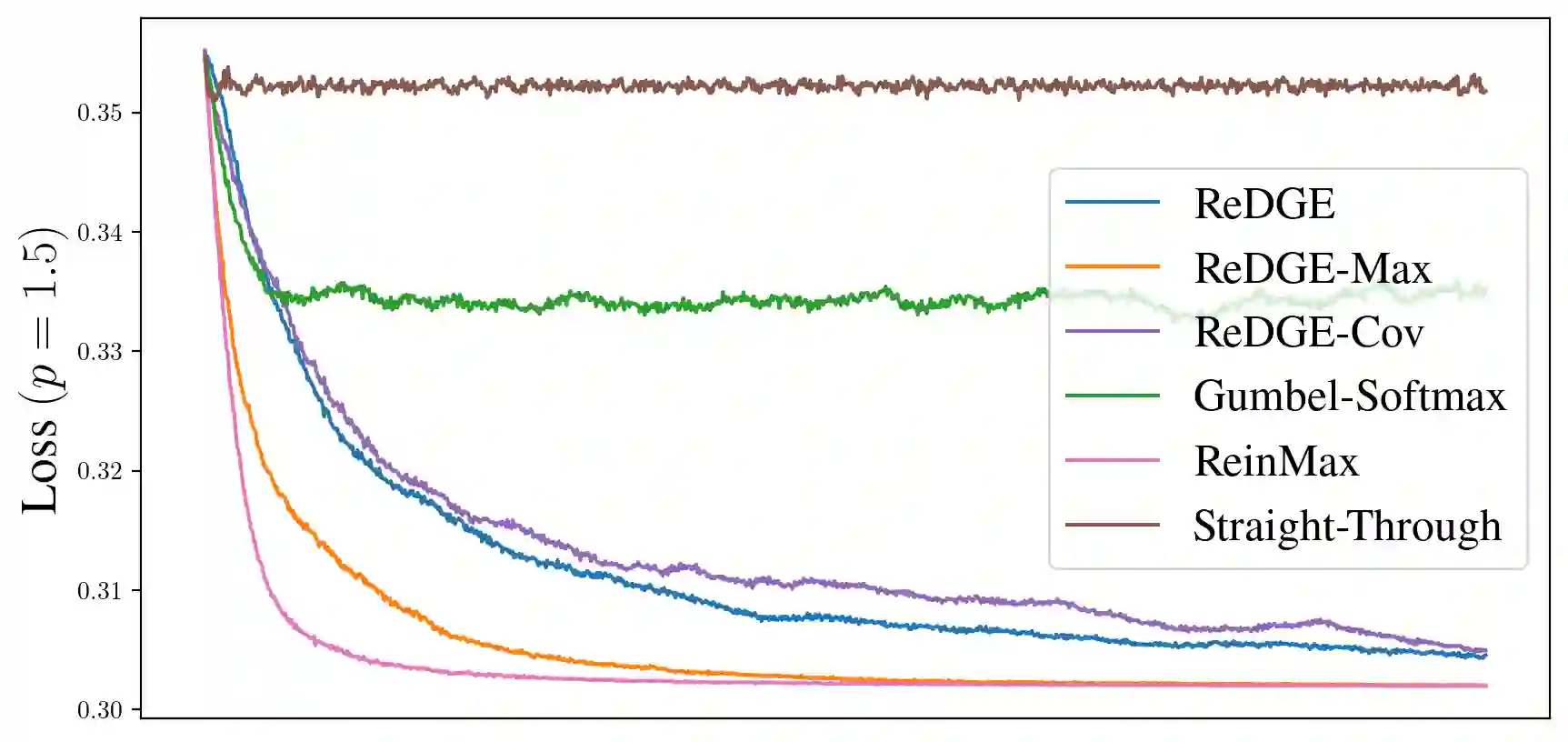
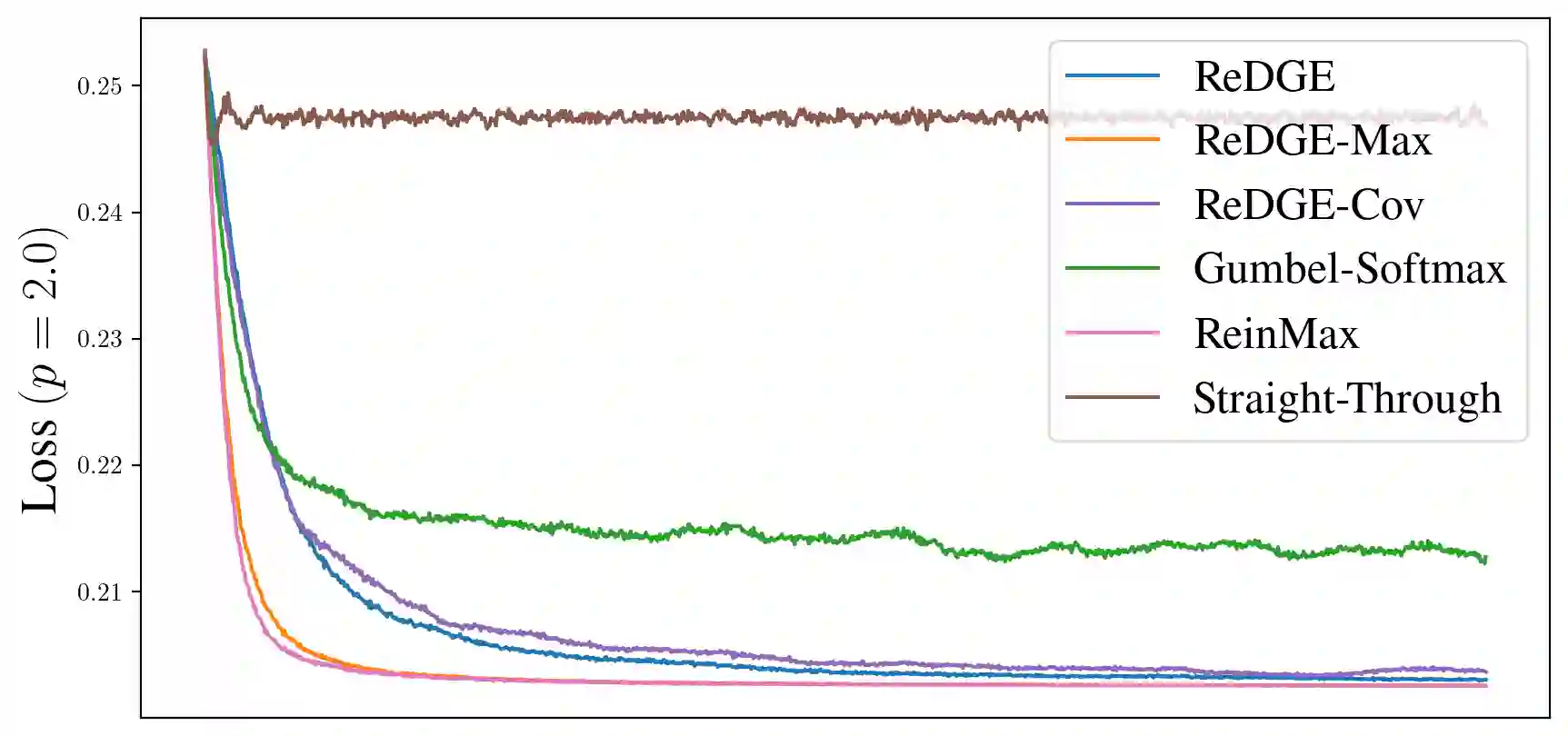
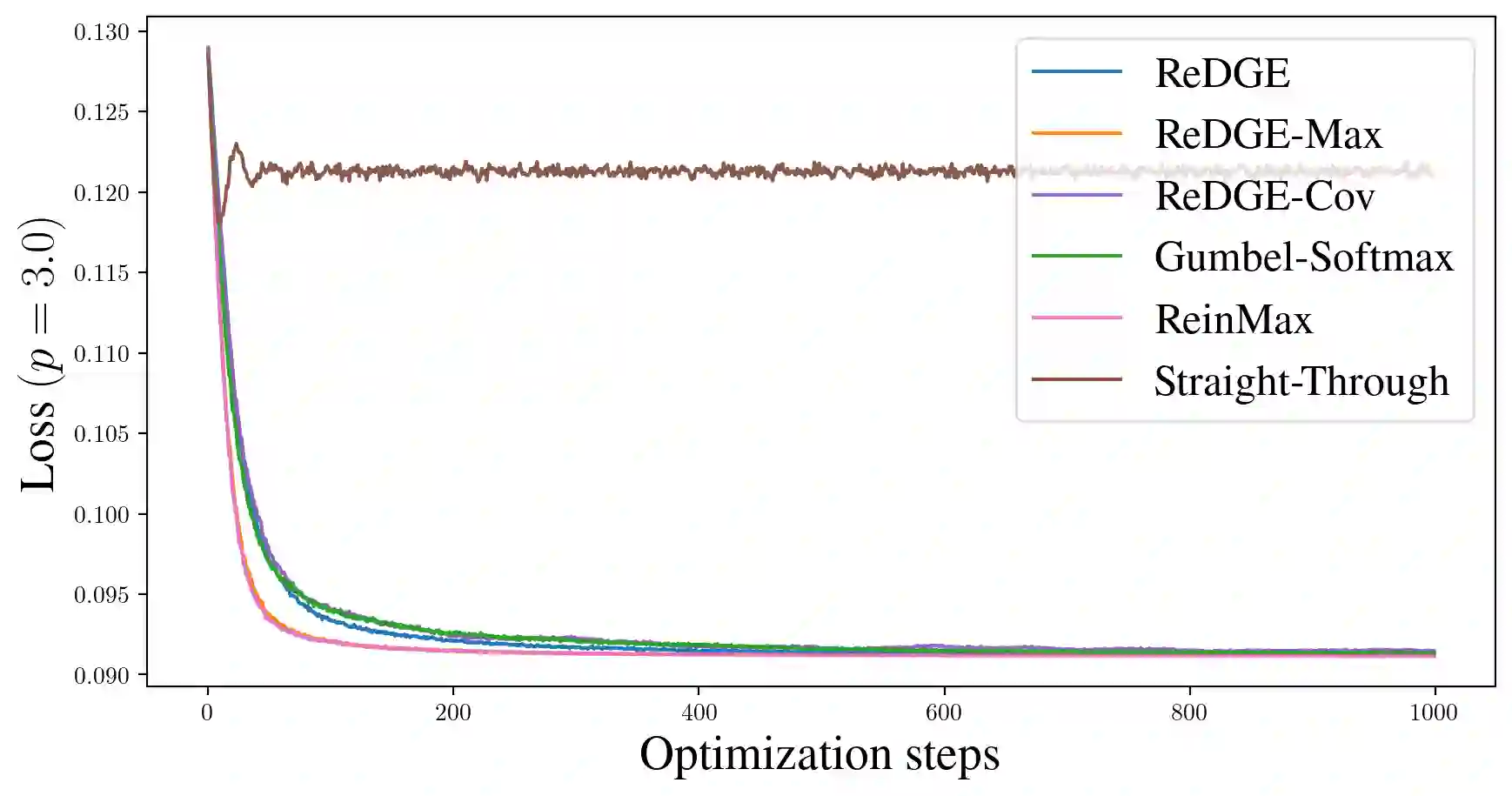
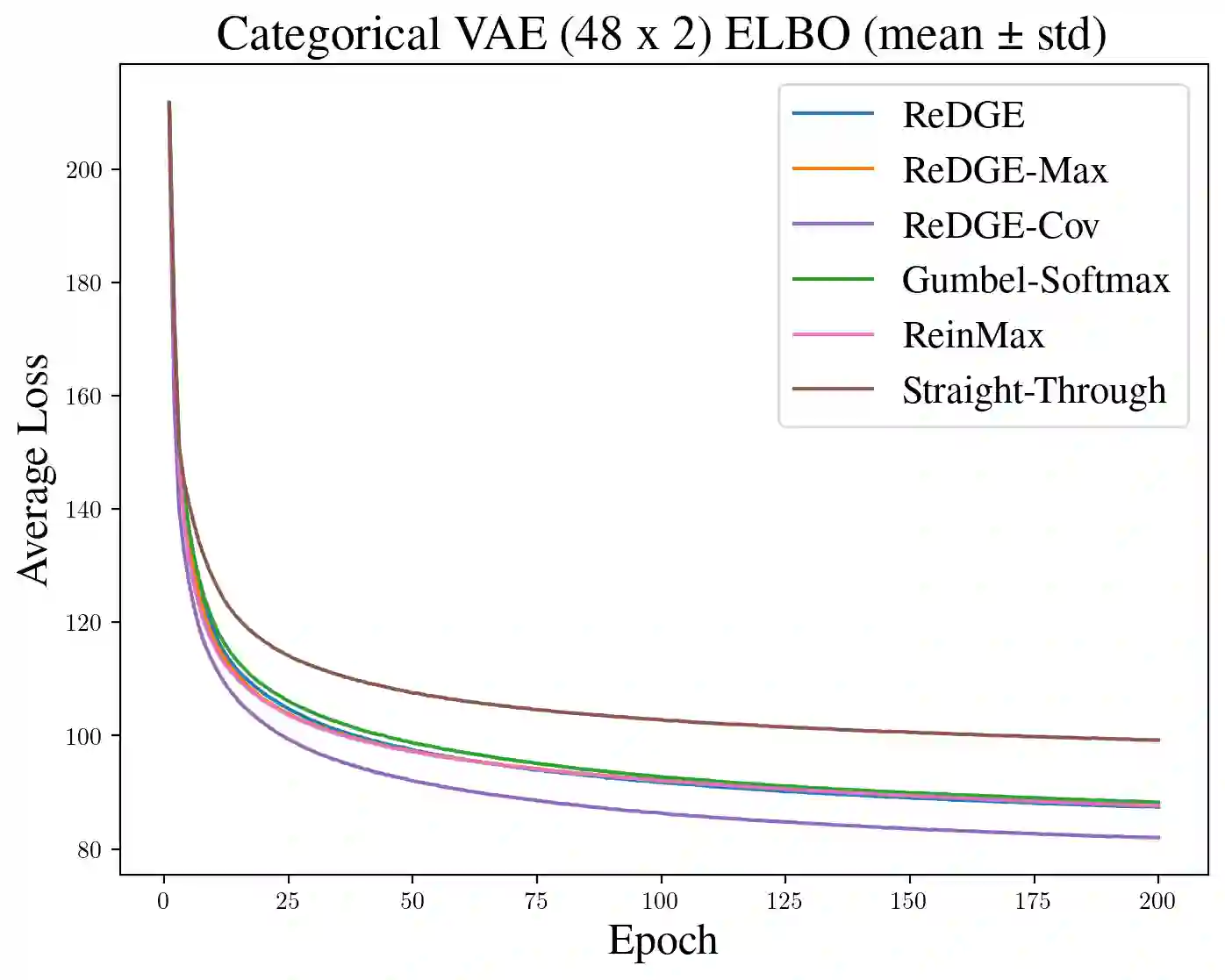
Gradient-based optimization with categorical variables typically relies on score-function estimators, which are unbiased but noisy, or on continuous relaxations that replace the discrete distribution with a smooth surrogate admitting a pathwise (reparameterized) gradient, at the cost of optimizing a biased, temperature-dependent objective. In this paper, we extend this family of relaxations by introducing a diffusion-based soft reparameterization for categorical distributions. For these distributions, the denoiser under a Gaussian noising process admits a closed form and can be computed efficiently, yielding a training-free diffusion sampler through which we can backpropagate. Our experiments show that the proposed reparameterization trick yields competitive or improved optimization performance on various benchmarks.

翻译：基于梯度的分类变量优化通常依赖于分数函数估计器，这类估计器虽无偏但噪声较大；或者依赖于连续松弛方法，即用平滑代理替代离散分布以获得路径式（重参数化）梯度，但代价是优化一个具有偏差且依赖温度的目标函数。本文通过引入一种基于扩散的软重参数化方法，扩展了此类松弛技术对分类分布的适用性。对于这类分布，高斯加噪过程下的去噪器具有闭式解且可高效计算，从而得到一个无需训练的扩散采样器，并支持反向传播。实验表明，所提出的重参数化技巧在多种基准测试中实现了具有竞争力或更优的优化性能。