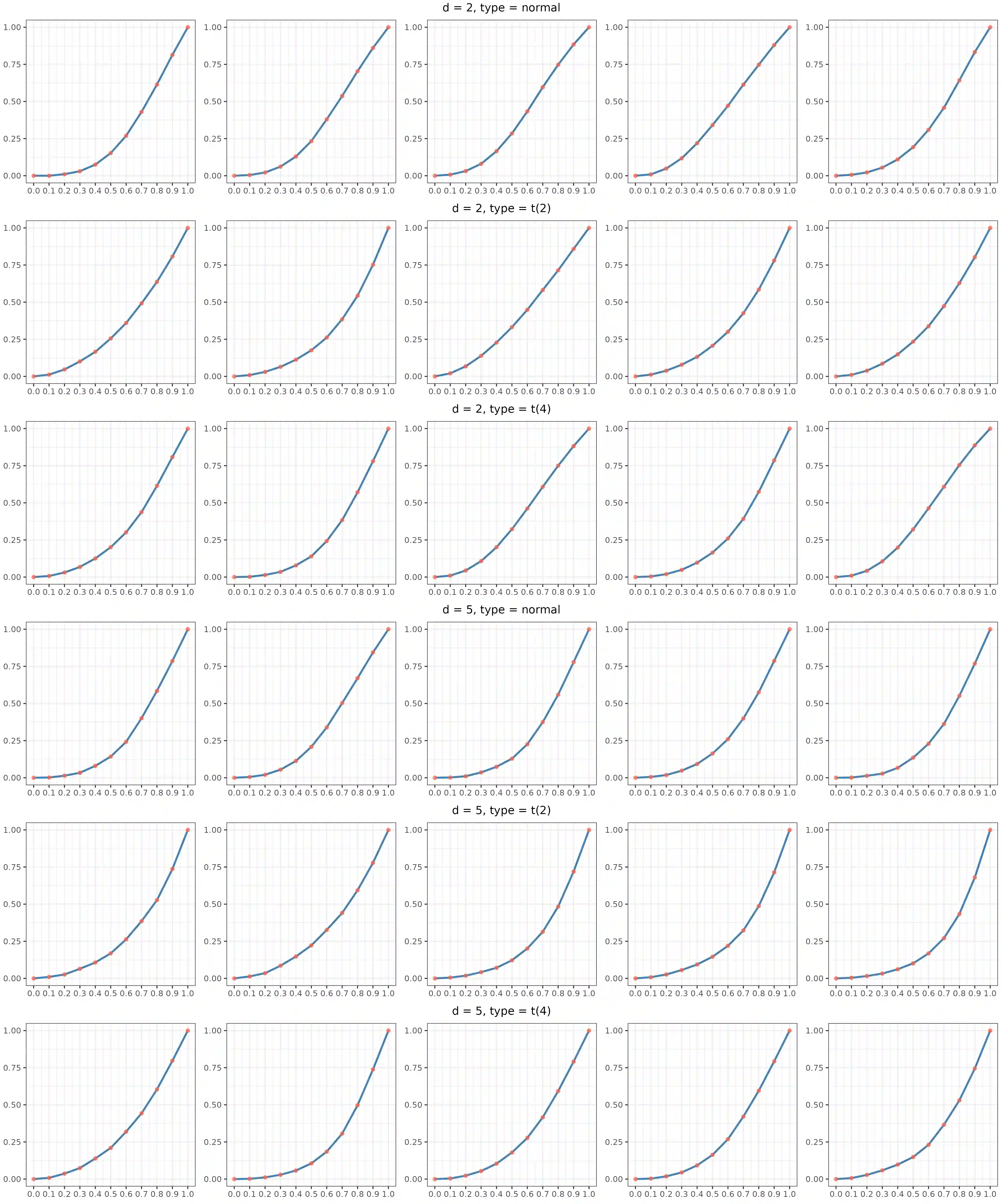
The Azadkia-Chatterjee coefficient is a rank-based measure of dependence between a random variable $Y \in \mathbb{R}$ and a random vector ${\boldsymbol Z} \in \mathbb{R}^{d_Z}$. In this paper, we propose a multivariate extension that measures the dependence between random vectors ${\boldsymbol Y} \in \mathbb{R}^{d_Y}$ and ${\boldsymbol Z} \in \mathbb{R}^{d_Z}$, based on $n$ i.i.d. samples. The proposed coefficient converges almost surely to a limit with the following properties: i) it lies in $[0, 1]$; ii) it is equal to zero if and only if ${\boldsymbol Y}$ and ${\boldsymbol Z}$ are independent; and iii) it is equal to one if and only if ${\boldsymbol Y}$ is almost surely a function of ${\boldsymbol Z}$. Remarkably, the only assumption required by this convergence is that ${\boldsymbol Y}$ is not almost surely a constant vector. We further prove that under the same mild condition and after a proper scaling, this coefficient converges in distribution to a standard normal random variable when ${\boldsymbol Y}$ and ${\boldsymbol Z}$ are independent. This asymptotic normality result allows us to construct a Wald-type hypothesis test of independence based on this coefficient. To compute this coefficient, we propose a merge sort based algorithm that runs in $O(n (\log n)^{d_Y})$. Finally, we show that it can be used to measure the conditional dependence between ${\boldsymbol Y}$ and ${\boldsymbol Z}$ conditional on a third random vector ${\boldsymbol X}$, and prove that the measure is monotonic with respect to the deviation from an independence distribution under certain model restrictions.

翻译：Azadkia-Chatterjee系数是一种基于秩的度量，用于衡量随机变量$Y \in \mathbb{R}$与随机向量${\boldsymbol Z} \in \mathbb{R}^{d_Z}$之间的依赖性。本文提出一种多元推广，基于$n$个独立同分布样本，用于度量随机向量${\boldsymbol Y} \in \mathbb{R}^{d_Y}$与${\boldsymbol Z} \in \mathbb{R}^{d_Z}$之间的依赖性。所提出的系数几乎必然收敛于一个具有以下性质的极限：i) 其值位于$[0, 1]$区间内；ii) 当且仅当${\boldsymbol Y}$与${\boldsymbol Z}$独立时，其值为零；iii) 当且仅当${\boldsymbol Y}$几乎必然是${\boldsymbol Z}$的函数时，其值为一。值得注意的是，该收敛所需的唯一假设是${\boldsymbol Y}$不是几乎必然的常向量。我们进一步证明，在相同的温和条件下，经过适当缩放后，当${\boldsymbol Y}$与${\boldsymbol Z}$独立时，该系数依分布收敛于标准正态随机变量。这一渐近正态性结果使我们能够基于该系数构建Wald型独立性假设检验。为计算该系数，我们提出了一种基于归并排序的算法，其时间复杂度为$O(n (\log n)^{d_Y})$。最后，我们展示了该系数可用于度量在给定第三个随机向量${\boldsymbol X}$的条件下${\boldsymbol Y}$与${\boldsymbol Z}$的条件依赖性，并证明在某些模型约束下，该度量相对于独立性分布的偏离具有单调性。