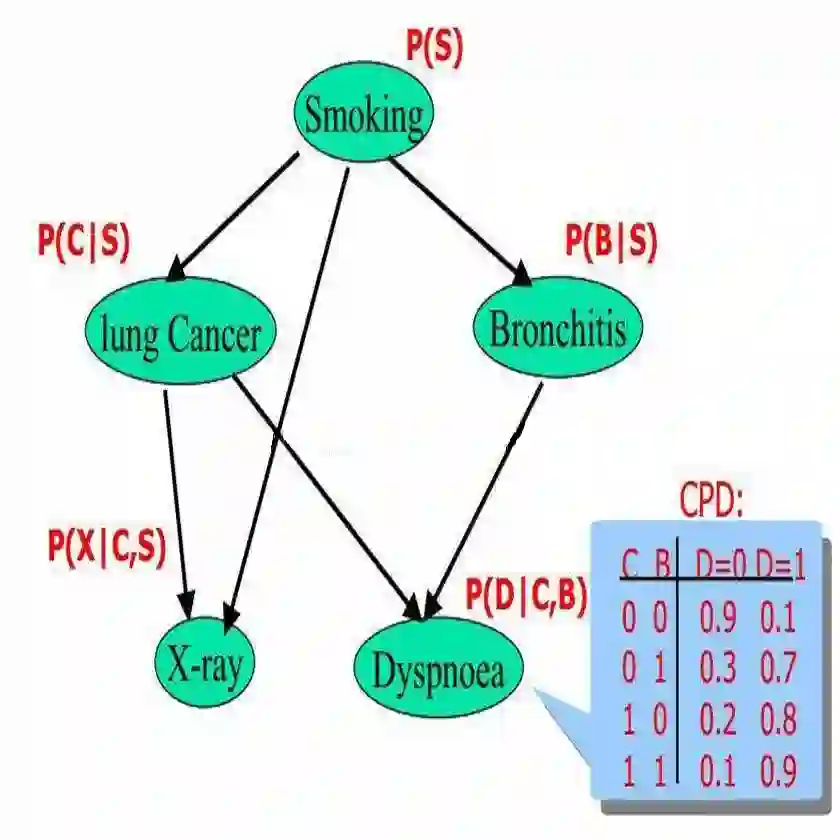
Inference is a fundamental reasoning technique in probability theory. When applied to a large joint distribution, it involves updating with evidence (conditioning) in one or more components (variables) and computing the outcome in other components. When the joint distribution is represented by a Bayesian network, the network structure may be exploited to proceed in a compositional manner -- with great benefits. However, the main challenge is that updating involves (re)normalisation, making it an operation that interacts badly with other operations. String diagrams are becoming popular as a graphical technique for probabilistic (and quantum) reasoning. Conditioning has appeared in string diagrams, in terms of a disintegration, using bent wires and shaded (or dashed) normalisation boxes. It has become clear that such normalisation boxes do satisfy certain compositional rules. This paper takes a decisive step in this development by adding a removal rule to the formalism, for the deletion of shaded boxes. Via this removal rule one can get rid of shaded boxes and terminate an inference argument. This paper illustrates via many (graphical) examples how the resulting compositional inference technique can be used for Bayesian networks, causal reasoning and counterfactuals.

翻译：推理是概率论中的一种基本推理技术。当应用于大型联合分布时，它涉及在一个或多个分量（变量）中根据证据进行更新（条件化），并计算其他分量的结果。当联合分布由贝叶斯网络表示时，可以利用网络结构以组合方式进行推理——这带来了巨大的优势。然而，主要挑战在于更新涉及（重新）归一化，使其成为一种与其他操作交互不佳的运算。弦图作为一种概率（及量子）推理的图形技术正日益流行。条件化已以瓦解的形式出现在弦图中，使用弯曲的线和带阴影（或虚线）的归一化框。现已明确，此类归一化框确实满足某些组合规则。本文在这一发展中迈出了决定性的一步，即在形式体系中增加了一条移除规则，用于删除带阴影的框。通过该移除规则，可以消除带阴影的框并终止推理论证。本文通过大量（图形化）示例说明了所得的组合推理技术如何用于贝叶斯网络、因果推理及反事实分析。