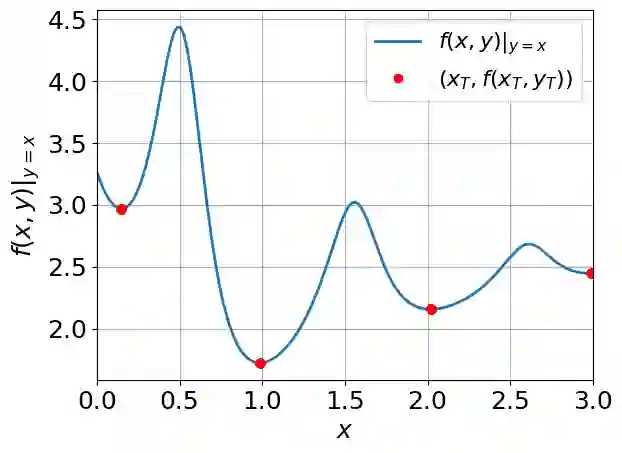
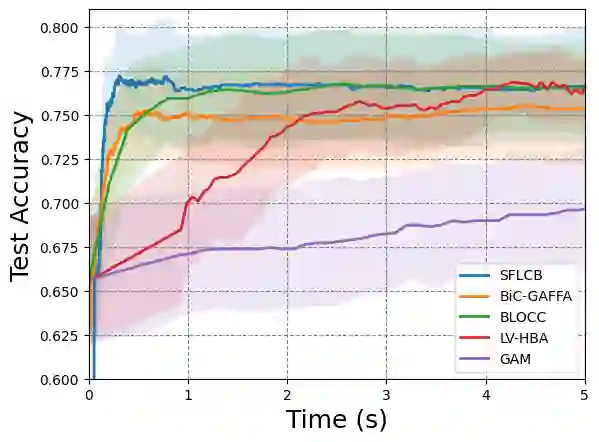
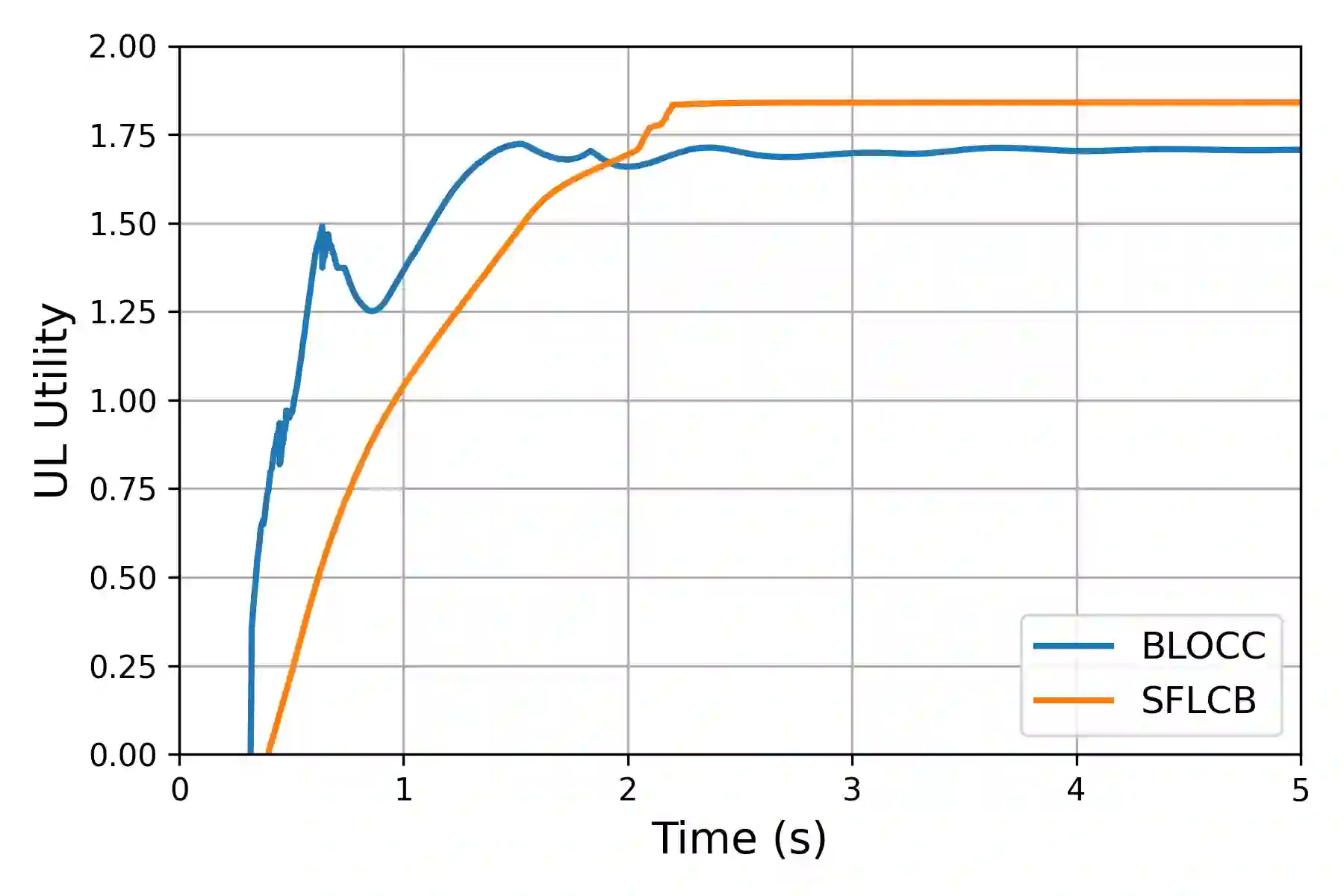
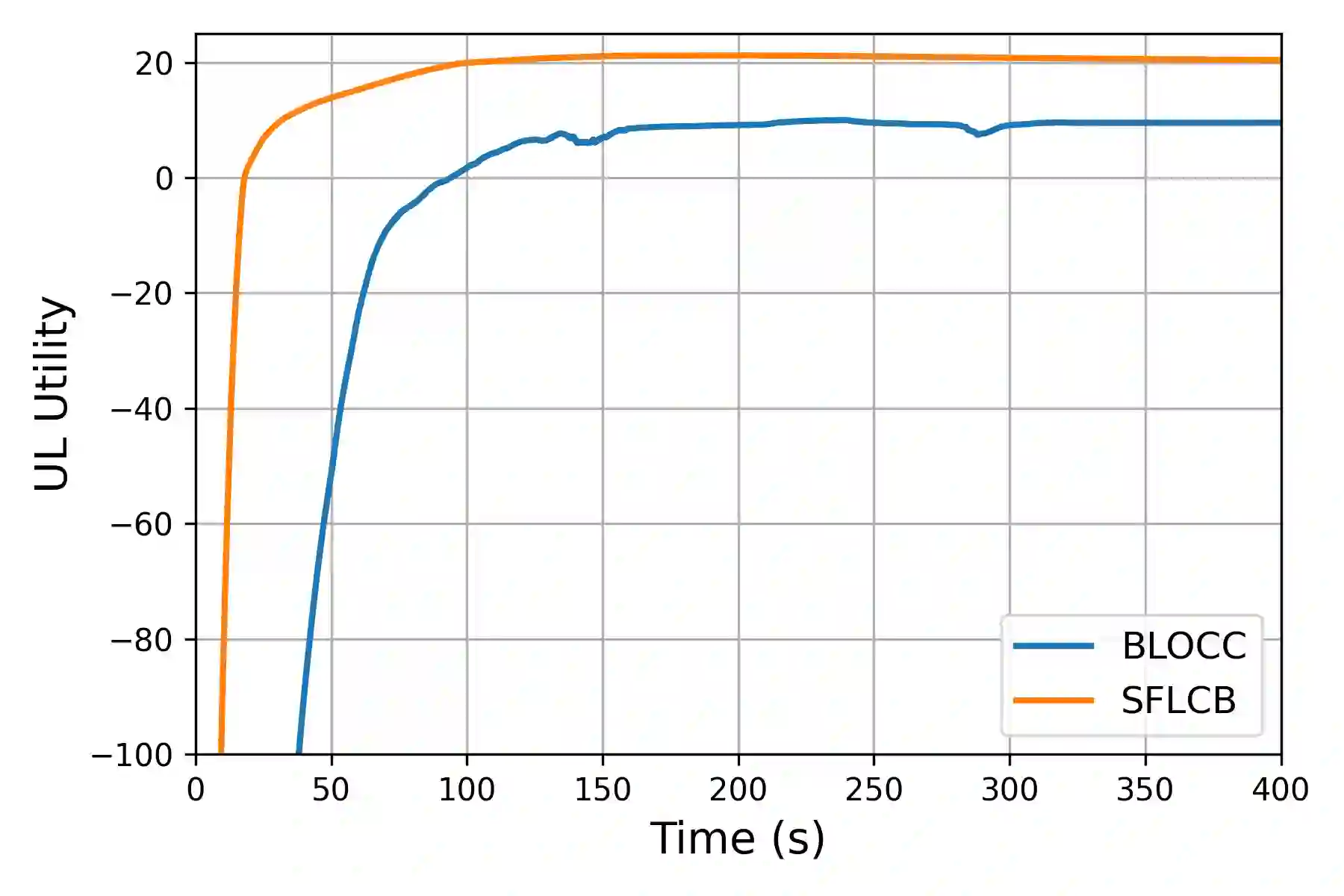
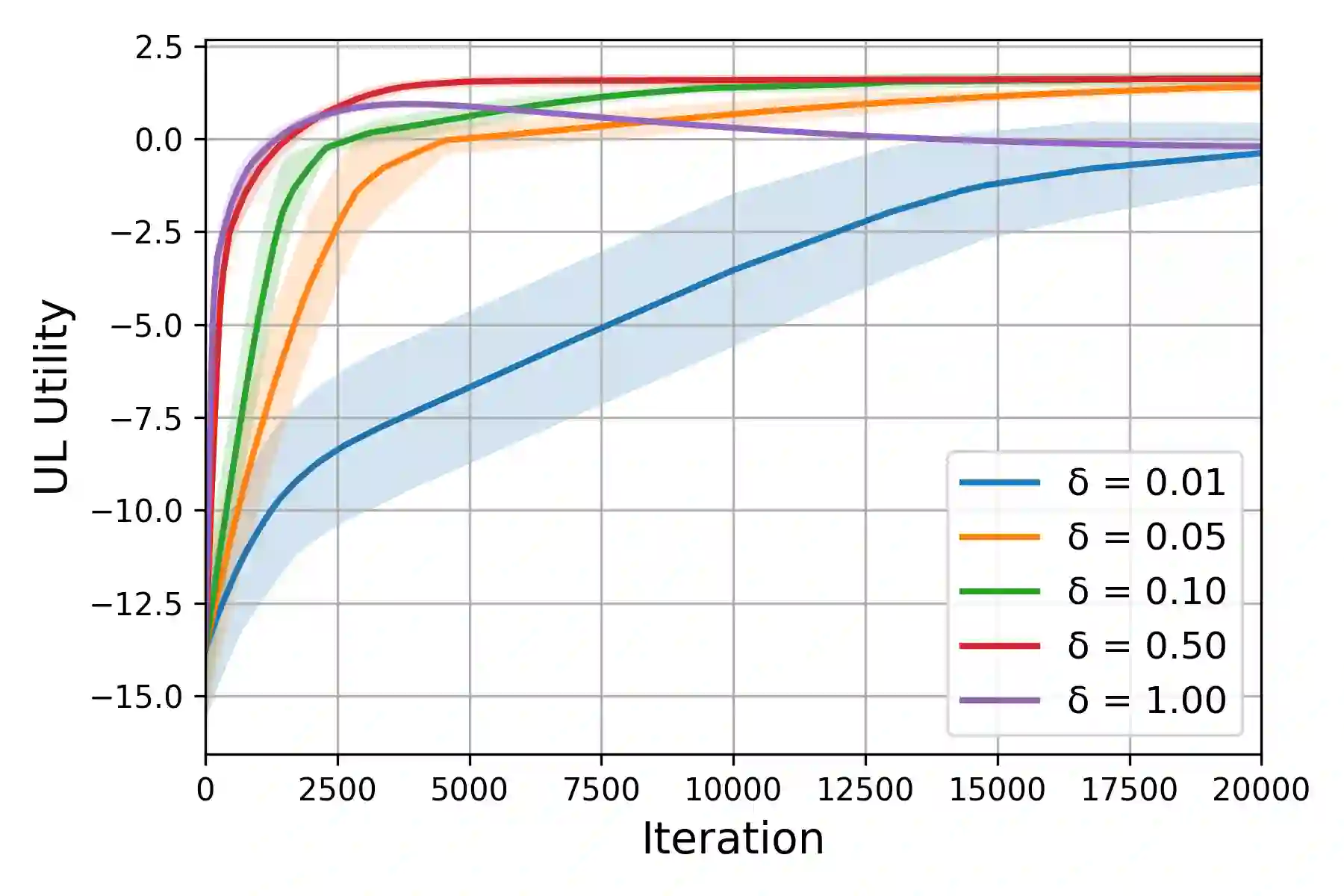
We study bilevel optimization problems where the lower-level problems are strongly convex and have coupled linear constraints. To overcome the potential non-smoothness of the hyper-objective and the computational challenges associated with the Hessian matrix, we utilize penalty and augmented Lagrangian methods to reformulate the original problem as a single-level one. Especially, we establish a strong theoretical connection between the reformulated function and the original hyper-objective by characterizing the closeness of their values and derivatives. Based on this reformulation, we propose a single-loop, first-order algorithm for linearly constrained bilevel optimization (SFLCB). We provide rigorous analyses of its non-asymptotic convergence rates, showing an improvement over prior double-loop algorithms -- form $O(\epsilon^{-3}\log(\epsilon^{-1}))$ to $O(\epsilon^{-3})$. The experiments corroborate our theoretical findings and demonstrate the practical efficiency of the proposed SFLCB algorithm. Simulation code is provided at https://github.com/ShenGroup/SFLCB.

翻译：本文研究一类下层问题为强凸且具有耦合线性约束的双层优化问题。为克服超目标函数可能的非光滑性及海森矩阵相关的计算难题，我们采用罚函数法与增广拉格朗日方法将原问题重构为单层优化问题。特别地，通过刻画重构函数与原始超目标函数在函数值及导数层面的逼近程度，我们建立了二者间的强理论关联。基于此重构框架，我们提出了一种用于线性约束双层优化的单循环一阶算法（SFLCB）。我们对其非渐近收敛速率进行了严格分析，证明其收敛阶从现有双循环算法的$O(\\epsilon^{-3}\\log(\\epsilon^{-1}))$提升至$O(\\epsilon^{-3})$。实验验证了理论结论，并证明了所提SFLCB算法的实际效率。仿真代码发布于 https://github.com/ShenGroup/SFLCB。