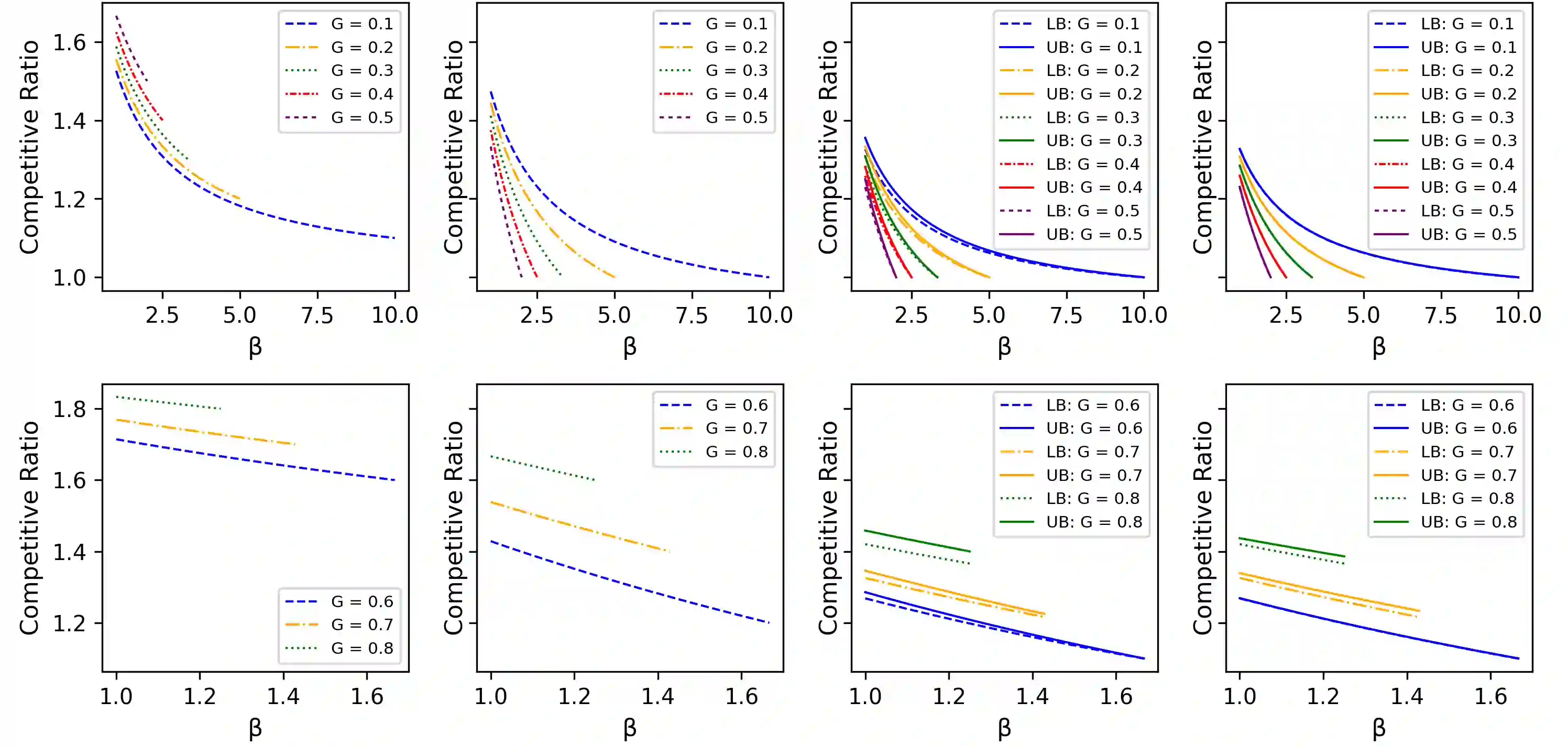
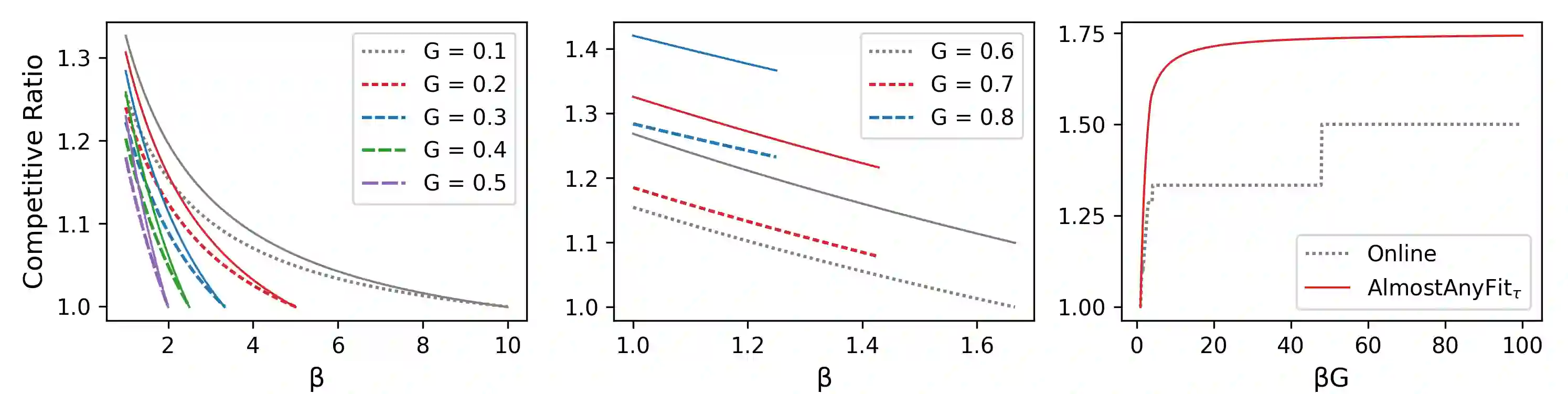
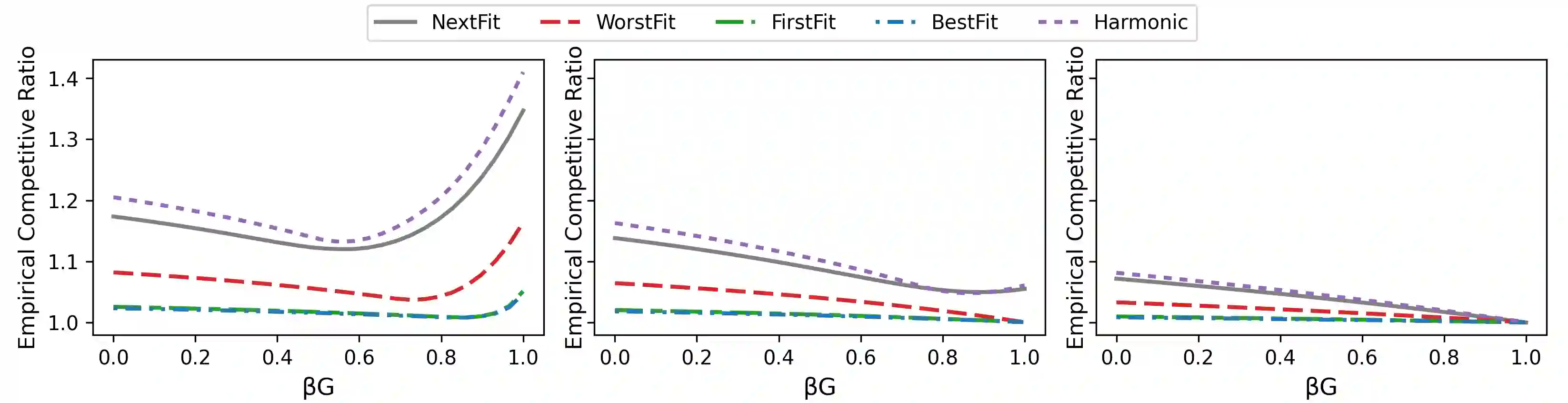
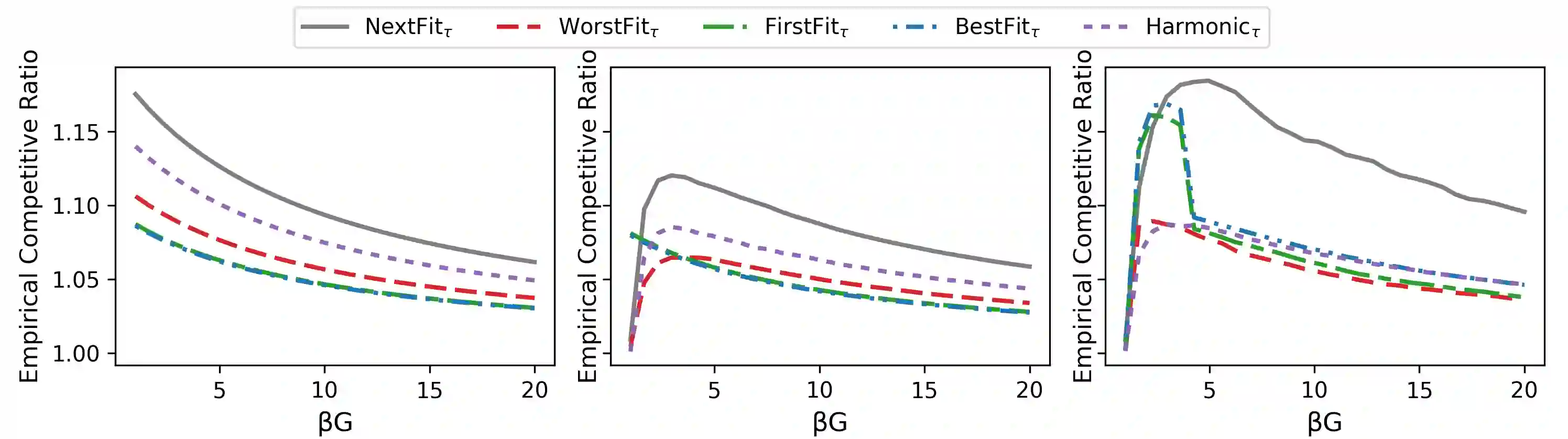
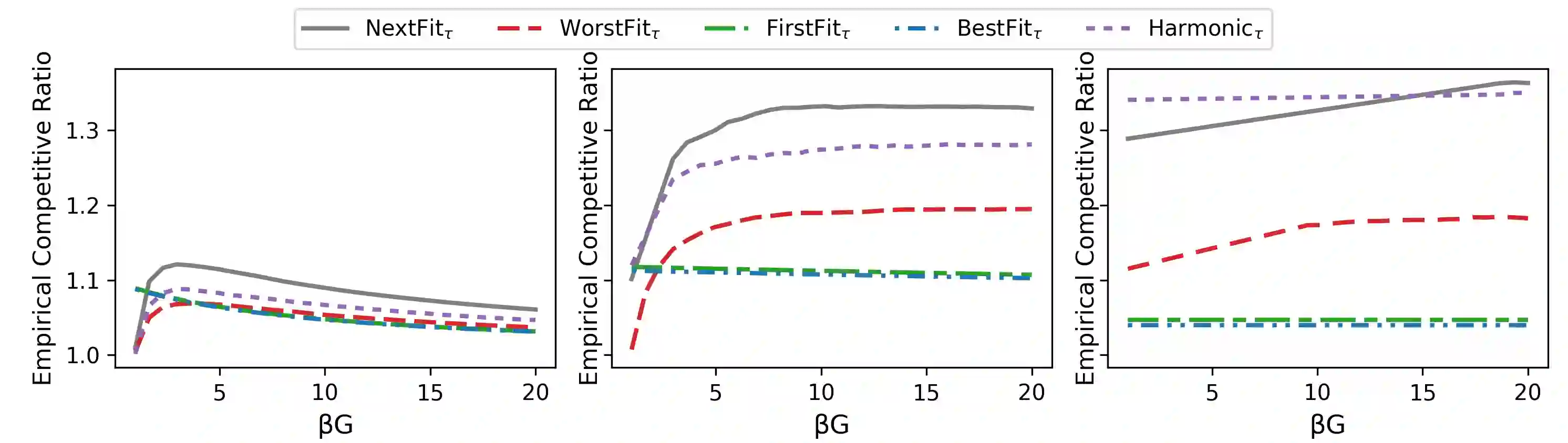
The online bin packing problem and its variants are regularly used to model server allocation problems. Modern concerns surrounding sustainability and overcommitment in cloud computing motivate bin packing models that capture costs associated with highly utilized servers. In this work, we introduce the green bin packing problem, an online variant with a linear cost $\beta$ for filling above a fixed level $G$. For a given instance, the goal is to minimize the sum of the number of opened bins and the linear cost. We show that when $\beta G \le 1$, classical online bin packing algorithms such as FirstFit or Harmonic perform well, and can achieve competitive ratios lower than in the classic setting. However, when $\beta G > 1$, new algorithmic solutions can improve both worst-case and typical performance. We introduce variants of classic online bin packing algorithms and establish theoretical bounds, as well as test their empirical performance.

翻译：在线装箱问题及其变体常被用于建模服务器资源分配问题。现代云计算中关于可持续性和资源过度分配的考量，催生了能够捕捉高利用率服务器相关成本的装箱模型。本研究提出了绿色装箱问题，这是一种在线变体，其特点是对超过固定阈值G的填充量施加线性成本β。对于给定实例，目标是最小化已开启箱体数量与线性成本之和。我们证明当βG ≤ 1时，经典在线装箱算法（如FirstFit或Harmonic）表现良好，其竞争比可低于经典设定下的结果。然而当βG > 1时，新的算法解决方案能够同时改善最坏情况与典型性能。我们提出了经典在线装箱算法的改进变体，建立了理论性能界限，并对其进行了实证性能测试。