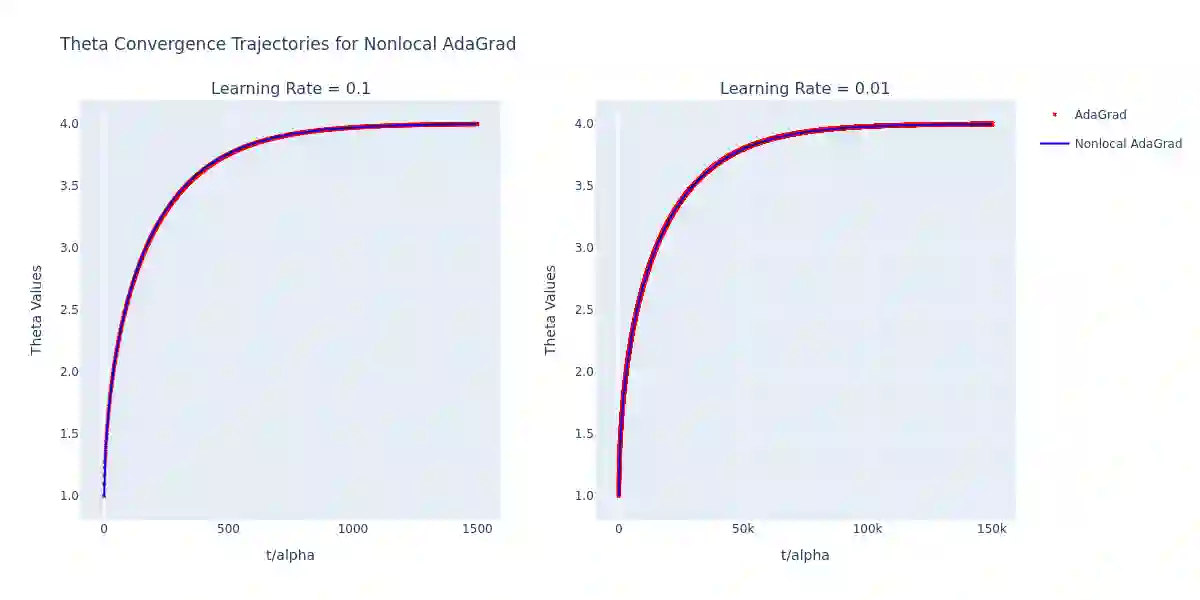
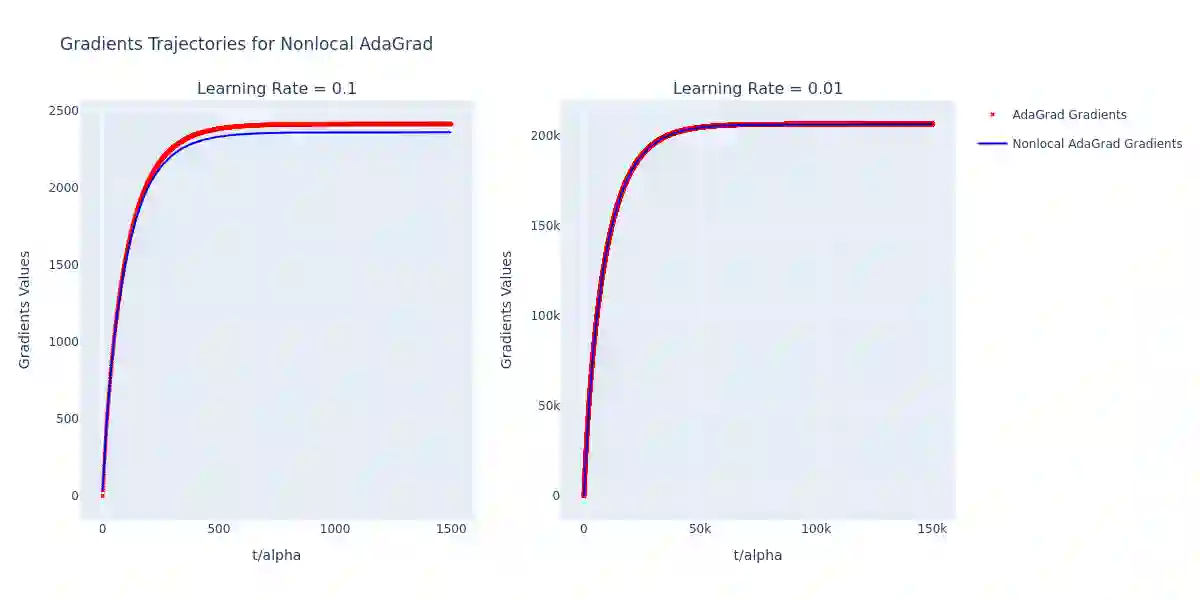
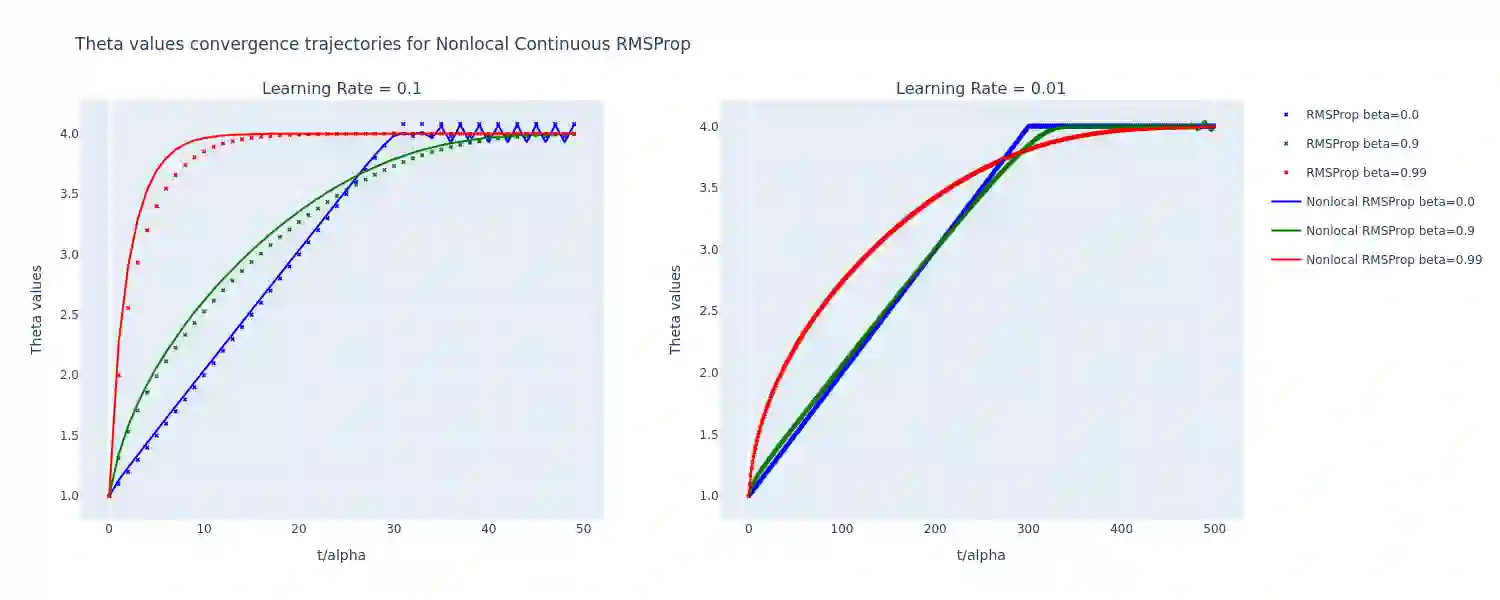
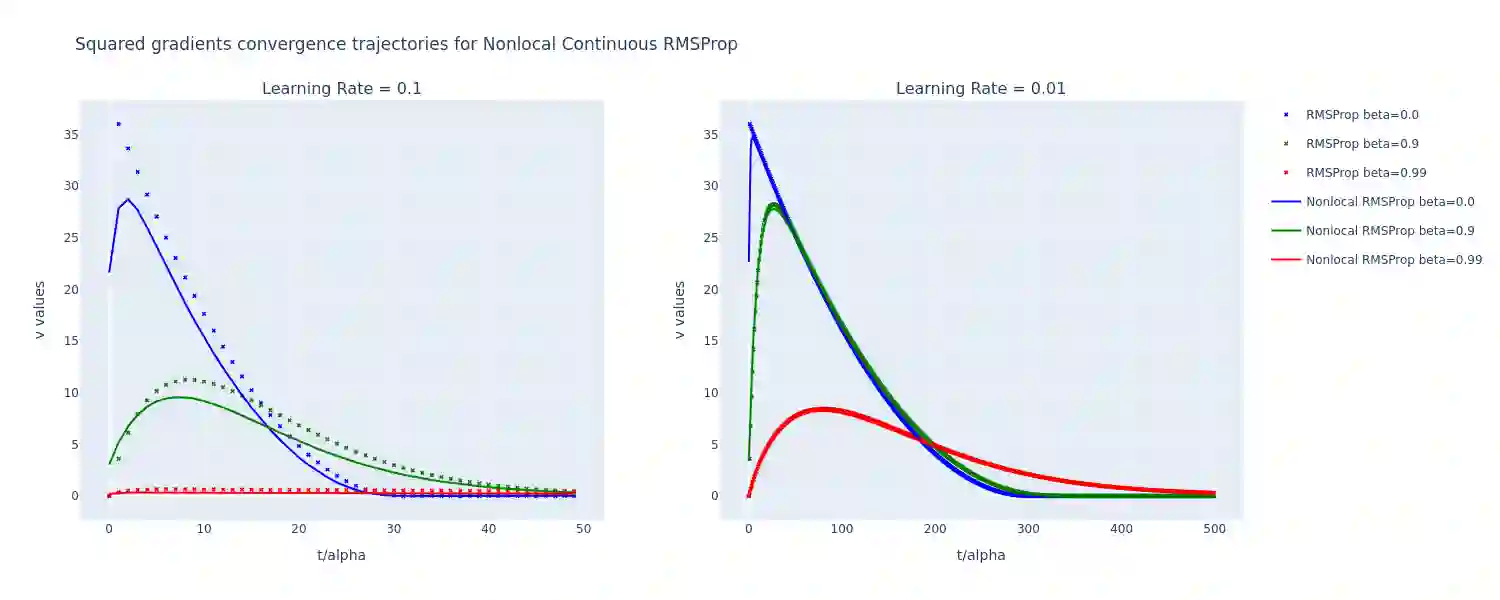
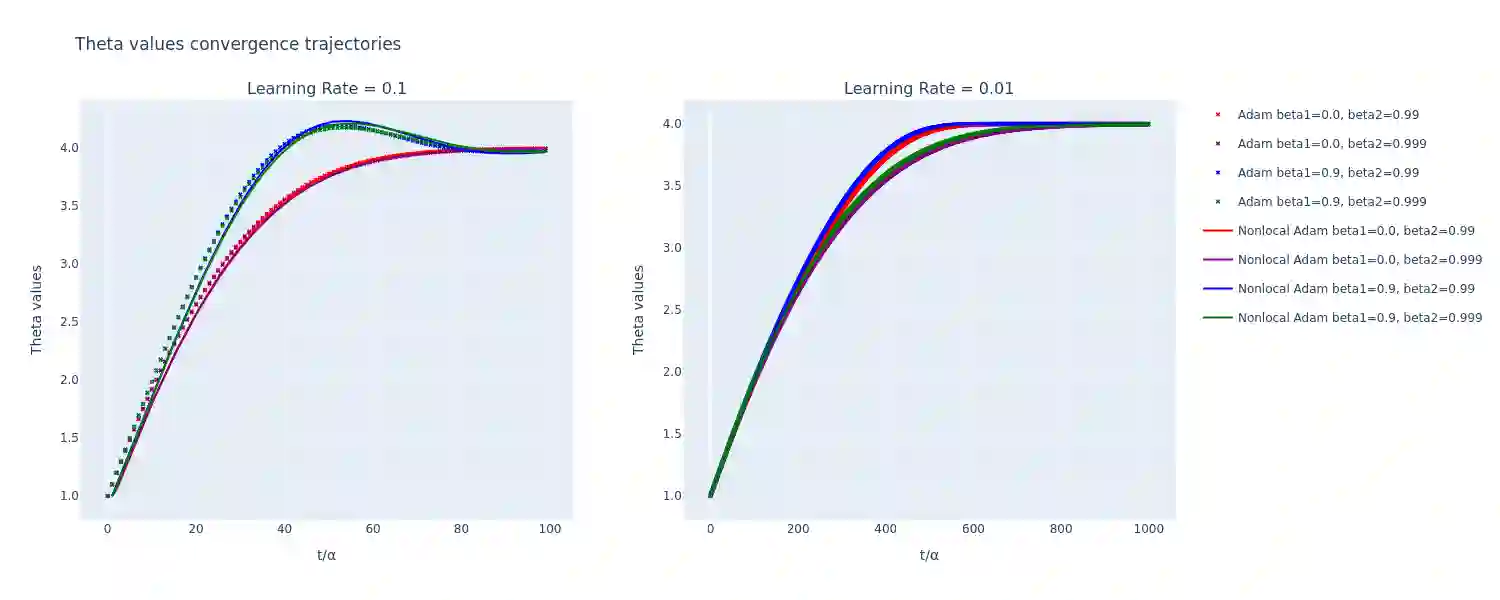
In this paper, we propose a continuous-time formulation for the AdaGrad, RMSProp, and Adam optimization algorithms by modeling them as first-order integro-differential equations. We perform numerical simulations of these equations, along with stability and convergence analyses, to demonstrate their validity as accurate approximations of the original algorithms. Our results indicate a strong agreement between the behavior of the continuous-time models and the discrete implementations, thus providing a new perspective on the theoretical understanding of adaptive optimization methods.

翻译：本文通过将AdaGrad、RMSProp与Adam优化算法建模为一阶积分-微分方程，提出了这些算法的连续时间表述。我们通过对这些方程进行数值模拟，并结合稳定性与收敛性分析，证明了其作为原始算法精确近似的有效性。研究结果表明，连续时间模型的行为与离散实现之间具有高度一致性，从而为理解自适应优化方法的理论机制提供了新的视角。