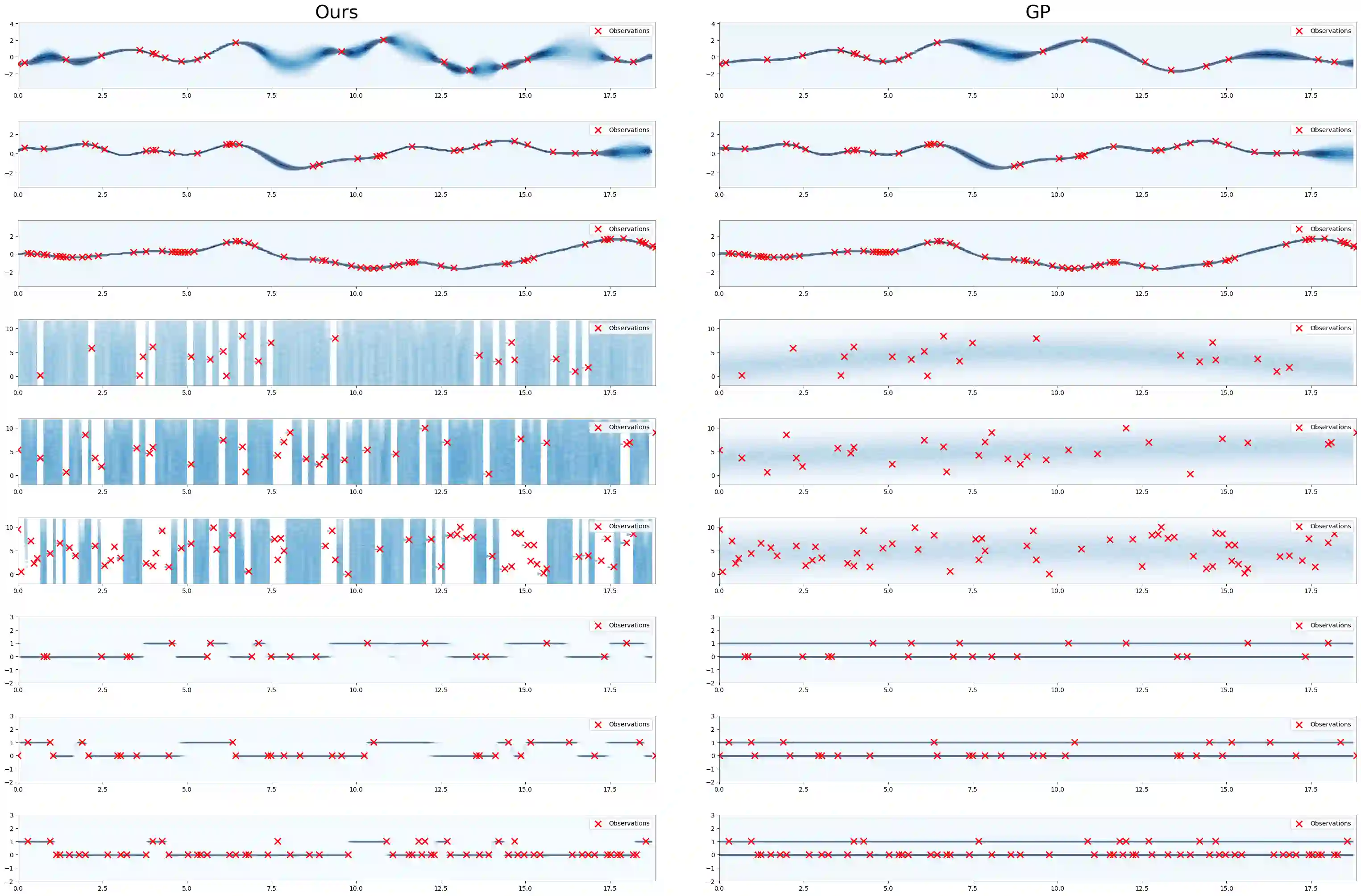
In this paper, a Convolution-Based Converter (CBC) is proposed to develop a methodology for removing the strong or fixed priors in estimating the probability distribution of targets based on observations in the stochastic process. Traditional approaches, e.g., Markov-based and Gaussian process-based methods, typically leverage observations to estimate targets based on strong or fixed priors (such as Markov properties or Gaussian prior). However, the effectiveness of these methods depends on how well their prior assumptions align with the characteristics of the problem. When the assumed priors are not satisfied, these approaches may perform poorly or even become unusable. To overcome the above limitation, we introduce the Convolution-Based converter (CBC), which implicitly estimates the conditional probability distribution of targets without strong or fixed priors, and directly outputs the expected trajectory of the stochastic process that satisfies the constraints from observations. This approach reduces the dependence on priors, enhancing flexibility and adaptability in modeling stochastic processes when addressing different problems. Experimental results demonstrate that our method outperforms existing baselines across multiple metrics.

翻译：本文提出了一种基于卷积的转换器（CBC），旨在建立一种方法论，用于消除在随机过程中基于观测值估计目标概率分布时所依赖的强先验或固定先验。传统方法（例如基于马尔可夫和基于高斯过程的方法）通常利用观测值，基于强先验或固定先验（如马尔可夫性质或高斯先验）来估计目标。然而，这些方法的有效性取决于其先验假设与问题特性的匹配程度。当假设的先验条件不满足时，这些方法可能表现不佳甚至无法使用。为克服上述局限，我们引入了基于卷积的转换器（CBC），它能够在没有强先验或固定先验的情况下隐式估计目标的条件概率分布，并直接输出满足观测约束的随机过程的期望轨迹。该方法降低了对先验的依赖，从而在处理不同问题时增强了随机过程建模的灵活性与适应性。实验结果表明，我们的方法在多项指标上均优于现有基线。