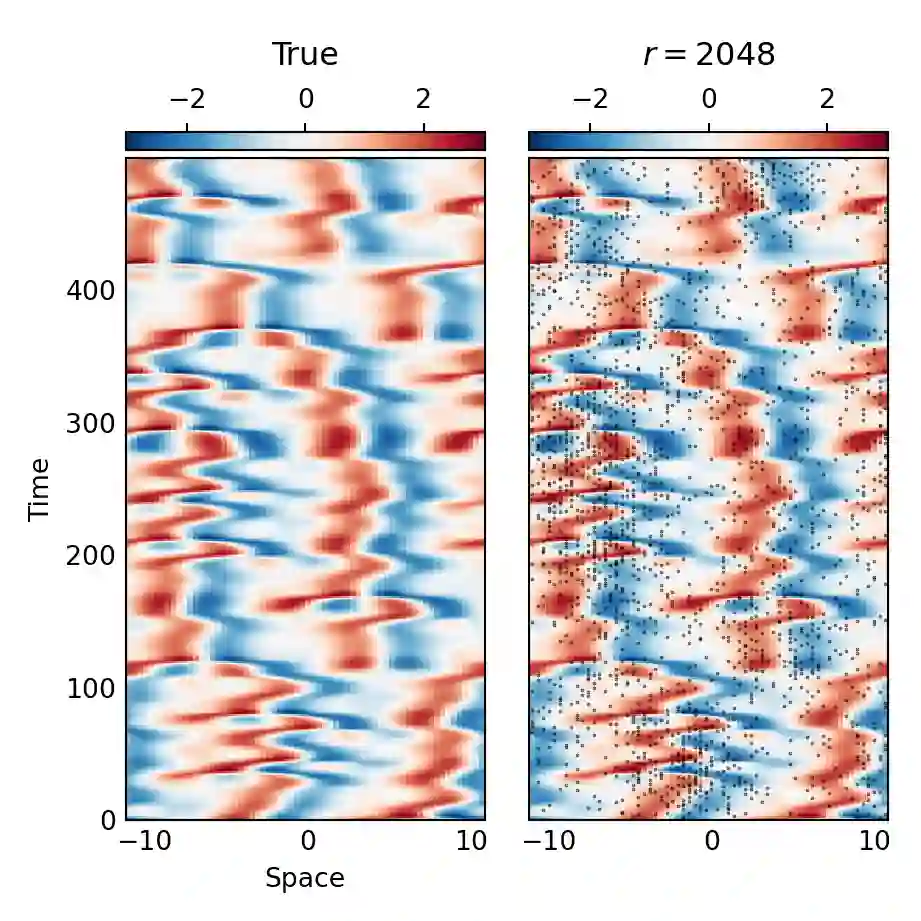
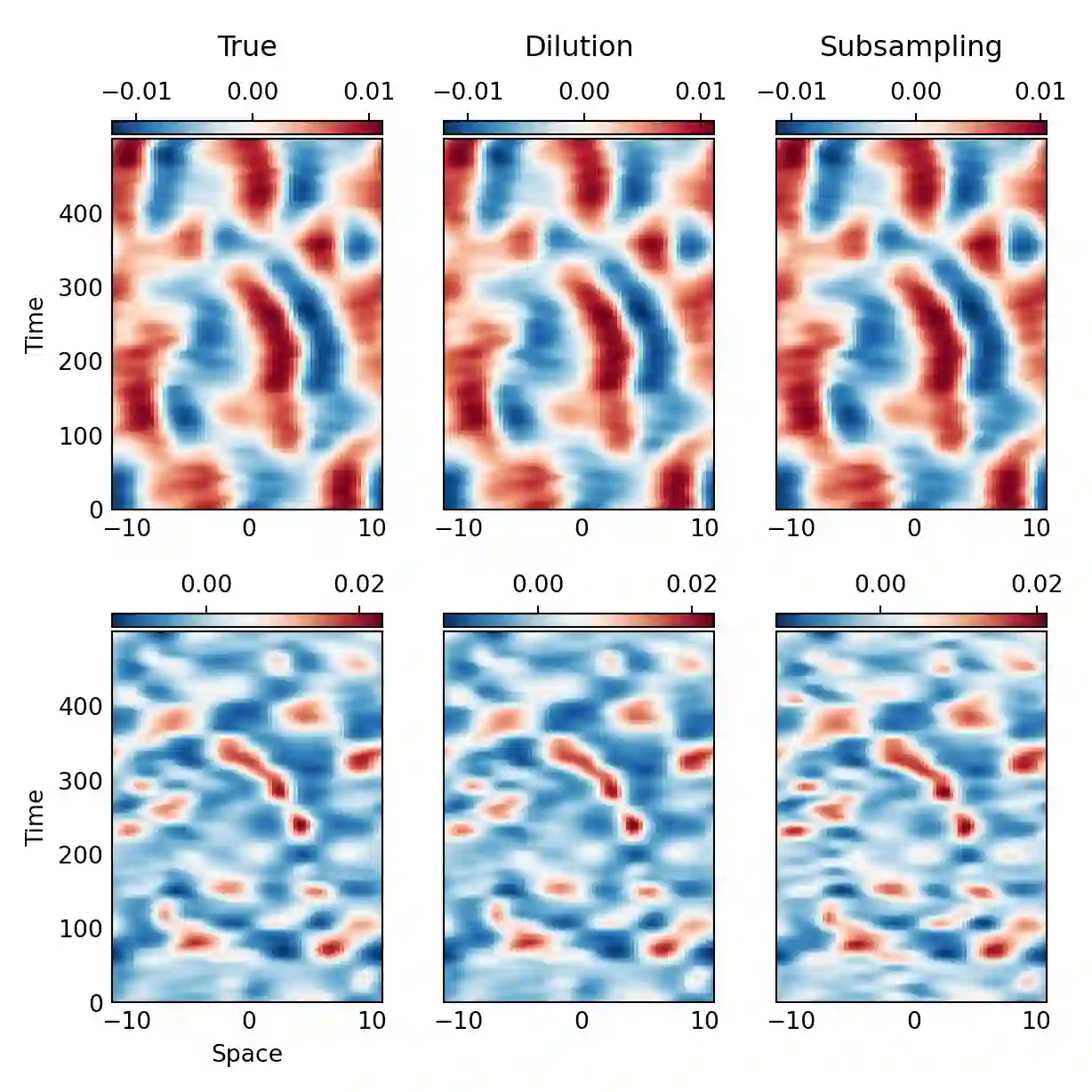
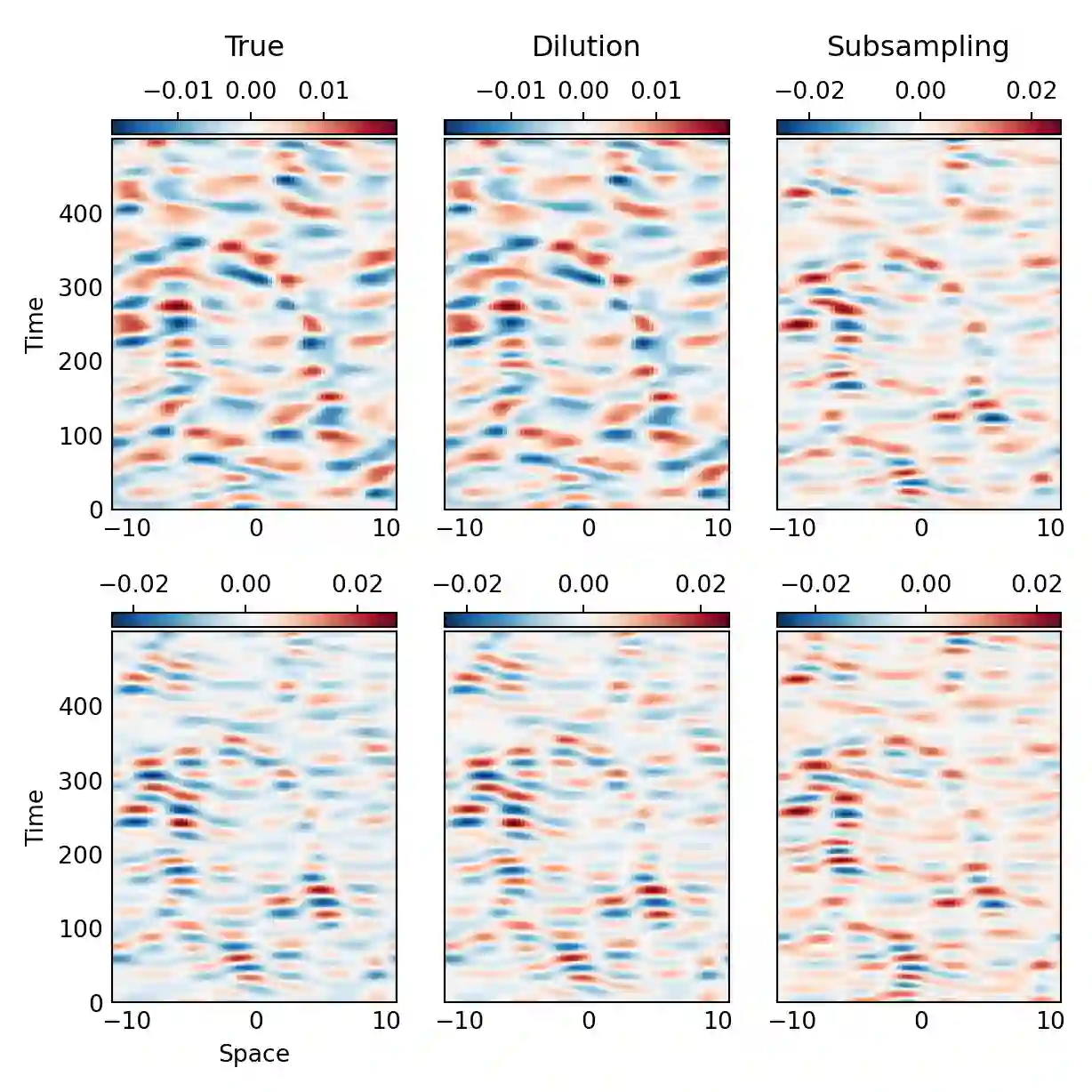
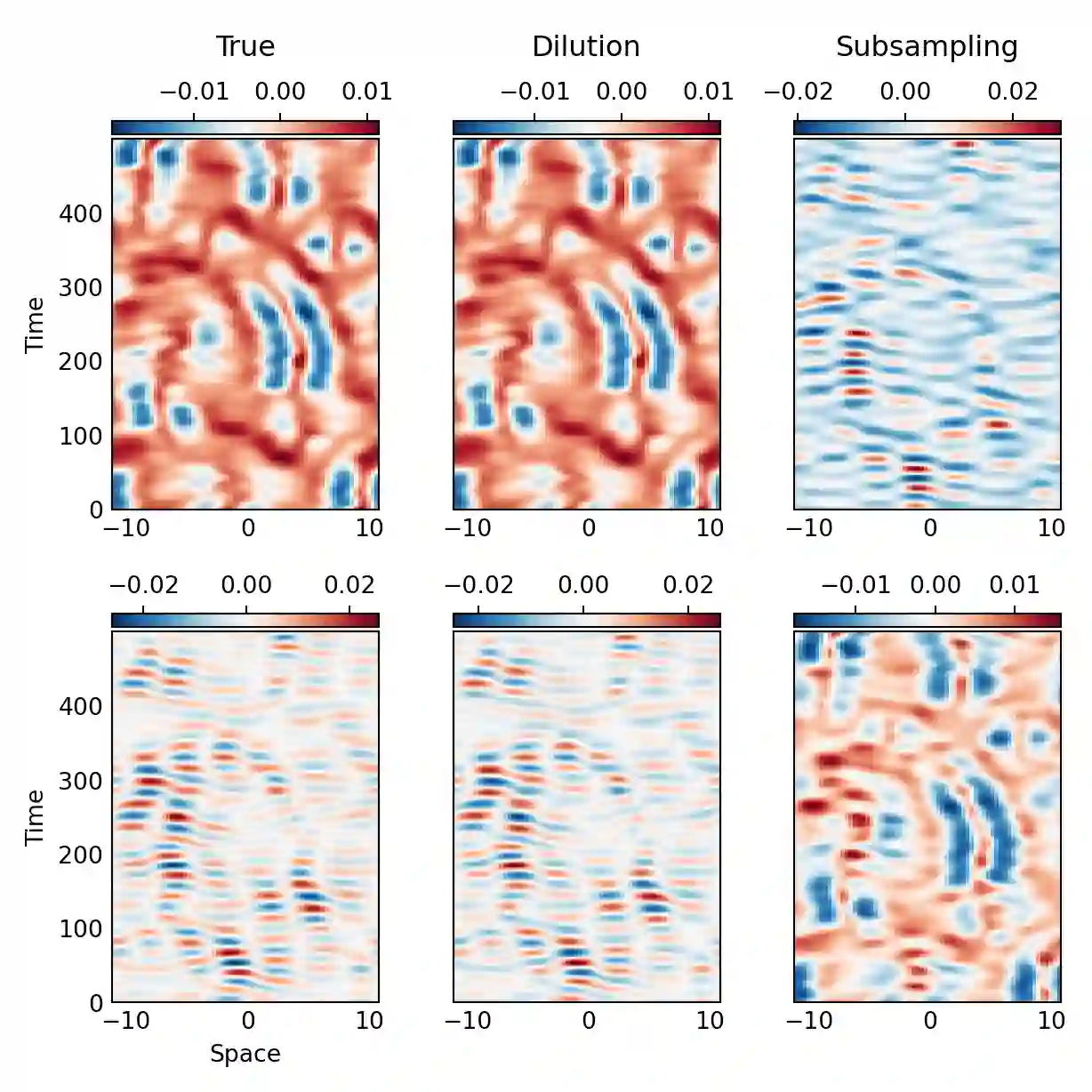
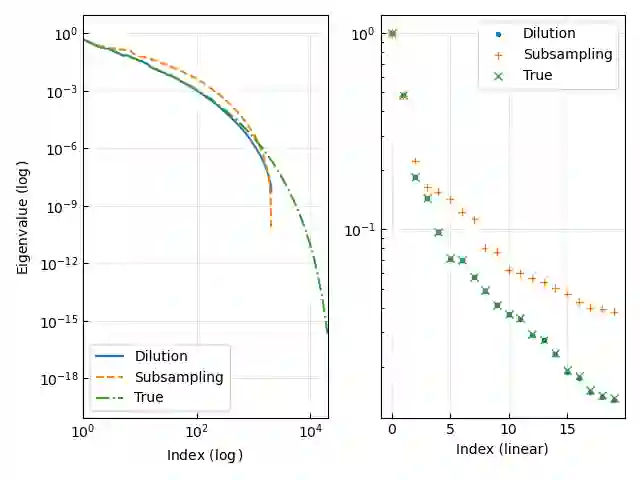
We develop an accelerated algorithm for computing an approximate eigenvalue decomposition of bistochastic normalized kernel matrices. Our approach constructs a low rank approximation of the original kernel matrix by the pivoted partial Cholesky algorithm and uses it to compute an approximate decomposition of its bistochastic normalization without requiring the formation of the full kernel matrix. The cost of the proposed algorithm depends linearly on the size of the employed training dataset and quadratically on the rank of the low rank approximation, offering a significant cost reduction compared to the naive approach. We apply the proposed algorithm to the kernel based extraction of spatiotemporal patterns from chaotic dynamics, demonstrating its accuracy while also comparing it with an alternative algorithm consisting of subsampling and Nystroem extension.

翻译：本文提出一种加速算法，用于计算双随机归一化核矩阵的近似特征值分解。该方法通过枢轴部分Cholesky算法构建原始核矩阵的低秩近似，并利用该近似计算其双随机归一化矩阵的近似分解，而无需构建完整的核矩阵。所提算法的计算成本与训练数据集规模呈线性关系，与低秩近似的秩呈二次关系，相比传统方法显著降低了计算开销。我们将该算法应用于基于核方法的混沌动力学时空模式提取，验证了其准确性，并与基于子采样和Nyström扩展的替代算法进行了对比分析。