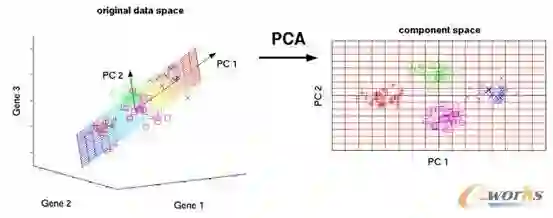
We introduce Principal Component Analysis guided Quantile Sampling (PCA QS), a novel sampling framework designed to preserve both the statistical and geometric structure of large scale datasets. Unlike conventional PCA, which reduces dimensionality at the cost of interpretability, PCA QS retains the original feature space while using leading principal components solely to guide a quantile based stratification scheme. This principled design ensures that sampling remains representative without distorting the underlying data semantics. We establish rigorous theoretical guarantees, deriving convergence rates for empirical quantiles, Kullback Leibler divergence, and Wasserstein distance, thus quantifying the distributional fidelity of PCA QS samples. Practical guidelines for selecting the number of principal components, quantile bins, and sampling rates are provided based on these results. Extensive empirical studies on both synthetic and real-world datasets show that PCA QS consistently outperforms simple random sampling, yielding better structure preservation and improved downstream model performance. Together, these contributions position PCA QS as a scalable, interpretable, and theoretically grounded solution for efficient data summarization in modern machine learning workflows.

翻译：我们提出了一种主成分分析引导的分位数抽样（PCA QS）框架，这是一种新颖的抽样方法，旨在同时保持大规模数据集的统计与几何结构。与传统的PCA通过牺牲可解释性来降低维度不同，PCA QS保留了原始特征空间，仅利用前导主成分来指导基于分位数的分层方案。这种原则性设计确保了抽样具有代表性，同时不会扭曲底层数据的语义。我们建立了严格的理论保证，推导了经验分位数、Kullback-Leibler散度和Wasserstein距离的收敛速率，从而量化了PCA QS样本的分布保真度。基于这些结果，我们为选择主成分数量、分位数箱和抽样率提供了实用指南。在合成和真实数据集上的大量实证研究表明，PCA QS始终优于简单随机抽样，实现了更好的结构保持和更优的下游模型性能。这些贡献共同使PCA QS成为一种可扩展、可解释且理论依据充分的解决方案，适用于现代机器学习工作流中的高效数据摘要。