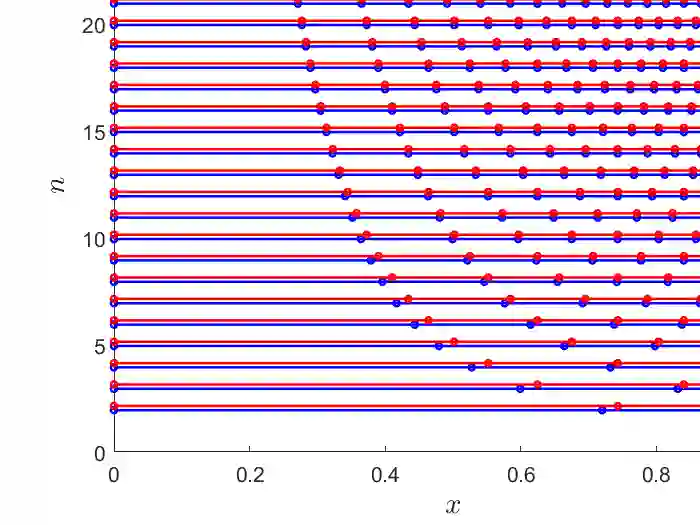
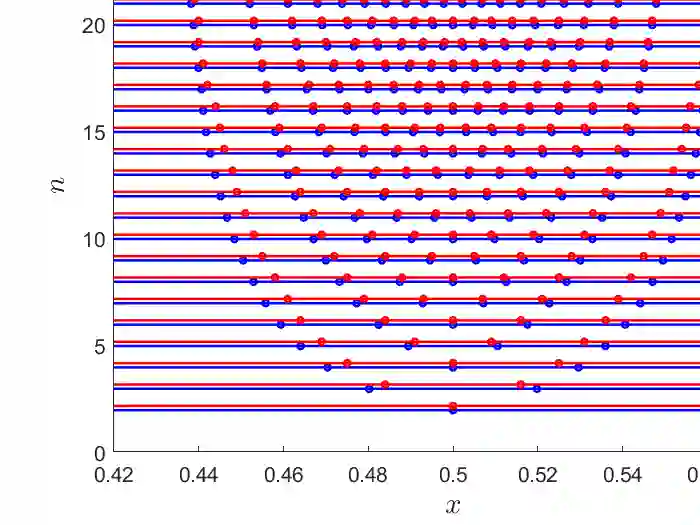
We consider the minimization of integral functionals in one dimension and their approximation by $r$-adaptive finite elements. Including the grid of the FEM approximation as a variable in the minimization, we are able to show that the optimal grid configurations have a well-defined limit when the number of nodes in the grid is being sent to infinity. This is done by showing that the suitably renormalized energy functionals possess a limit in the sense of $\Gamma$-convergence. We provide numerical examples showing the closeness of the optimal asymptotic mesh obtained as a minimizer of the $\Gamma$-limit to the optimal finite meshes.

翻译：我们考虑一维积分泛函的最小化问题及其通过$r$-自适应有限元的近似方法。将有限元近似中的网格作为最小化问题中的变量，我们能够证明当网格节点数趋于无穷时，最优网格配置具有明确定义的极限。这是通过证明适当重归一化的能量泛函在$\Gamma$-收敛意义下存在极限来实现的。我们提供了数值示例，展示了作为$\Gamma$-极限最小化子得到的最优渐近网格与最优有限网格的接近程度。