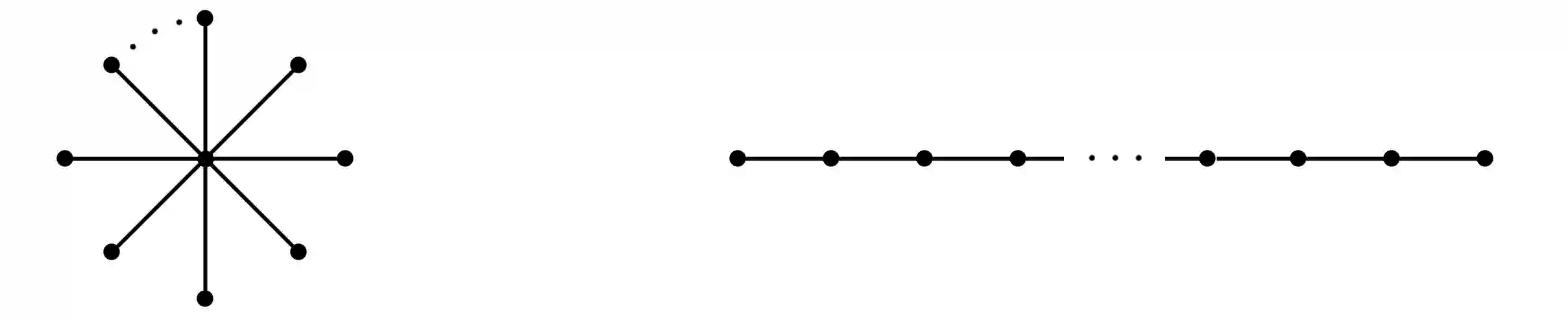
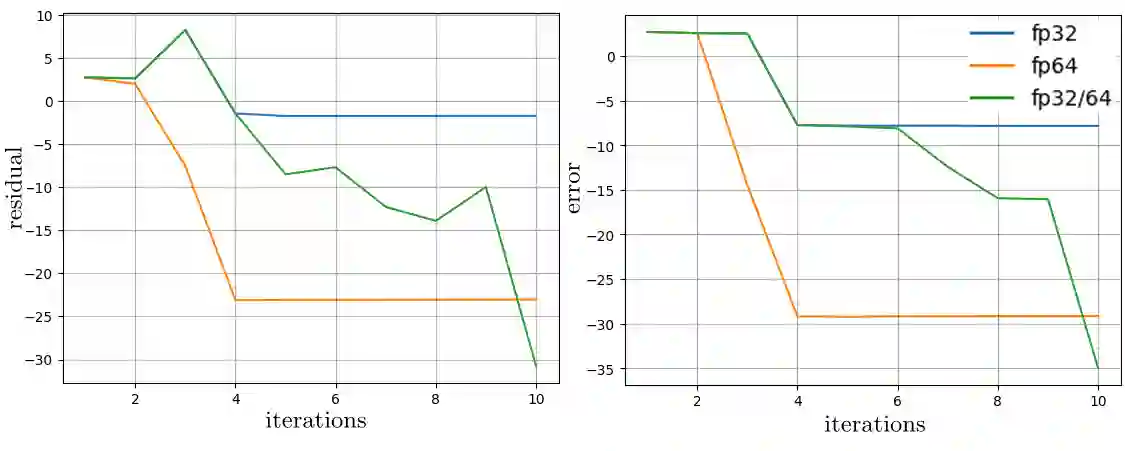
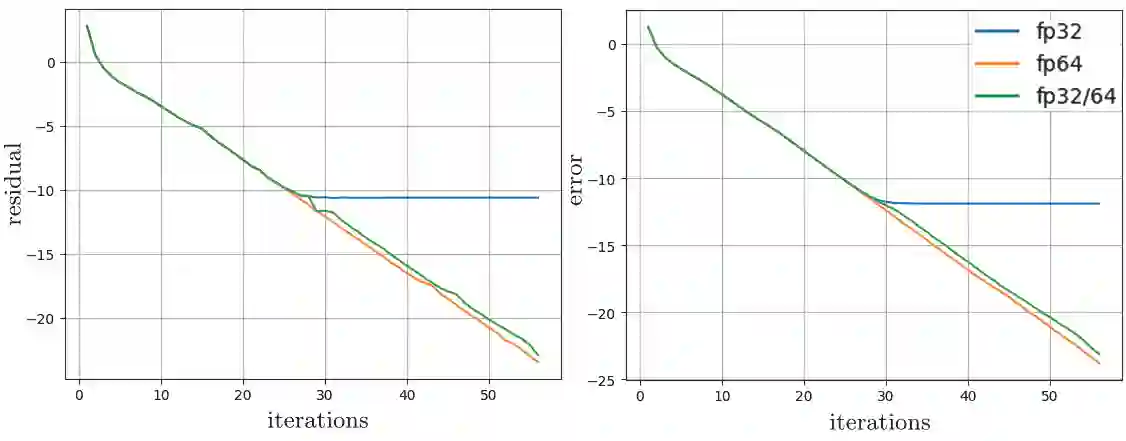
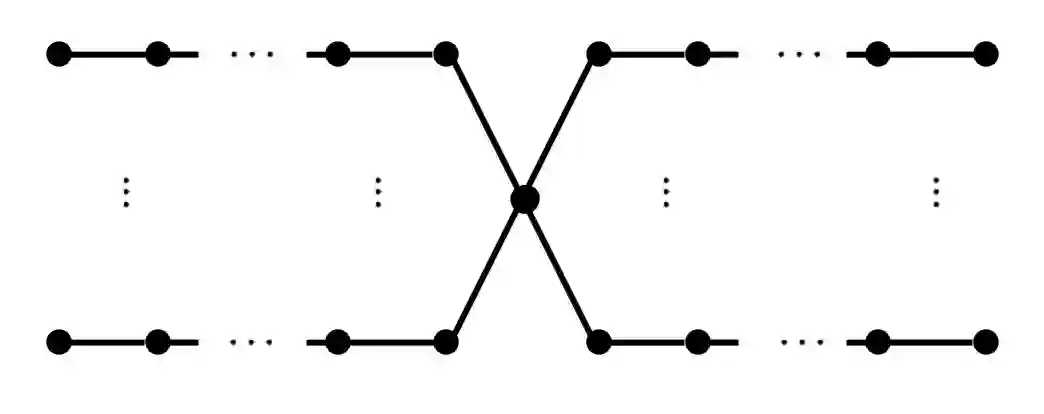
The problem of optimal precision switching for the conjugate gradient (CG) method applied to sparse linear systems is considered. A sparse matrix is defined as an $n\!\times\!n$ matrix with $m\!=\!O(n)$ nonzero entries. The algorithm first computes an approximate solution in single precision with tolerance $\varepsilon_1$, then switches to double precision to refine the solution to the required stopping tolerance $\varepsilon_2$. Based on estimates of system matrix parameters -- computed in time which does not exceed $1\%$ of the time needed to solve the system in double precision -- we determine the optimal value of $\varepsilon_1$ that minimizes total computation time. This value is obtained by classifying the matrix using the $k$-nearest neighbors method on a small precomputed sample. Classification relies on a feature vector comprising: the matrix size $n$, the number of nonzeros $m$, the pseudo-diameter of the matrix sparsity graph, and the average rate of residual norm decay during the early CG iterations in single precision. We show that, in addition to the matrix condition number, the diameter of the sparsity graph influences the growth of rounding errors during iterative computations. The proposed algorithm reduces the computational complexity of the CG -- expressed in equivalent double-precision iterations -- by more than $17\%$ on average across the considered matrix types in a sequential setting. The resulting speedup is at most $1.5\%$ worse than that achieved with the optimal (oracle) choice of $\varepsilon_1$. While the impact of matrix structure on Krylov subspace method convergence is well understood, the use of the sparsity graph diameter as a predictive feature for rounding error growth in mixed-precision CG appears to be novel. To the best of our knowledge, no prior work employs graph diameter to guide precision switching in iterative linear solvers.

翻译：本文研究了应用于稀疏线性系统的共轭梯度（CG）方法的最优精度切换问题。稀疏矩阵定义为具有 $m\!=\!O(n)$ 个非零元素的 $n\!\times\!n$ 矩阵。该算法首先以容差 $\varepsilon_1$ 在单精度下计算近似解，然后切换至双精度以将解细化至所需的停止容差 $\varepsilon_2$。基于对系统矩阵参数的估计（其计算时间不超过在双精度下求解系统所需时间的 $1\%$），我们确定了能最小化总计算时间的 $\varepsilon_1$ 最优值。该值通过对矩阵在一个小型预计算样本上使用 $k$ 近邻方法进行分类而获得。分类依赖于一个包含以下分量的特征向量：矩阵规模 $n$、非零元数量 $m$、矩阵稀疏性图的伪直径，以及在单精度下早期 CG 迭代过程中残差范数衰减的平均速率。我们证明，除了矩阵条件数外，稀疏性图的直径也会影响迭代计算过程中舍入误差的增长。在顺序计算环境下，对所考虑的矩阵类型，所提算法将 CG 的计算复杂度（以等效的双精度迭代次数表示）平均降低了 $17\%$ 以上。由此获得的加速效果最多比使用最优（先知）$\varepsilon_1$ 选择所实现的加速效果低 $1.5\%$。虽然矩阵结构对 Krylov 子空间方法收敛性的影响已得到充分理解，但利用稀疏性图直径作为混合精度 CG 中舍入误差增长的预测特征似乎是新颖的。据我们所知，尚无先前工作利用图直径来指导迭代线性求解器中的精度切换。