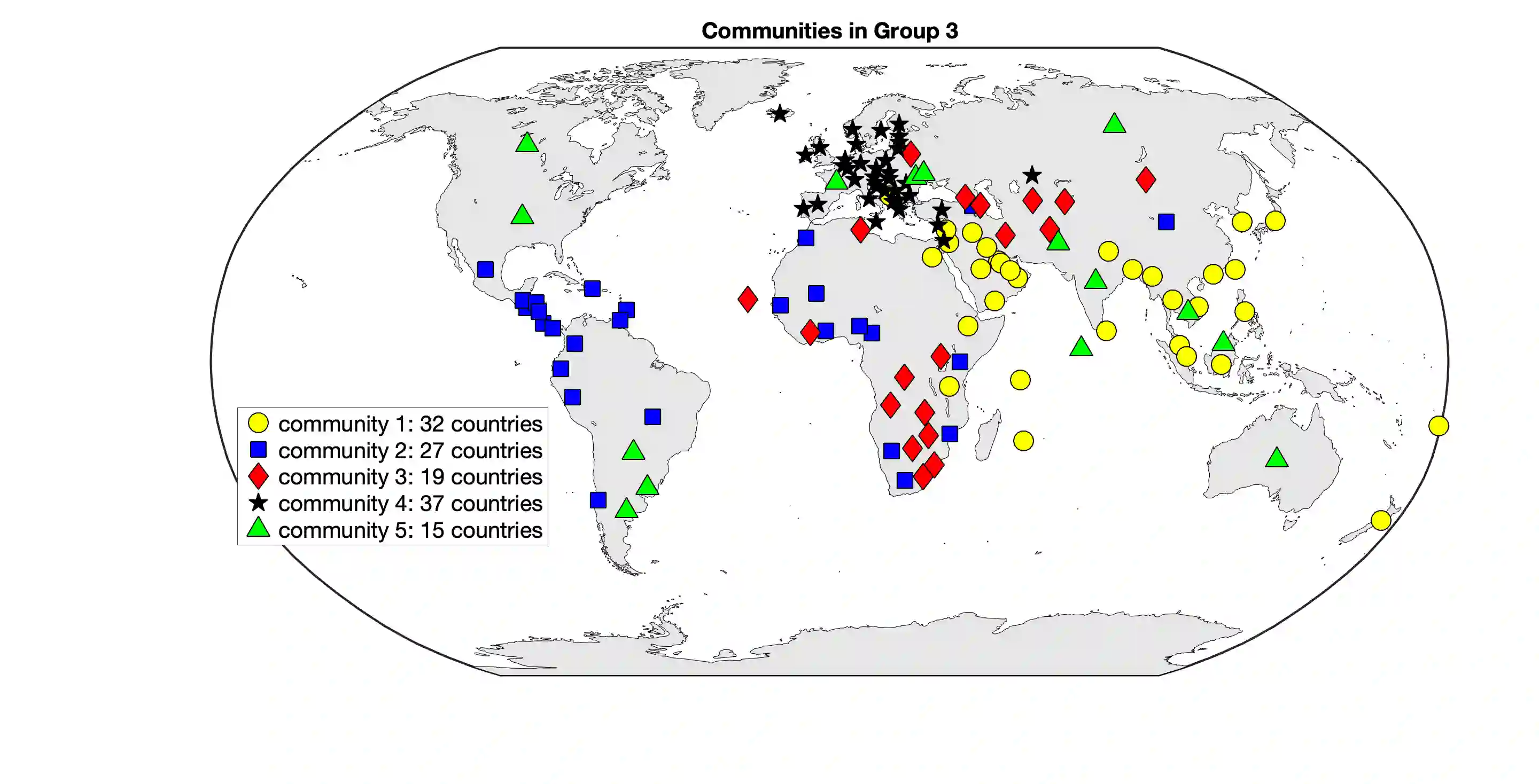
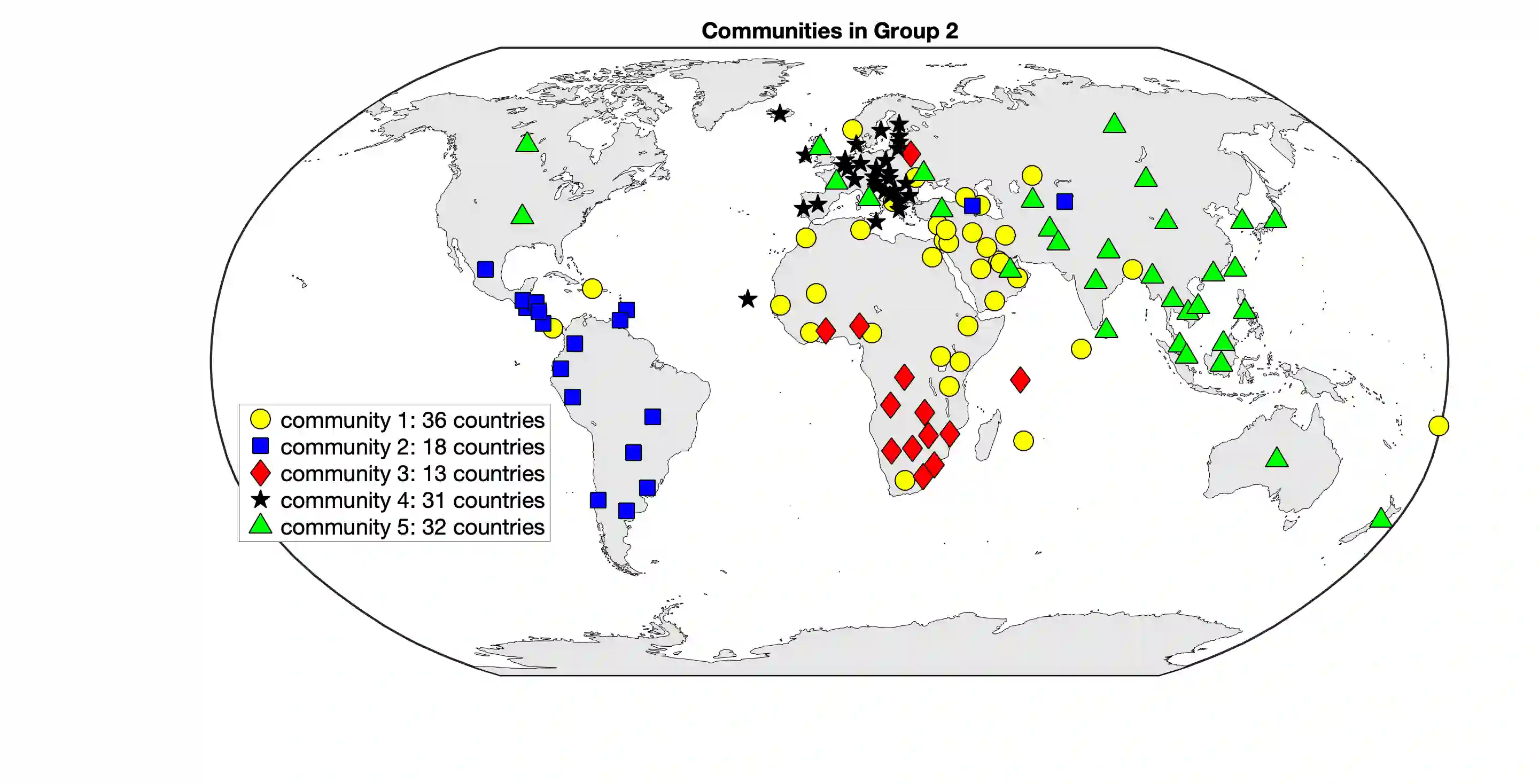
The paper considers the DIverse MultiPLEx (DIMPLE) network model, introduced in Pensky and Wang (2021), where all layers of the network have the same collection of nodes and are equipped with the Stochastic Block Models. In addition, all layers can be partitioned into groups with the same community structures, although the layers in the same group may have different matrices of block connection probabilities. The DIMPLE model generalizes a multitude of papers that study multilayer networks with the same community structures in all layers, as well as the Mixture Multilayer Stochastic Block Model (MMLSBM), where the layers in the same group have identical matrices of block connection probabilities. While Pensky and Wang (2021) applied spectral clustering to the proxy of the adjacency tensor, the present paper uses Sparse Subspace Clustering (SSC) for identifying groups of layers with identical community structures. Under mild conditions, the latter leads to the strongly consistent between-layer clustering. In addition, SSC allows to handle much larger networks than methodology of Pensky and Wang (2021), and is perfectly suitable for application of parallel computing.

翻译：文件考虑了Pensky和Wang(2021年)采用的DIverse 多元PLEX(DIMPLE)网络模型,该网络的所有层都有相同的节点集合,并配有“碎块模型”,此外,所有层可以分成具有相同的群落结构的组群,尽管同一组群的层可能具有不同的块状连接概率矩阵。DIMPLE模型概括了大量论文,这些论文研究多层网络和所有层群落结构相同的多层网络,以及混合多层群落模型(MMMLSBM),同一组群群的层群拥有相同的块状连接概率矩阵。Pensky和Wang(2021年)将光谱集群用于替代相邻区块群落结构,本文则使用偏差的子层群集(SSC)来识别具有相同群落结构的层群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群落群