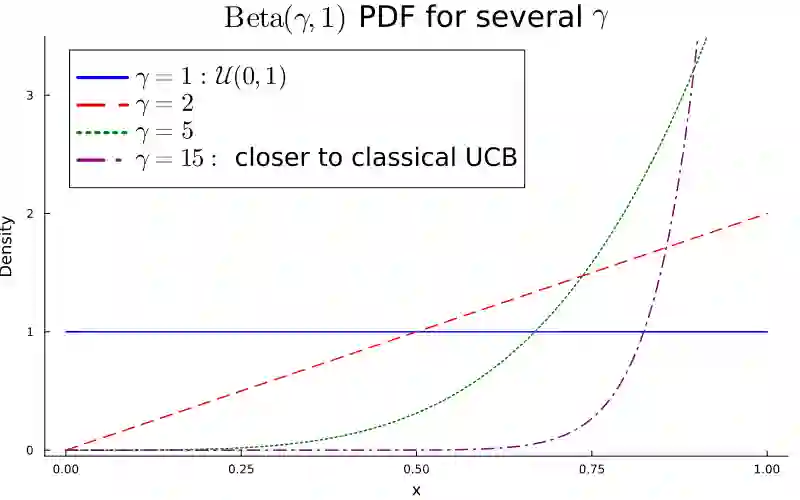
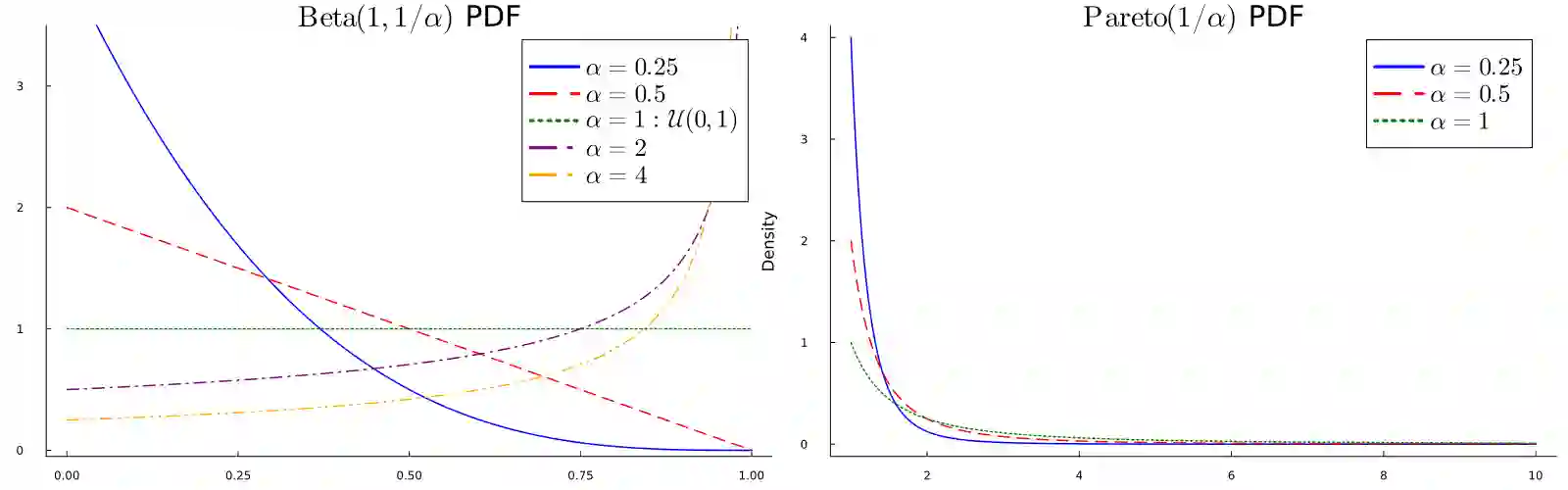
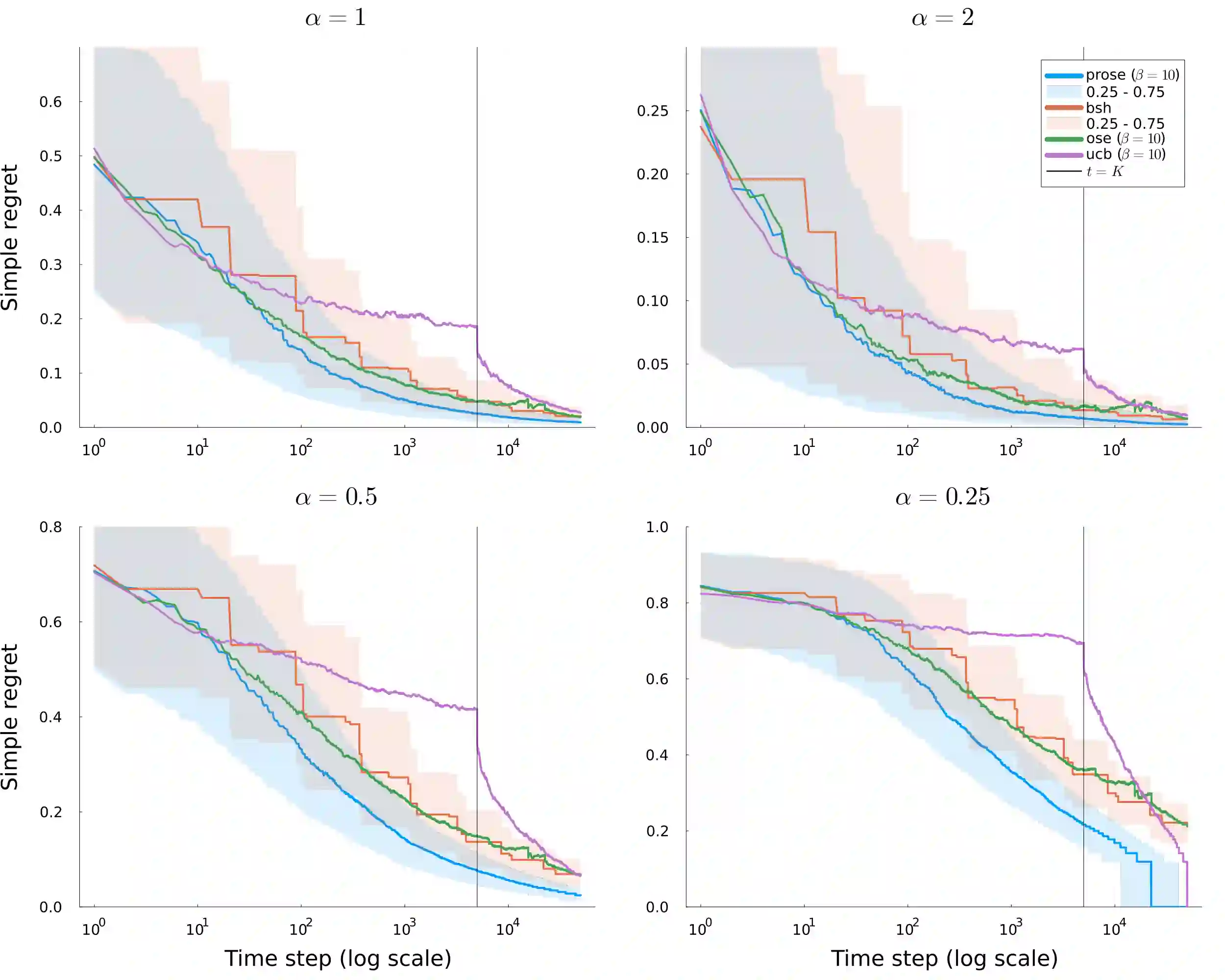
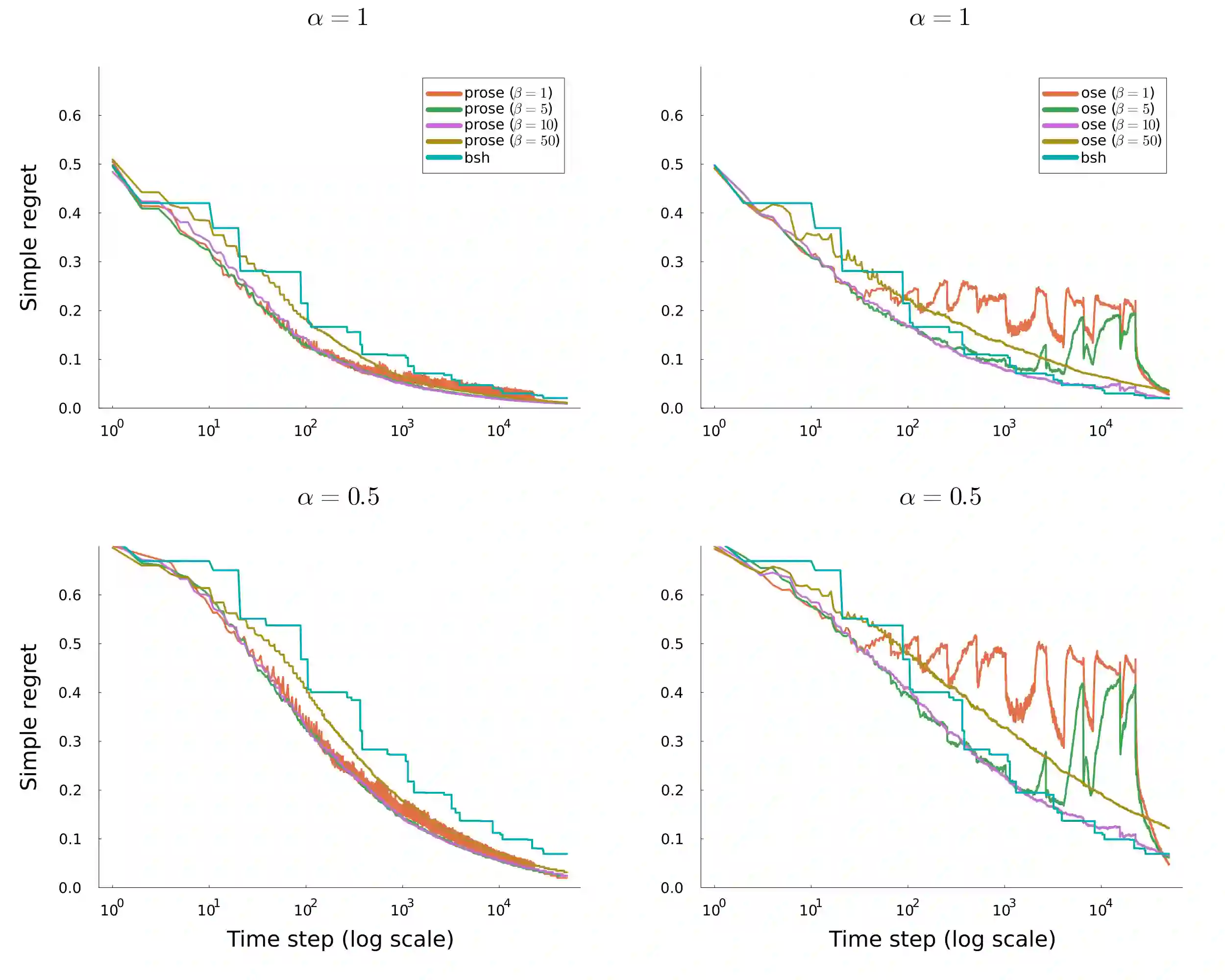
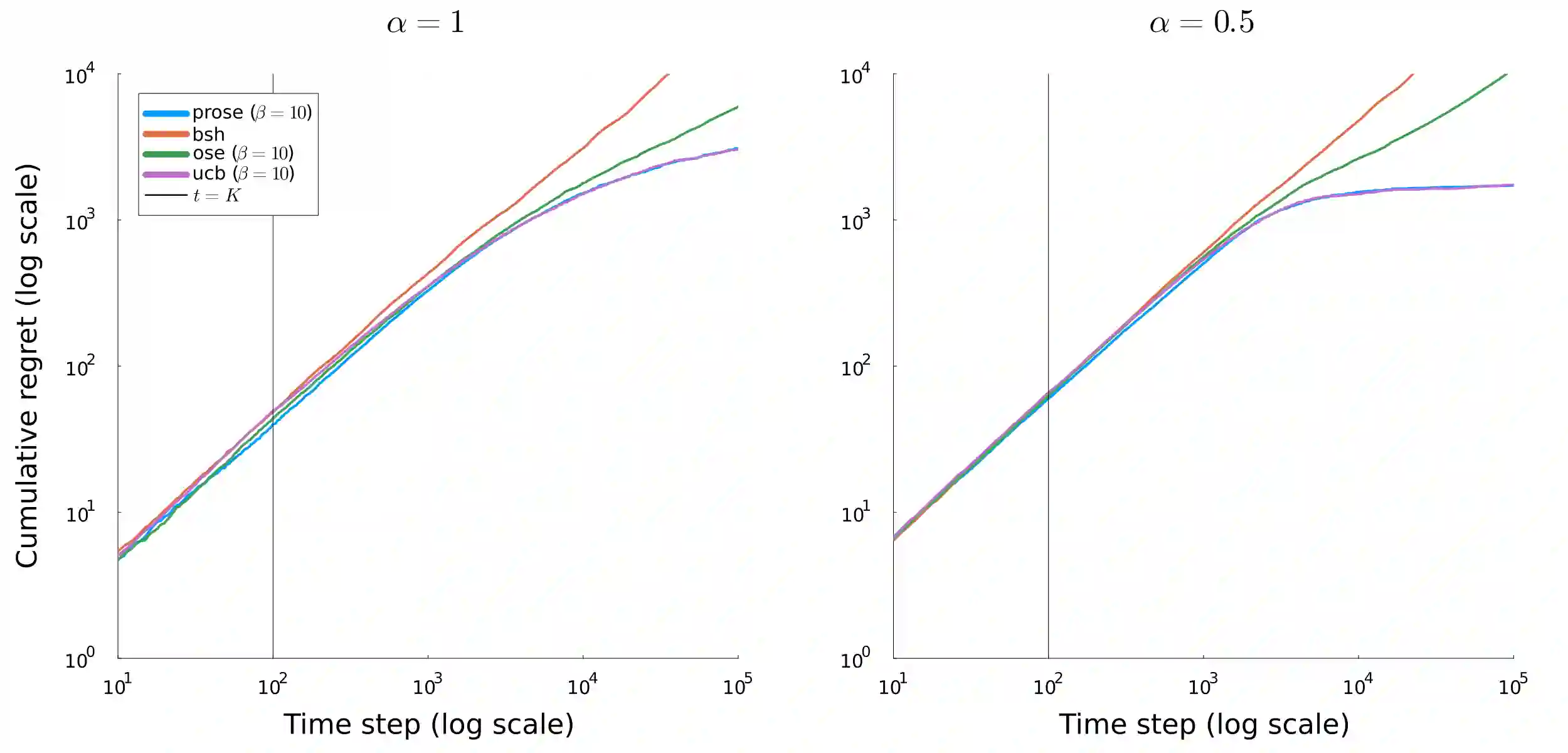
We consider a bandit problem where the buget is smaller than the number of arms, which may be infinite. In this regime, the usual objective in the literature is to minimize simple regret. To analyze broad classes of distributions with potentially unbounded support, where simple regret may not be well-defined, we take a slightly different approach and seek to maximize the expected simple reward of the recommended arm, providing anytime guarantees. To that end, we introduce a distribution-free algorithm, OSE, that adapts to the distribution of arm means and achieves near-optimal rates for several distribution classes. We characterize the sample complexity through the rank-corrected inverse squared gap function. In particular, we recover known upper bounds and transition regimes for $\alpha$ less or greater than $1/2$ when the quantile function is $\lambda_\eta = 1-\eta^{1/\alpha}$. We additionally identify new transition regimes depending on the noise level relative to $\alpha$, which we conjecture to be nearly optimal. Additionally, we introduce an enhanced practical version, PROSE, that achieves state-of-the-art empirical performance for the main distribution classes considered in the literature.

翻译：我们考虑一个预算小于臂数量的老虎机问题，其中臂的数量可能为无限。在此设定下，文献中通常的目标是最小化简单遗憾。为了分析具有潜在无界支撑的广泛分布类别（其中简单遗憾可能无法明确定义），我们采用略有不同的方法，旨在最大化推荐臂的期望简单奖励，并提供任意时间保证。为此，我们提出了一种与分布无关的算法OSE，该算法能够自适应臂均值的分布，并在多个分布类别中实现接近最优的收敛速率。我们通过秩校正逆平方间隙函数来刻画样本复杂度。特别地，当分位数函数为λ_η = 1-η^{1/α}时，我们恢复了α小于或大于1/2情况下的已知上界和过渡机制。此外，我们还识别了取决于噪声水平相对于α的新过渡机制，我们推测这些机制接近最优。另外，我们提出了一种增强的实用版本PROSE，该版本在文献中考虑的主要分布类别上实现了最先进的实证性能。