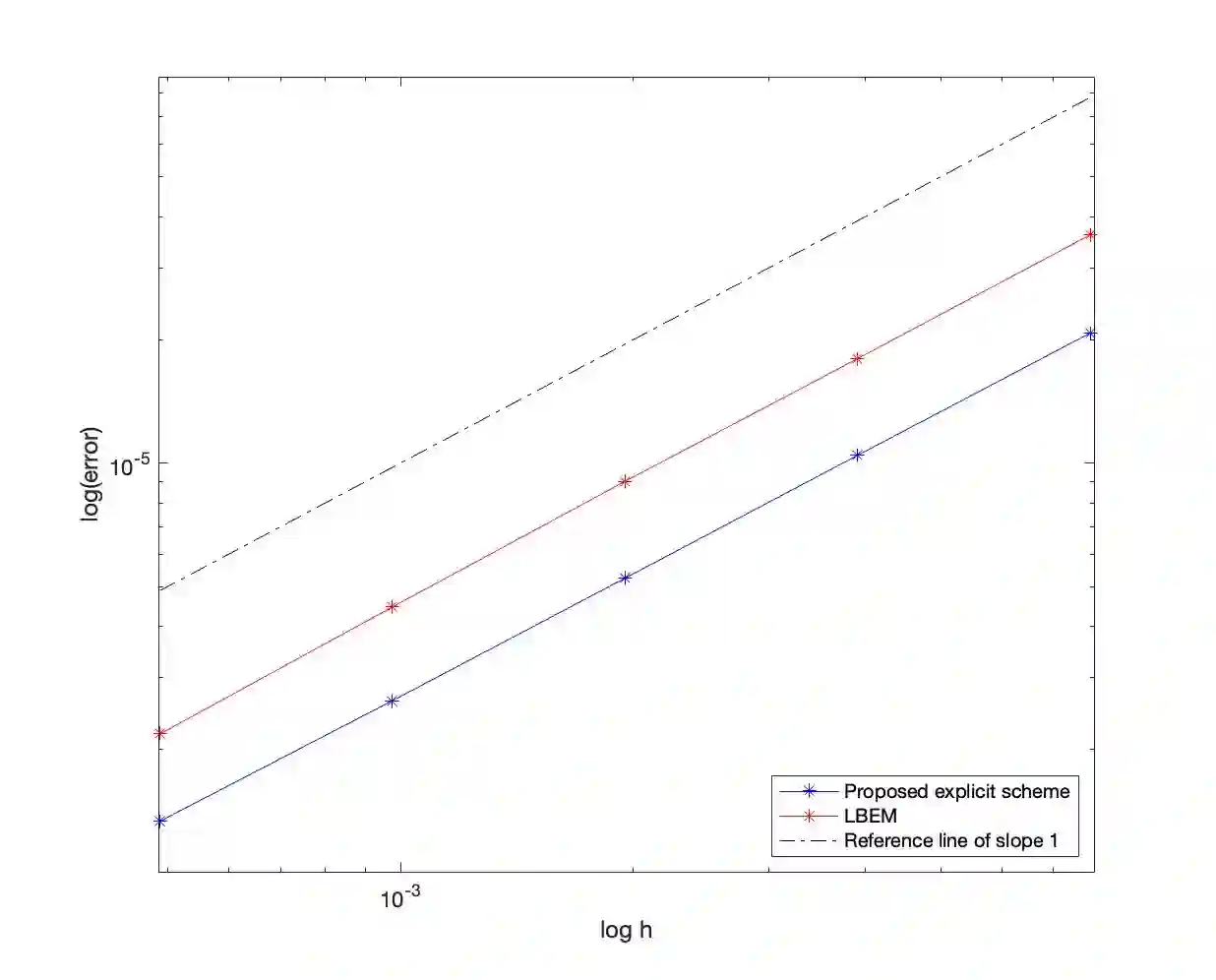
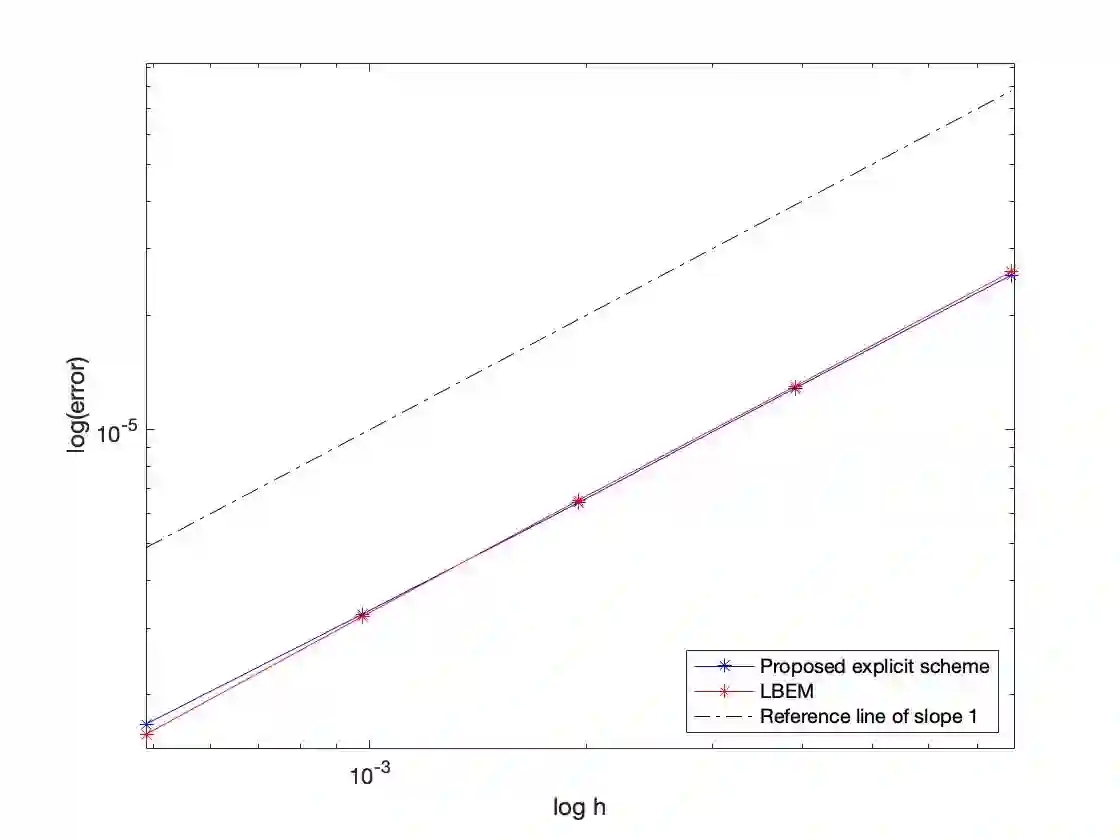
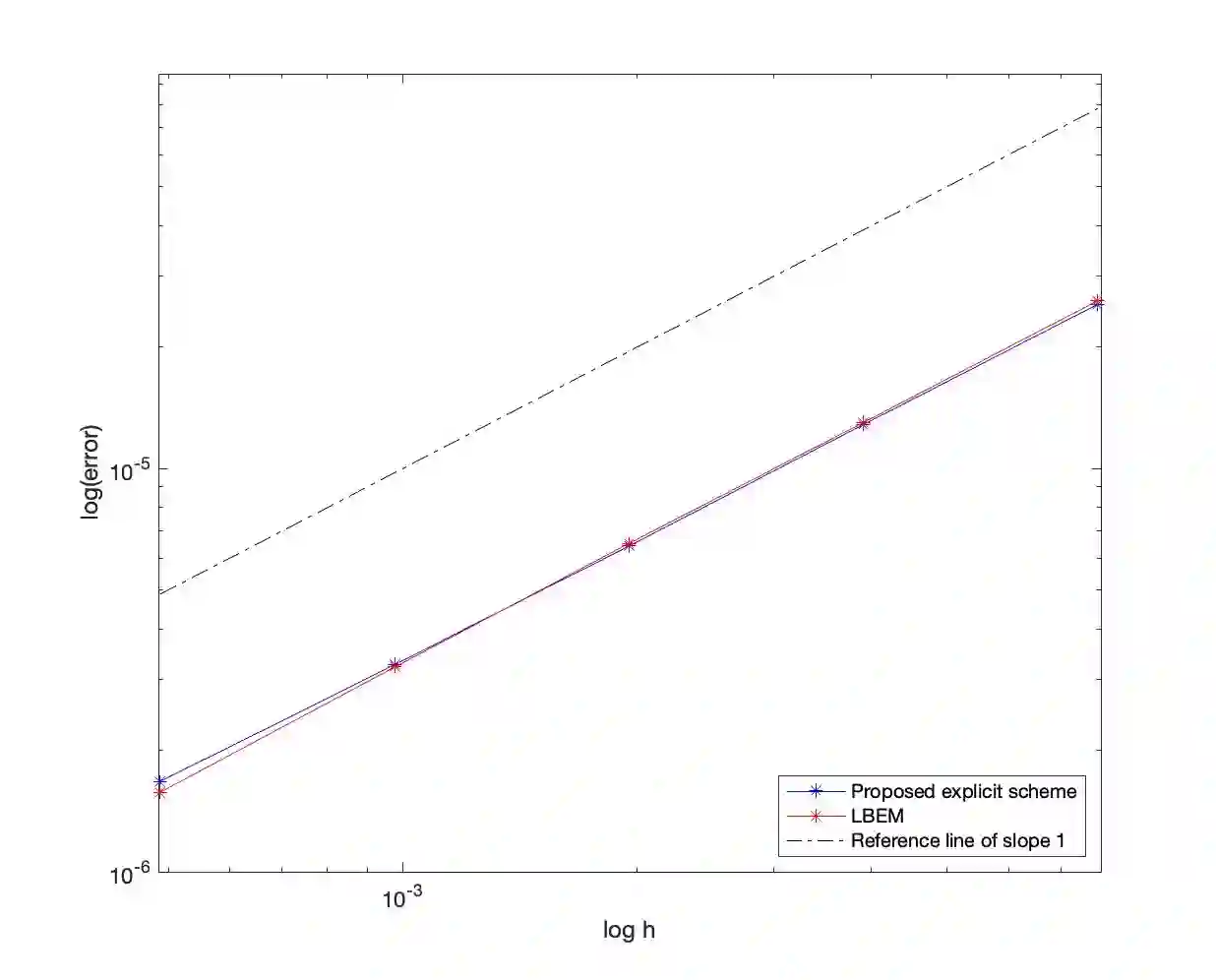
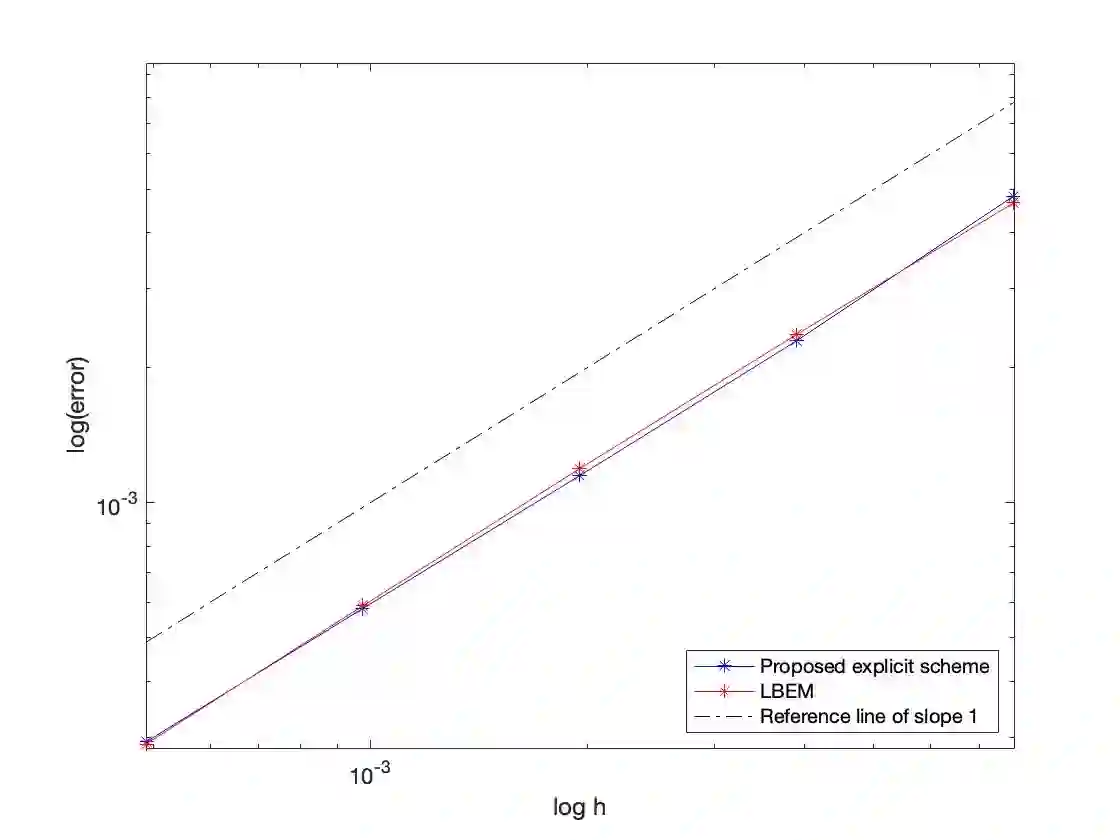
In this paper, we are interested in positivity-preserving approximations of stochastic differential equations (SDEs) with non-Lipschitz coefficients, arising from computational finance and possessing positive solutions. By leveraging a Lamperti transformation, we develop a novel, explicit, and unconditionally positivity-preserving numerical scheme for the considered financial SDEs. More precisely, an implicit term $c_{-1}Y_{n+1}^{-1}$ is incorporated in the scheme to guarantee unconditional positivity preservation, and a corrective operator is introduced in the remaining explicit terms to address the challenges posed by non-Lipschitz (possibly singular) coefficients of the transformed SDEs. By finding a unique positive root of a quadratic equation, the proposed scheme can be explicitly solved and is shown to be strongly convergent with order $1$, when used to numerically solve several well-known financial models such as the CIR process, the Heston-3/2 volatility model, the CEV process and the A\"it-Sahalia model. Numerical experiments validate the theoretical findings.

翻译：本文研究计算金融领域中具有非Lipschitz系数且解保持正性的随机微分方程(SDEs)的保正逼近方法。通过利用Lamperti变换，我们为所考虑的金融随机微分方程构建了一种新颖的显式且无条件保持正性的数值格式。具体而言，该格式引入隐式项$c_{-1}Y_{n+1}^{-1}$以保证无条件正性保持，同时在其余显式项中引入校正算子以应对变换后随机微分方程非Lipschitz（可能奇异）系数带来的挑战。通过求解二次方程的唯一正根，所提格式可显式求解，并在数值求解CIR过程、Heston-3/2波动率模型、CEV过程及Aït-Sahalia模型等经典金融模型时，被证明具有一阶强收敛性。数值实验验证了理论结果。