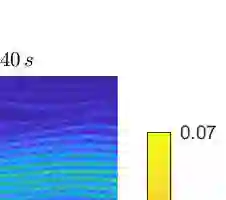
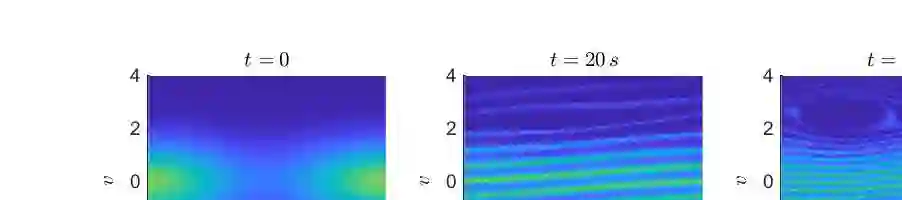
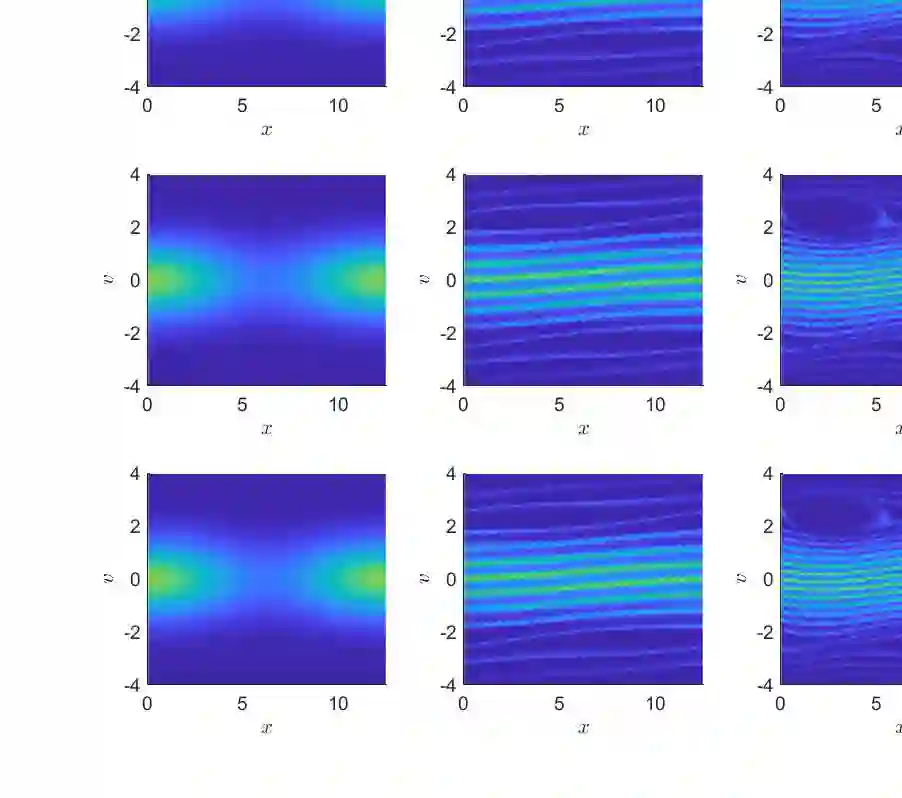
This paper proposes an adaptive hyper-reduction method to reduce the computational cost associated with the simulation of parametric particle-based kinetic plasma models, specifically focusing on the Vlasov-Poisson equation. Conventional model order reduction and hyper-reduction techniques are often ineffective for such models due to the non-sparse nature of the nonlinear operators arising from the interactions between particles. To tackle this issue, we propose an adaptive, structure-preserving hyper-reduction method that leverages a decomposition of the discrete reduced Hamiltonian into a linear combination of terms, each depending on a few components of the state. The proposed approximation strategy allows to: (i) preserve the Hamiltonian structure of the problem; (ii) evaluate nonlinear non-sparse operators in a computationally efficient way; (iii) overcome the Kolmogorov barrier of transport-dominated problems via evolution of the approximation space and adaptivity of the rank of the solution. The proposed method is validated on numerical benchmark simulations, demonstrating stable and accurate performance with substantial runtime reductions compared to the full order model.

翻译：本文提出了一种自适应超约简方法，旨在降低参数化粒子基动理学等离子体模型（特别聚焦于Vlasov-Poisson方程）模拟相关的计算成本。传统的模型降阶与超约简技术对此类模型往往效果有限，原因在于粒子间相互作用产生的非线性算子具有非稀疏特性。为解决此问题，我们提出一种自适应、保结构的超约简方法，该方法利用离散约化哈密顿量分解为若干项的线性组合，其中每一项仅依赖于状态的少数分量。所提出的近似策略能够：（i）保持问题的哈密顿结构；（ii）以计算高效的方式评估非线性非稀疏算子；（iii）通过近似空间的演化与解秩的自适应性，突破以输运为主导问题的Kolmogorov障碍。通过对数值基准模拟的验证，该方法展现出稳定且精确的性能，与全阶模型相比实现了显著的计算时间缩减。