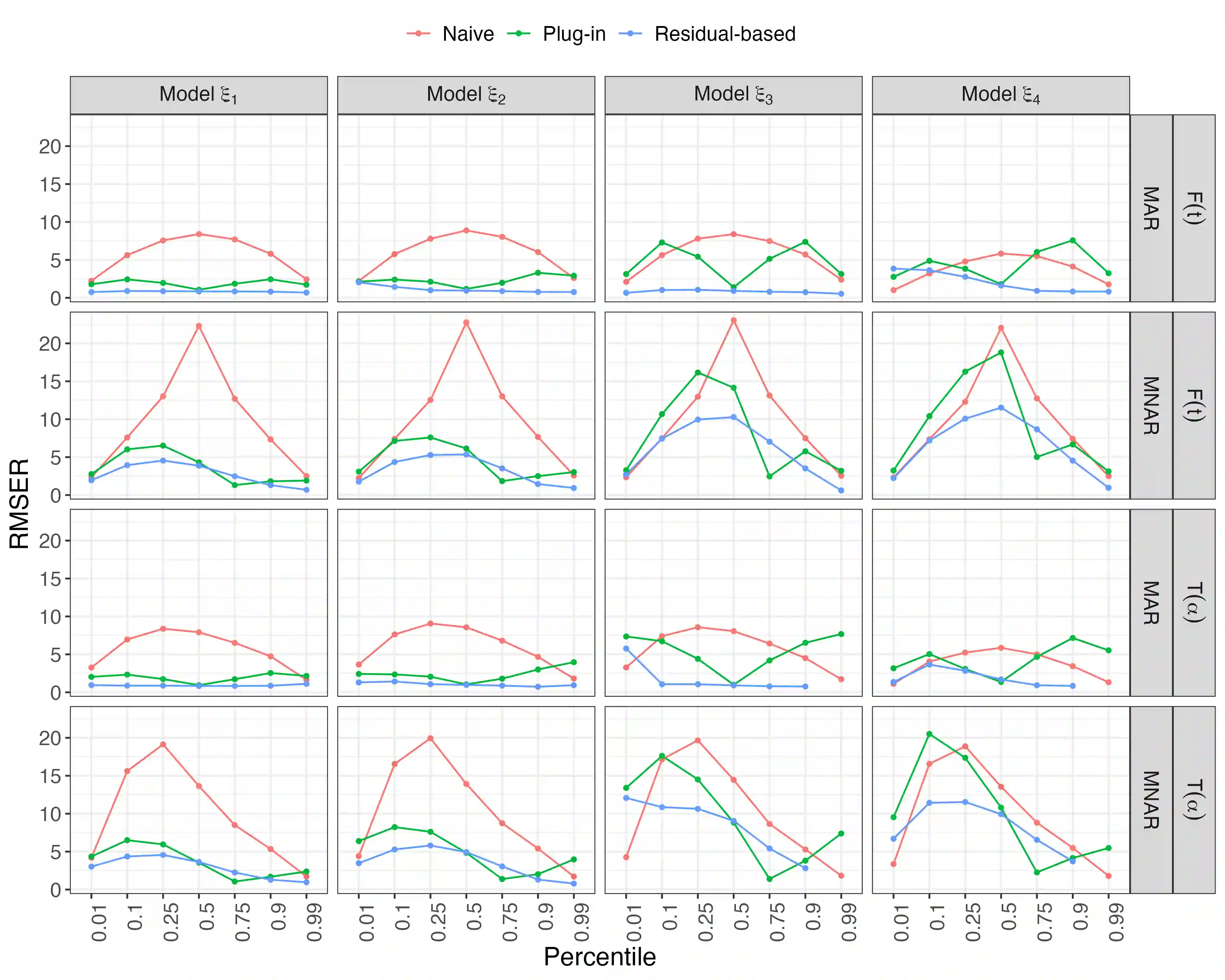
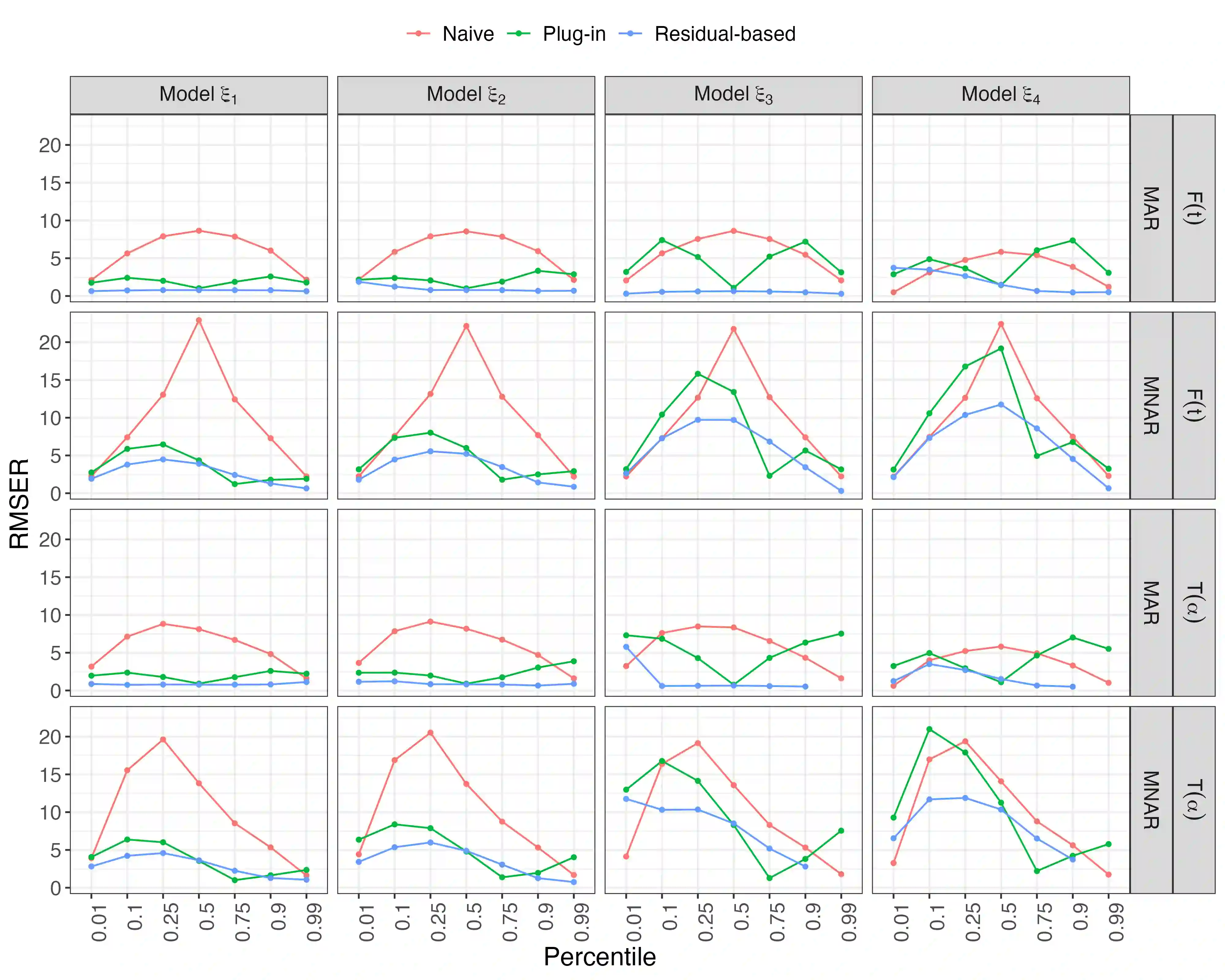
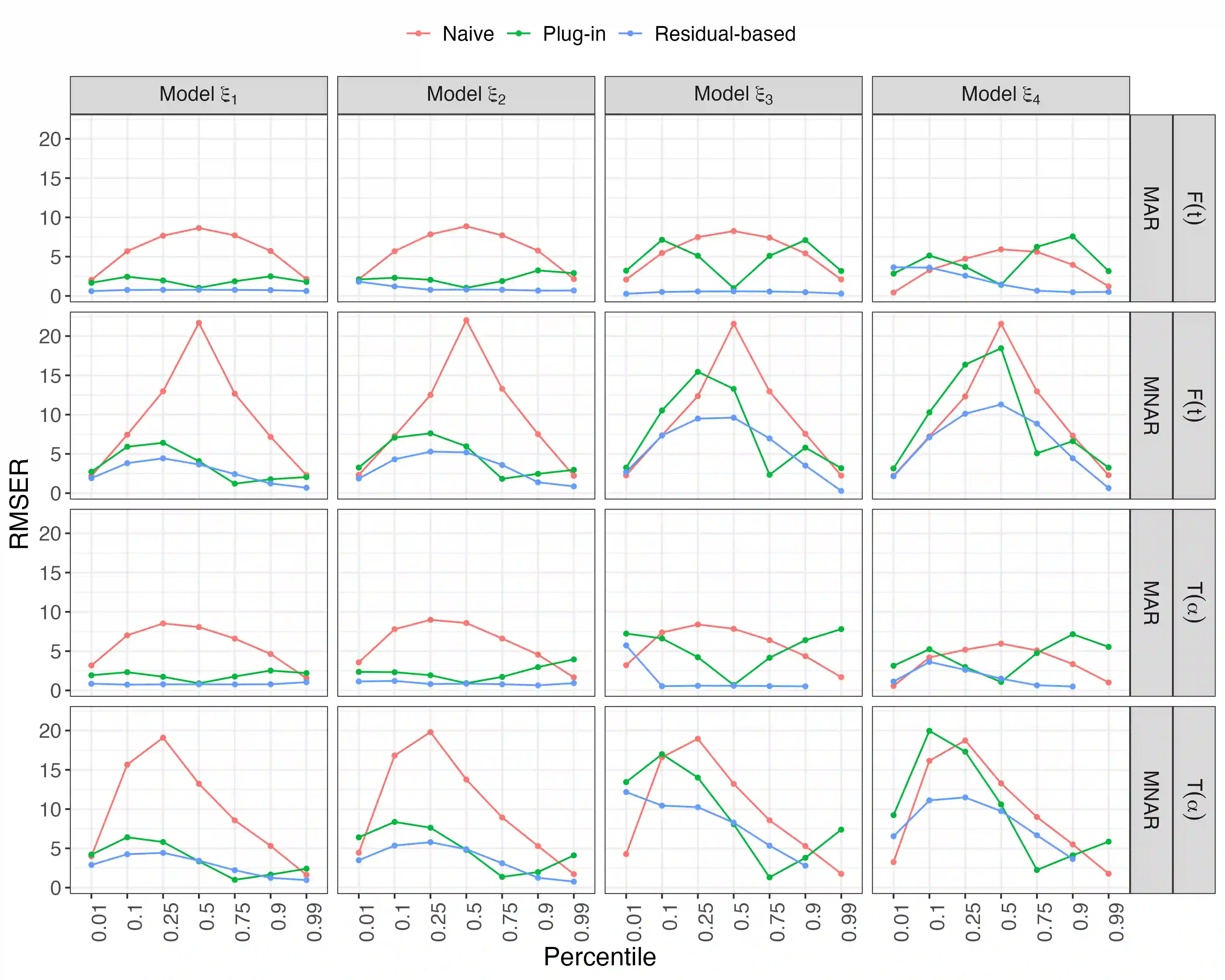
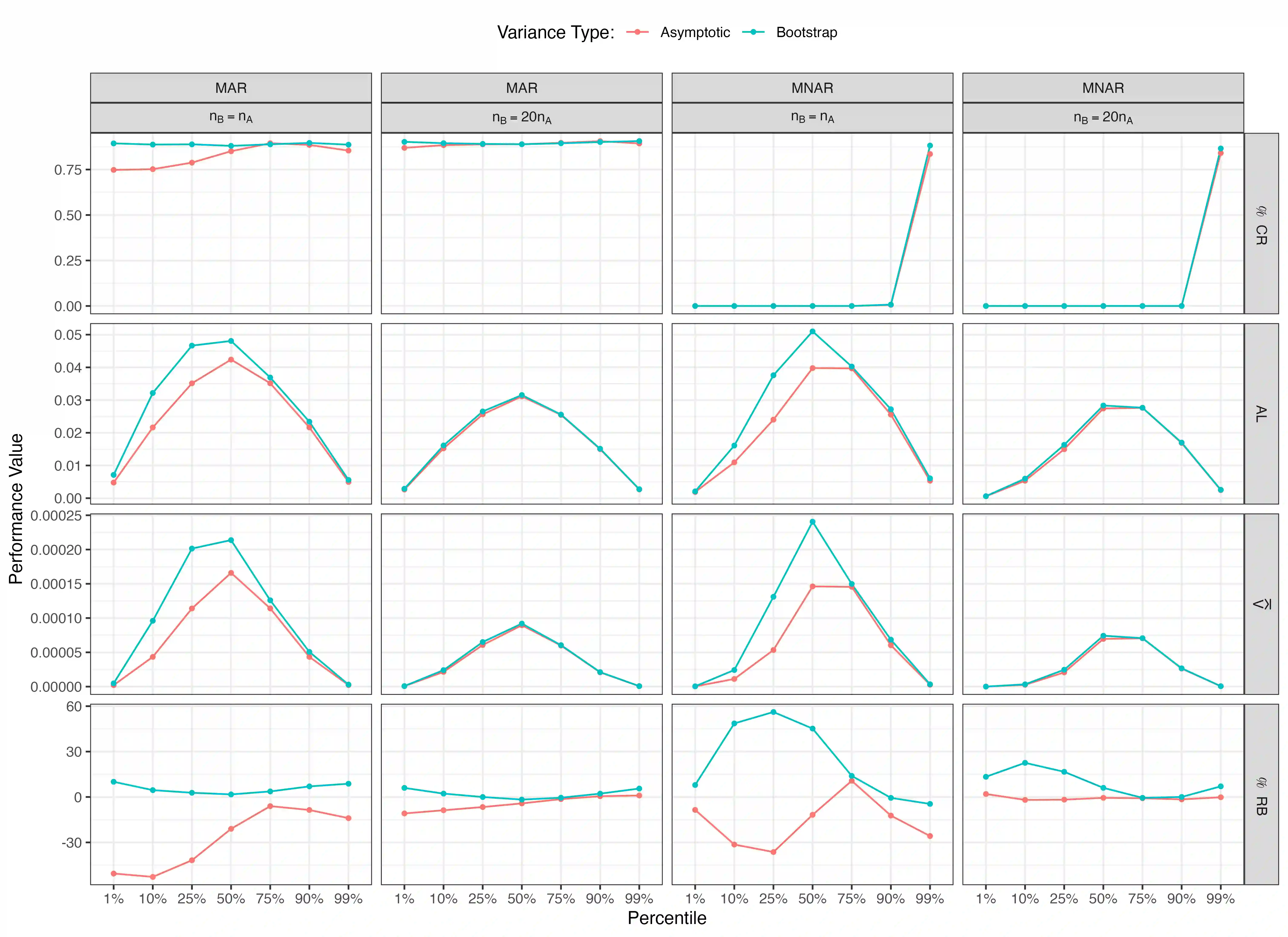
Estimates of finite population cumulativedistribution functions (CDFs) and quantiles are critical forpolicy-making, resource allocation, and public health planning. For instance, federal finance agencies may require accurate estimates of the proportion of individuals with income below the federal poverty line to determine funding eligibility, while health organizations may rely on precise quantile estimates of key health variables to guide local health interventions. Despite growing interest in survey data integration, research on the integration of probability and nonprobability samples toestimate CDFs and quantiles remains limited. In this study, we propose a novel residual-based CDF estimator that integrates information from a probability sample with data from potentially large nonprobability samples. Our approach leverages shared covariates observed in both datasets, while the response variable is available only in the nonprobability sample. Using a semiparametric approach, we train an outcome model on the nonprobability sample and incorporate model residuals with sampling weights from the probability sample to estimate the CDF of the target variable. Based on this CDF estimator, we define a quantile estimator and introduce linearization and bootstrap methods for variance estimation of both the CDF and quantile estimators. Under certain regularity conditions, we establish the asymptotic properties, including bias and variance, of the CDF estimator. Our empirical findings support the theoretical results and demonstrate the favorable performance of the proposed estimators relative to plug-in mass imputation estimators and the na\"ive estimators derived from the nonprobability sample only. A real data example is presented to illustrate the proposed estimators.

翻译：有限总体累积分布函数（CDF）与分位数的估计对于政策制定、资源分配和公共卫生规划至关重要。例如，联邦财政机构可能需要准确估计收入低于联邦贫困线的人口比例以确定资金发放资格，而卫生组织则可能依赖关键健康变量的精确分位数估计来指导地方卫生干预措施。尽管对调查数据整合的兴趣日益增长，但关于整合概率样本与非概率样本来估计CDF和分位数的研究仍较为有限。本研究提出一种新颖的基于残差的CDF估计器，该估计器整合了来自概率样本的信息与可能大规模的非概率样本数据。我们的方法利用两个数据集中共同观测到的协变量，而响应变量仅存在于非概率样本中。通过半参数方法，我们在非概率样本上训练结果模型，并将模型残差与概率样本的抽样权重相结合，以估计目标变量的CDF。基于此CDF估计器，我们定义了分位数估计器，并引入线性化与自助法用于CDF和分位数估计器的方差估计。在特定正则条件下，我们建立了CDF估计器的渐近性质，包括偏差与方差。实证结果支持理论结论，并证明所提估计器相较于基于插值的大规模填补估计器及仅从非概率样本导出的朴素估计器具有更优性能。文中通过实际数据案例展示了所提估计器的应用。