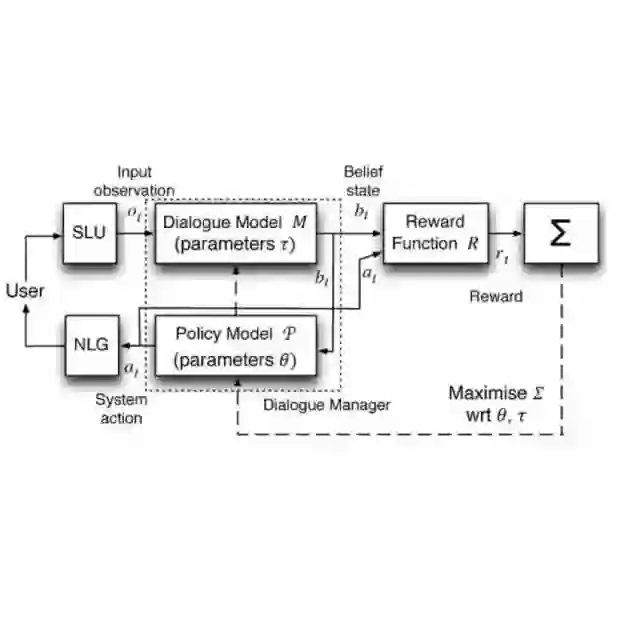
In many interactive decision-making settings, there is latent and unobserved information that remains fixed. Consider, for example, a dialogue system, where complete information about a user, such as the user's preferences, is not given. In such an environment, the latent information remains fixed throughout each episode, since the identity of the user does not change during an interaction. This type of environment can be modeled as a Latent Markov Decision Process (LMDP), a special instance of Partially Observed Markov Decision Processes (POMDPs). Previous work established exponential lower bounds in the number of latent contexts for the LMDP class. This puts forward a question: under which natural assumptions a near-optimal policy of an LMDP can be efficiently learned? In this work, we study the class of LMDPs with {\em prospective side information}, when an agent receives additional, weakly revealing, information on the latent context at the beginning of each episode. We show that, surprisingly, this problem is not captured by contemporary settings and algorithms designed for partially observed environments. We then establish that any sample efficient algorithm must suffer at least $\Omega(K^{2/3})$-regret, as opposed to standard $\Omega(\sqrt{K})$ lower bounds, and design an algorithm with a matching upper bound.

翻译：暂无翻译