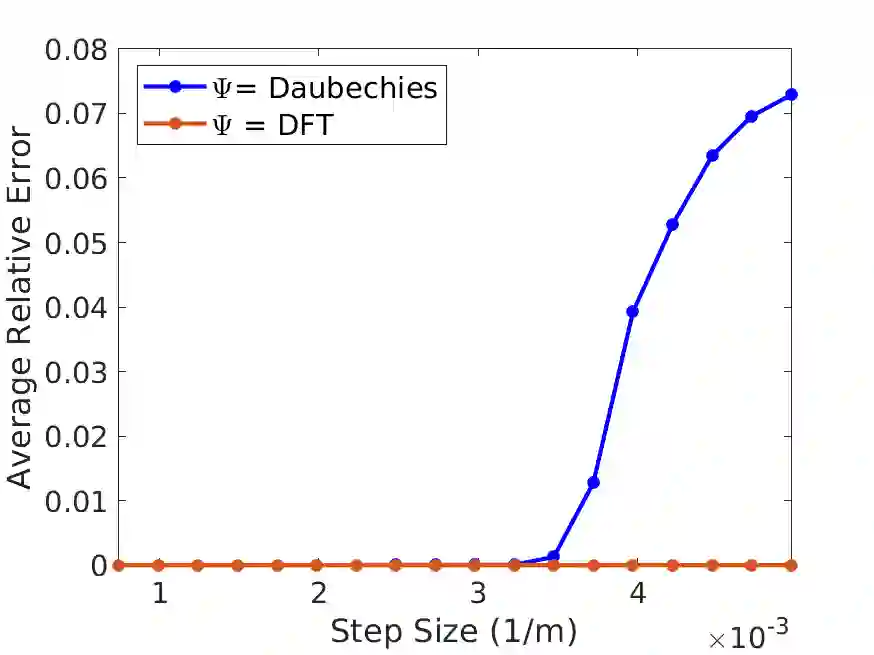
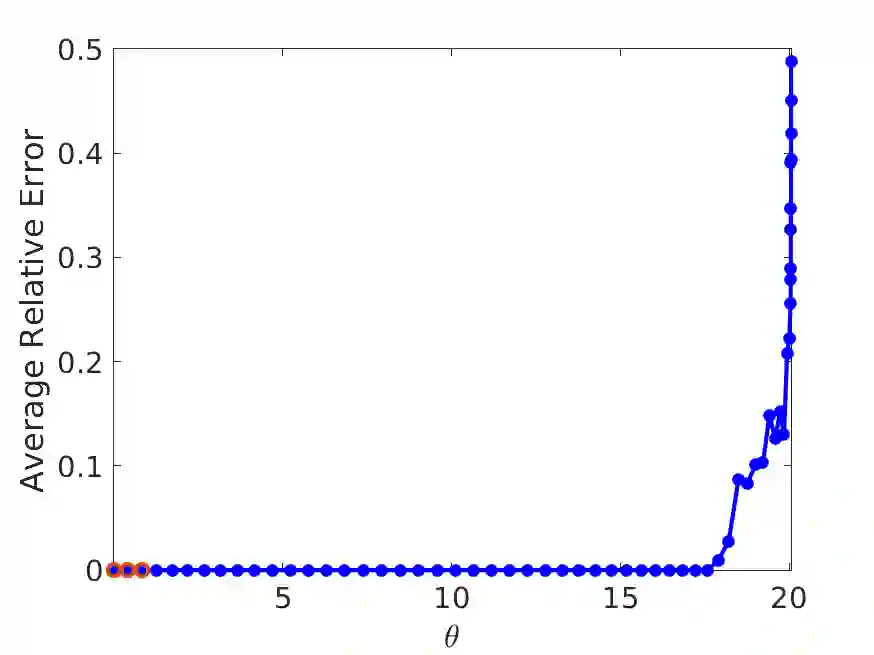
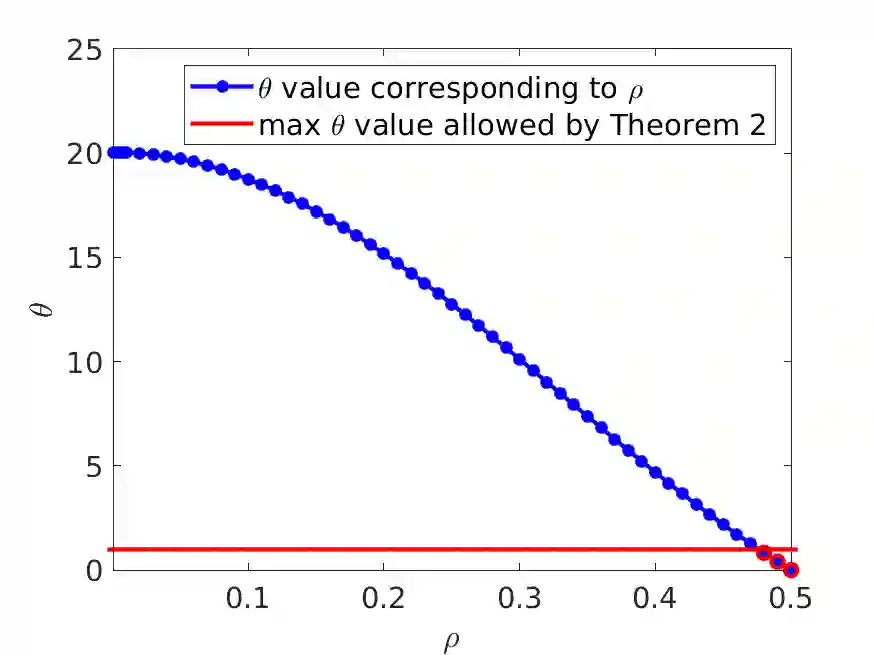
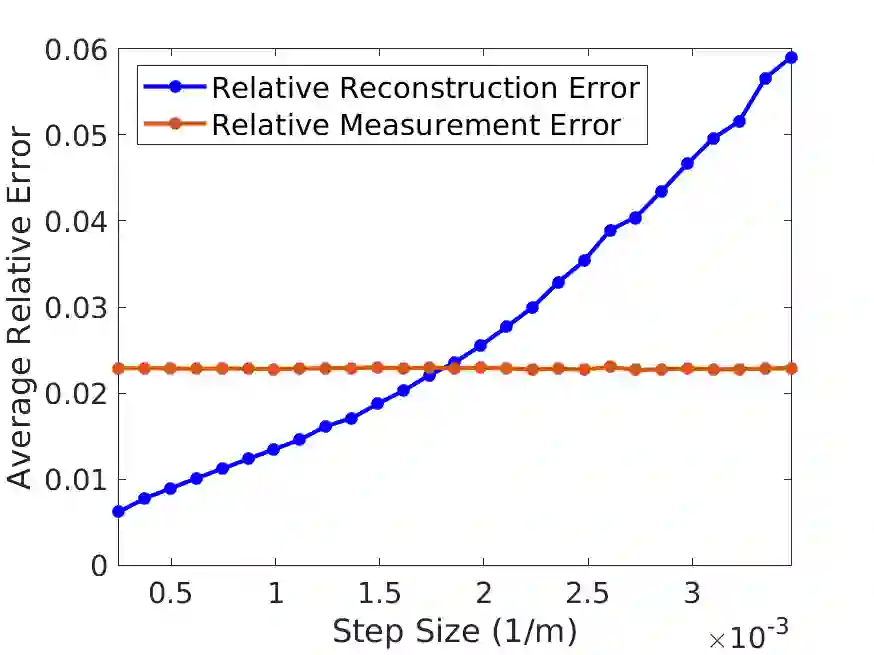
Many empirical studies suggest that samples of continuous-time signals taken at locations randomly deviated from an equispaced grid (i.e., off-the-grid) can benefit signal acquisition, e.g., undersampling and anti-aliasing. However, explicit statements of such advantages and their respective conditions are scarce in the literature. This paper provides some insight on this topic when the sampling positions are known, with grid deviations generated i.i.d. from a variety of distributions. By solving a square-root LASSO decoder with an interpolation kernel we demonstrate the capabilities of nonuniform samples for compressive sampling, an effective paradigm for undersampling and anti-aliasing. For functions in the Wiener algebra that admit a discrete $s$-sparse representation in some transform domain, we show that $\mathcal{O}(s\log N)$ random off-the-grid samples are sufficient to recover an accurate $\frac{N}{2}$-bandlimited approximation of the signal. For sparse signals (i.e., $s \ll N$), this sampling complexity is a great reduction in comparison to equispaced sampling where $\mathcal{O}(N)$ measurements are needed for the same quality of reconstruction (Nyquist-Shannon sampling theorem). We further consider noise attenuation via oversampling (relative to a desired bandwidth), a standard technique with limited theoretical understanding when the sampling positions are non-equispaced. By solving a least squares problem, we show that $\mathcal{O}(N\log N)$ i.i.d. randomly deviated samples provide an accurate $\frac{N}{2}$-bandlimited approximation of the signal with suppression of the noise energy by a factor $\sim\frac{1}{\sqrt{\log N}}$.

翻译：许多实证研究表明,在随机偏离位置上采集的连续时间信号样本可以有利于信号获取,例如,低采样和反丑闻。然而,文献中缺乏关于这些优势及其各自条件的明确陈述。本文在取样位置已知时提供了对这一主题的一些洞察力,从各种分布中生成了i.d. 网格偏差。通过解决一个平方根的LASSO解码器和内核内核,我们展示了用于压缩采样的非单式样品的能力,例如,低采样和反丑闻的有效范例。对于维纳变域中承认离合美元代表的功能,我们显示,由于随机离网样品的离网值值(s\log N),因此可以恢复准确的 美元-(sercox) 内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内 内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核内核