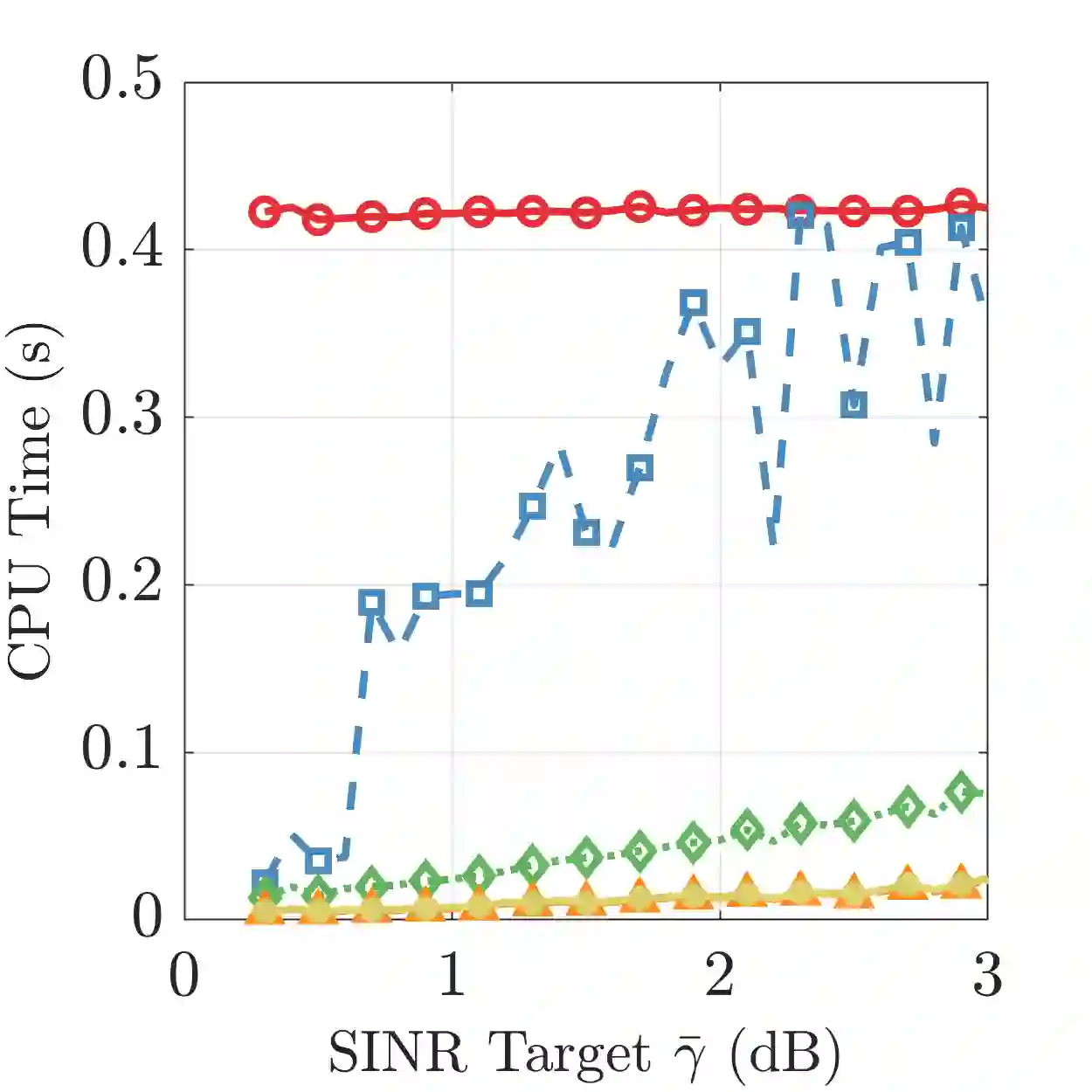
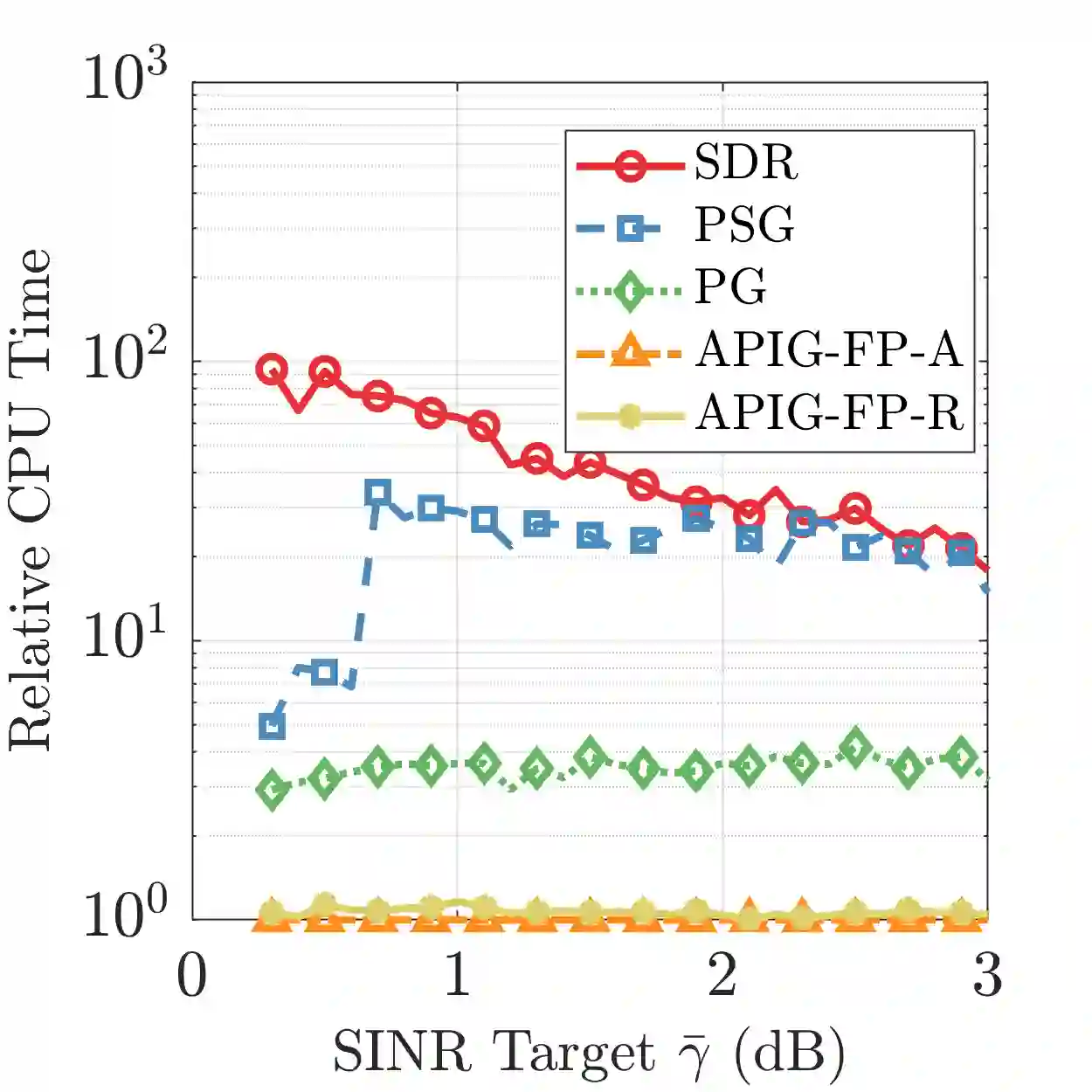
In this paper, we propose an adaptive proximal inexact gradient (APIG) framework for solving a class of nonsmooth composite optimization problems involving function and gradient errors. Unlike existing inexact proximal gradient methods, the proposed framework introduces a new line search condition that jointly adapts to function and gradient errors, enabling adaptive stepsize selection while maintaining theoretical guarantees. Specifically, we prove that the proposed framework achieves an $\epsilon$-stationary point within $\mathcal{O}(\epsilon^{-2})$ iterations for nonconvex objectives and an $\epsilon$-optimal solution within $\mathcal{O}(\epsilon^{-1})$ iterations for convex cases, matching the best-known complexity in this context. We then custom-apply the APIG framework to an important signal processing problem: the joint beamforming and compression problem (JBCP) with per-antenna power constraints (PAPCs) in cooperative cellular networks. This customized application requires careful exploitation of the problem's special structure such as the tightness of the semidefinite relaxation (SDR) and the differentiability of the dual. Numerical experiments demonstrate the superior performance of our custom-application over state-of-the-art benchmarks for the JBCP.

翻译：本文提出了一种自适应近端非精确梯度（APIG）框架，用于求解一类涉及函数与梯度误差的非光滑复合优化问题。与现有的非精确近端梯度方法不同，所提框架引入了一种新的线搜索条件，该条件能同时适应函数与梯度误差，从而在保持理论保证的同时实现自适应步长选择。具体而言，我们证明了对于非凸目标，该框架可在 $\mathcal{O}(\epsilon^{-2})$ 次迭代内达到 $\epsilon$-稳定点；对于凸情形，可在 $\mathcal{O}(\epsilon^{-1})$ 次迭代内获得 $\epsilon$-最优解，与此情境下已知的最佳复杂度相匹配。随后，我们将APIG框架定制应用于一个重要的信号处理问题：协作蜂窝网络中具有每天线功率约束（PAPCs）的联合波束成形与压缩问题（JBCP）。此定制应用需要仔细利用问题的特殊结构，例如半定松弛（SDR）的紧致性以及对偶问题的可微性。数值实验表明，针对JBCP问题，我们的定制应用相较于现有先进基准方法具有更优越的性能。