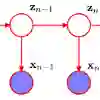
Hidden Markov models (HMMs) are characterized by an unobservable Markov chain and an observable process -- a noisy version of the hidden chain. Decoding the original signal from the noisy observations is one of the main goals in nearly all HMM based data analyses. Existing decoding algorithms such as Viterbi and the pointwise maximum a posteriori (PMAP) algorithm have computational complexity at best linear in the length of the observed sequence, and sub-quadratic in the size of the state space of the hidden chain. We present Quick Adaptive Ternary Segmentation (QATS), a divide-and-conquer procedure with computational complexity polylogarithmic in the length of the sequence, and cubic in the size of the state space, hence particularly suited for large scale HMMs with relatively few states. It also suggests an effective way of data storage as specific cumulative sums. In essence, the estimated sequence of states sequentially maximizes local likelihood scores among all local paths with at most three segments, and is meanwhile admissible. The maximization is performed only approximately using an adaptive search procedure. Our simulations demonstrate the speedups offered by QATS in comparison to Viterbi and PMAP, along with a precision analysis. An implementation of QATS is in the R-package QATS on GitHub.

翻译：隐马尔可夫模型（HMM）由一个不可观测的马尔可夫链和一个可观测过程（即隐藏链的噪声版本）所刻画。从含噪声的观测中解码原始信号是几乎所有基于HMM的数据分析的主要目标之一。现有的解码算法（如维特比算法和逐点最大后验概率算法）的计算复杂度在观测序列长度上至少为线性，在隐藏链状态空间大小上为次二次方。本文提出快速自适应三元分割（QATS），这是一种分治算法，其计算复杂度在序列长度上为多对数级，在状态空间大小上为三次方，因此特别适用于状态数相对较少的大规模HMM。该方法还提出了一种基于特定累积和的有效数据存储方式。本质上，估计的状态序列在所有至多包含三个分段的局部路径中顺序地最大化局部似然得分，同时满足可容许性。该最大化过程仅通过一种自适应搜索算法近似实现。我们的仿真实验展示了QATS相较于维特比算法和逐点最大后验概率算法所提供的速度优势，并进行了精度分析。QATS的实现代码位于GitHub上的R软件包QATS中。