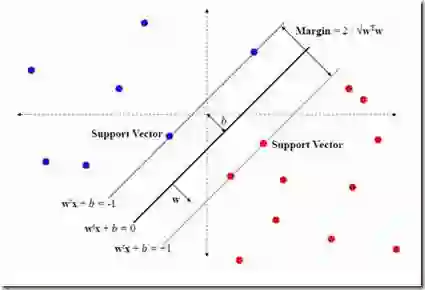
We study the problem of computing an $ε$-approximate Nash equilibrium of a two-player, bilinear, zero-sum game with a bounded payoff matrix $A \in \mathbb{R}^{m \times n}$, when the players' strategies are constrained to lie in simple sets. We provide algorithms which solve this problem in $\tilde{O}(ε^{-2/3})$ matrix-vector multiplies (matvecs) in two well-studied cases: $\ell_1$-$\ell_1$ games, where the players' strategies are both in the probability simplex, and $\ell_2$-$\ell_1$ games, where the players' strategies are in the unit Euclidean ball and probability simplex respectively. These results improve upon the previous state-of-the-art complexities of $\tilde{O}(ε^{-8/9})$ for $\ell_1$-$\ell_1$ and of $\tilde{O}(ε^{-7/9})$ for $\ell_2$-$\ell_1$ due to [KOS '25]. In particular, our result for $\ell_2$-$\ell_1$, which corresponds to hard-margin support vector machines (SVMs), matches the lower bound of [KS '25] up to polylogarithmic factors.

翻译：我们研究在玩家策略被限制于简单集合内时，计算具有有界收益矩阵 $A \in \mathbb{R}^{m \times n}$ 的两人、双线性、零和博弈的 $ε$-近似纳什均衡问题。我们在两个经过充分研究的案例中提供了在 $\tilde{O}(ε^{-2/3})$ 次矩阵-向量乘法（matvecs）内解决此问题的算法：$\ell_1$-$\ell_1$ 博弈（双方策略均在概率单纯形中）和 $\ell_2$-$\ell_1$ 博弈（双方策略分别在单位欧几里得球和概率单纯形中）。这些结果改进了先前由 [KOS '25] 提出的 $\ell_1$-$\ell_1$ 博弈 $\tilde{O}(ε^{-8/9})$ 和 $\ell_2$-$\ell_1$ 博弈 $\tilde{O}(ε^{-7/9})$ 的最优复杂度。特别地，我们关于 $\ell_2$-$\ell_1$ 博弈（对应于硬间隔支持向量机（SVM））的结果，在多项式对数因子内匹配了 [KS '25] 给出的下界。