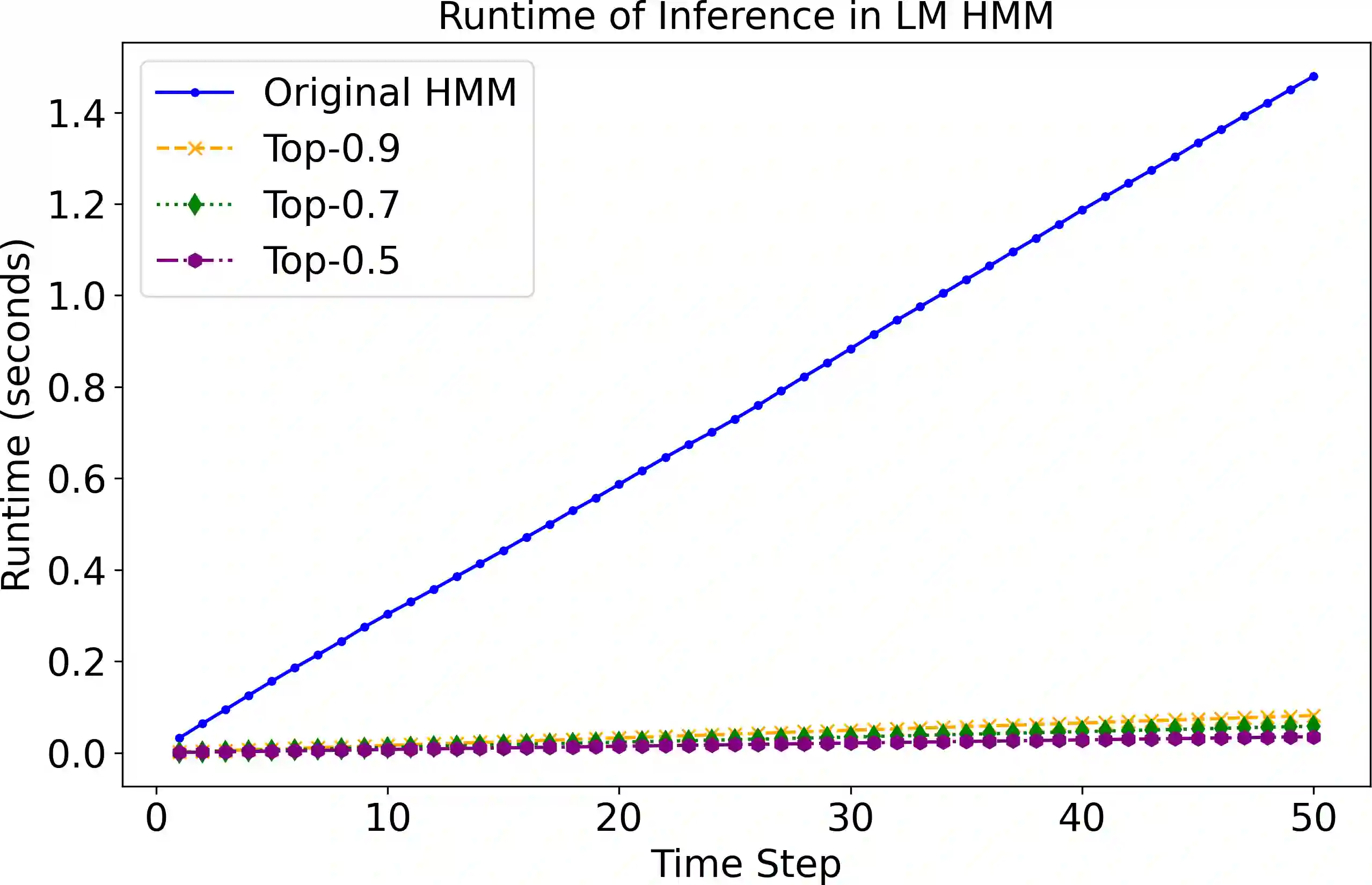
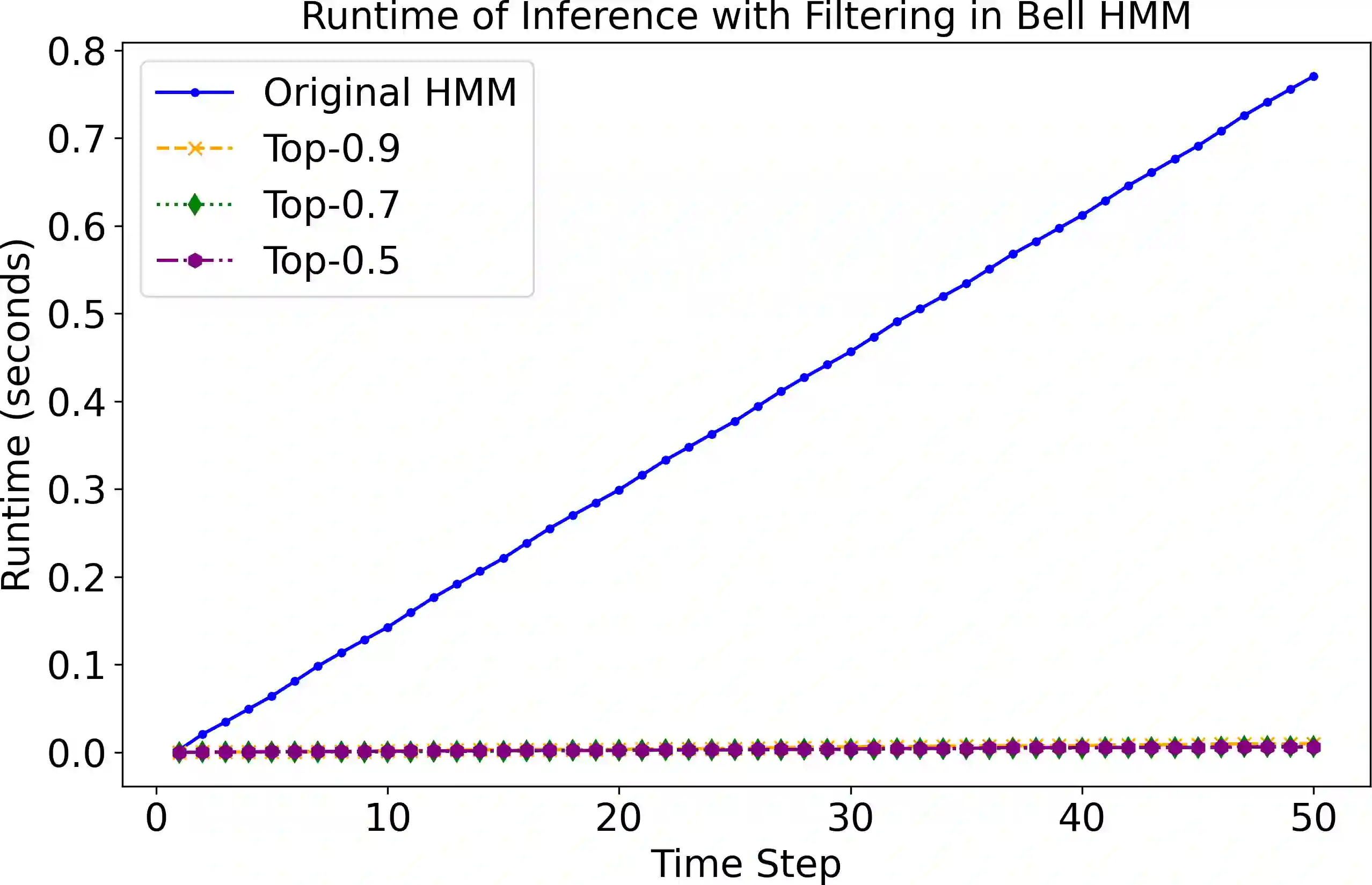
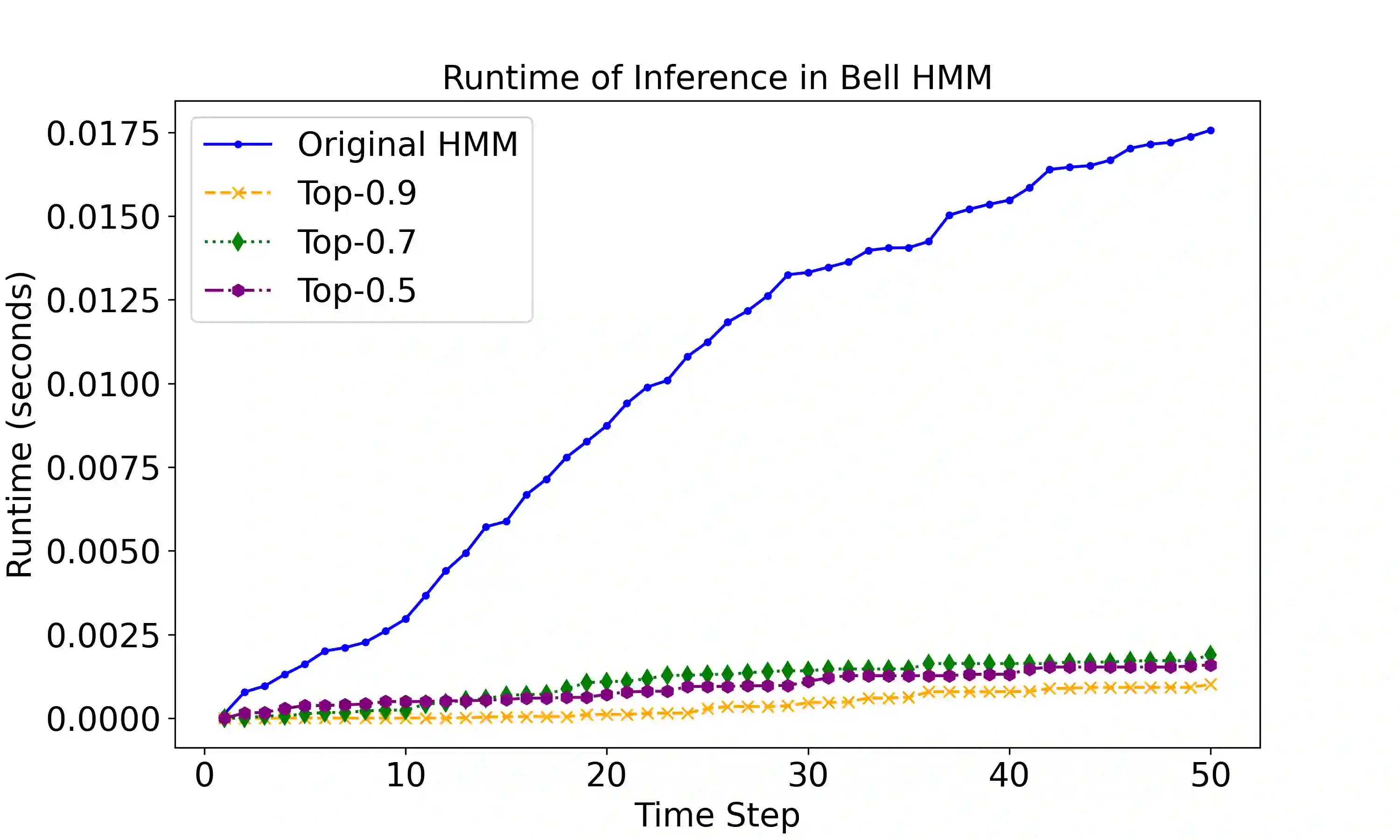
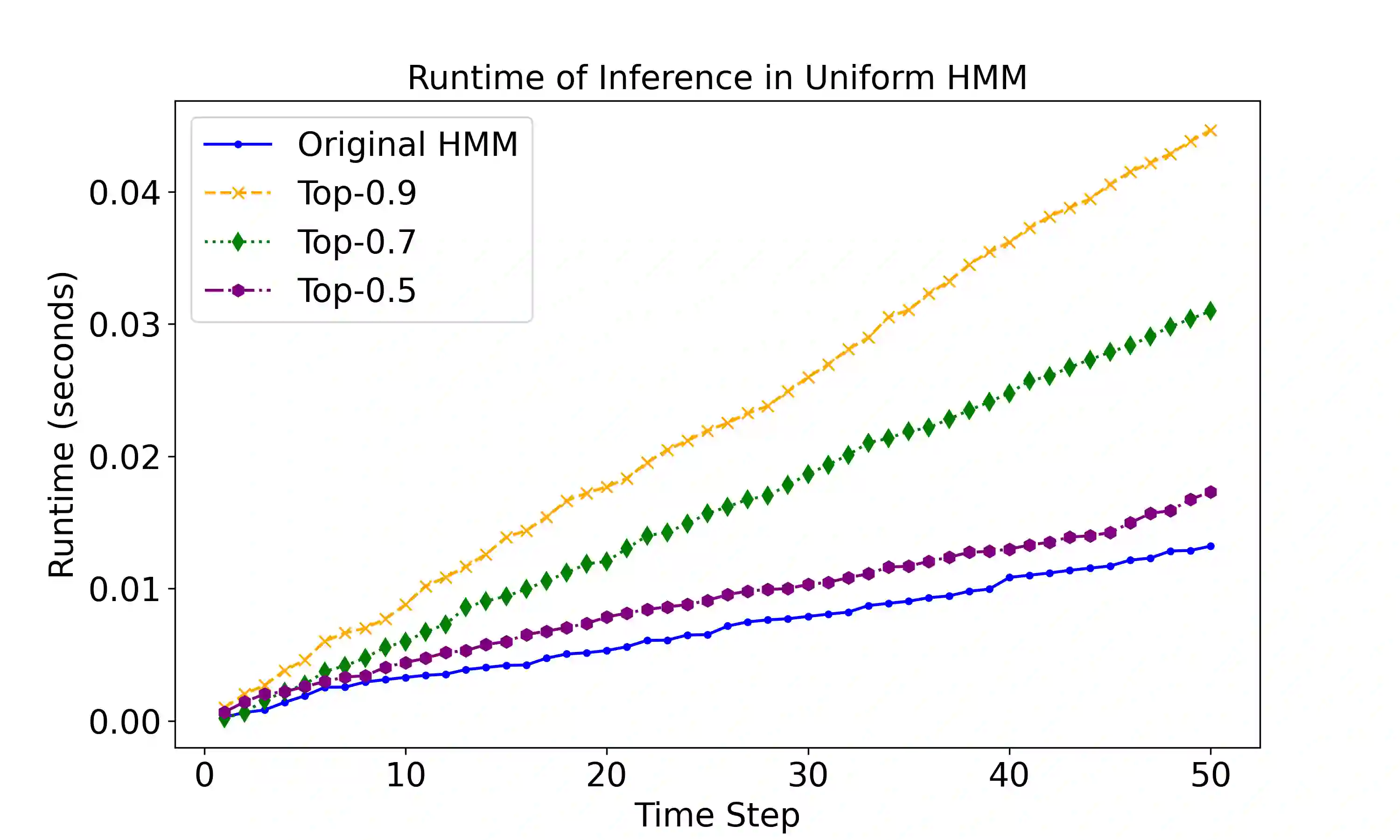
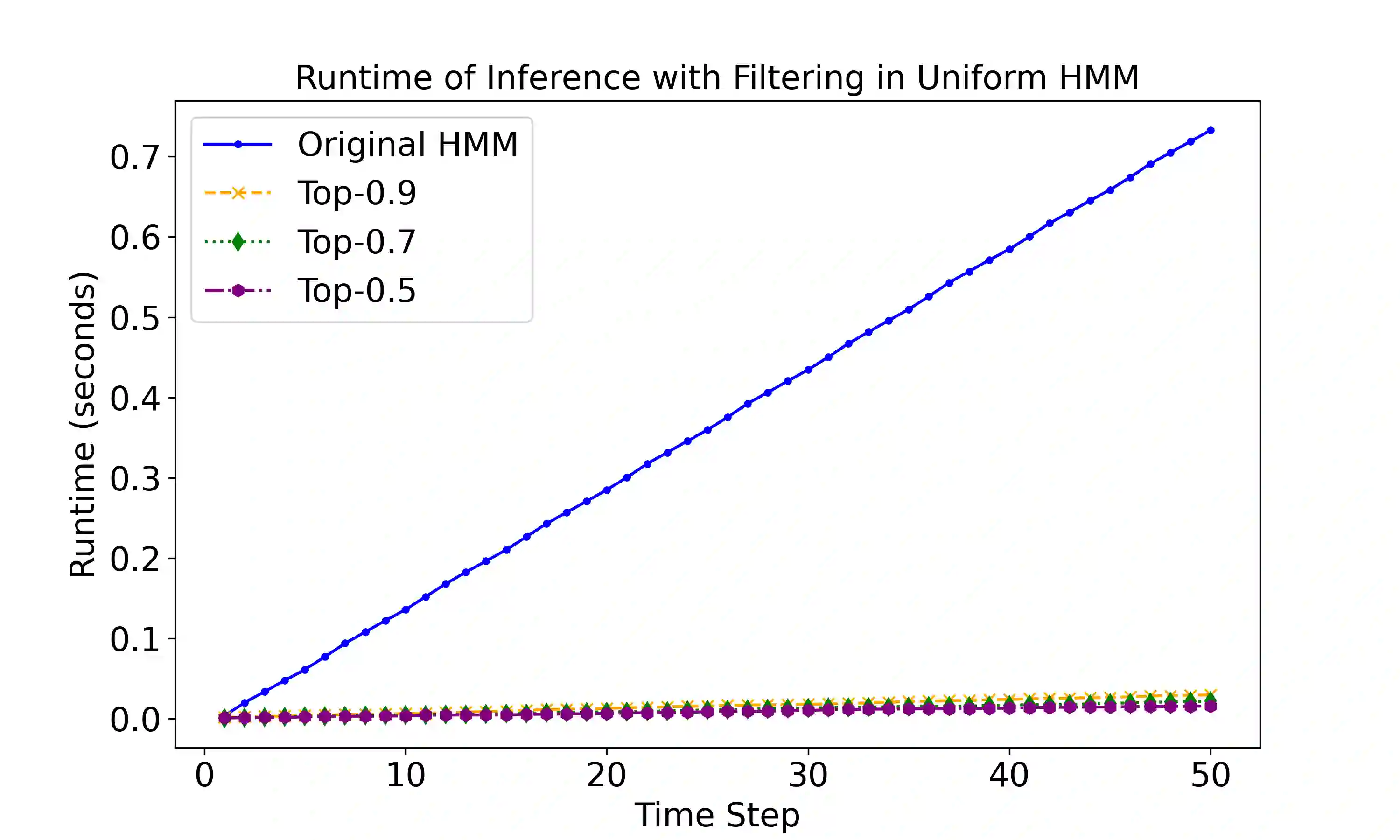
Inference in dynamic probabilistic models is a complex task involving expensive operations. In particular, for Hidden Markov Models, the whole state space has to be enumerated for advancing in time. Even states with negligible probabilities are considered, resulting in computational inefficiency and increased noise due to the propagation of unlikely probability mass. We propose to denoise the future and speed up inference by using only the top-p states, i.e., the most probable states with accumulated probability p. We show that the error introduced by using only the top-p states is bound by p and the so-called minimal mixing rate of the underlying model. Moreover, in our empirical evaluation, we show that we can expect speedups of at least an order of magnitude, while the error in terms of total variation distance is below 0.09.

翻译：动态概率模型中的推理是一项涉及昂贵运算的复杂任务。特别地，对于隐马尔可夫模型，时间推进需要对整个状态空间进行枚举。即使概率可忽略的状态也被纳入计算，这导致计算效率低下，且由于低概率质量的传播而引入额外噪声。我们提出通过仅使用top-p状态（即累积概率为p的最可能状态）来对"未来"进行去噪并加速推理。我们证明，仅使用top-p状态引入的误差受p值和模型最小混合率的共同约束。此外，在实证评估中，我们证明该方法可预期获得至少一个数量级的加速效果，同时总变差距离误差低于0.09。