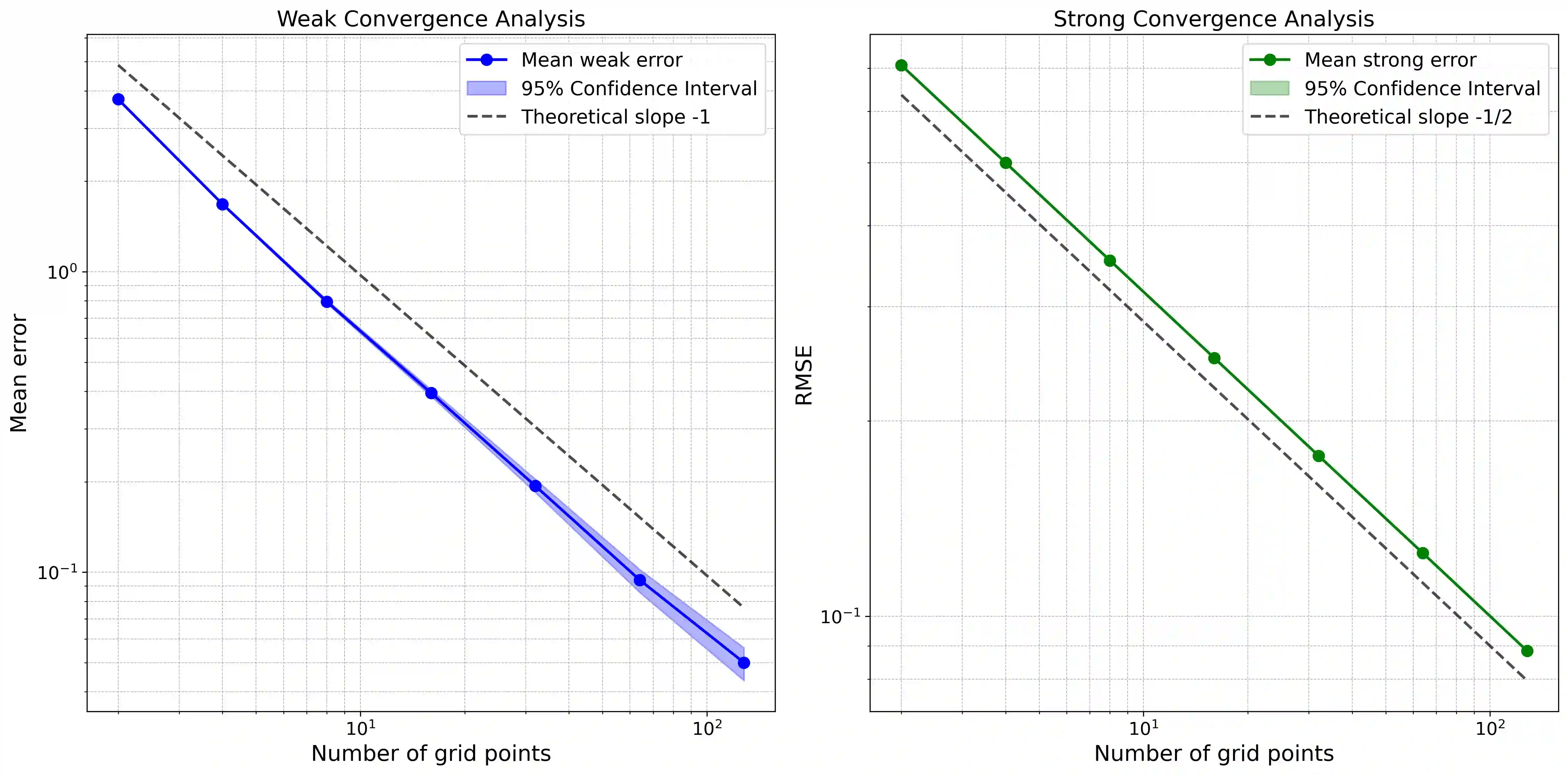
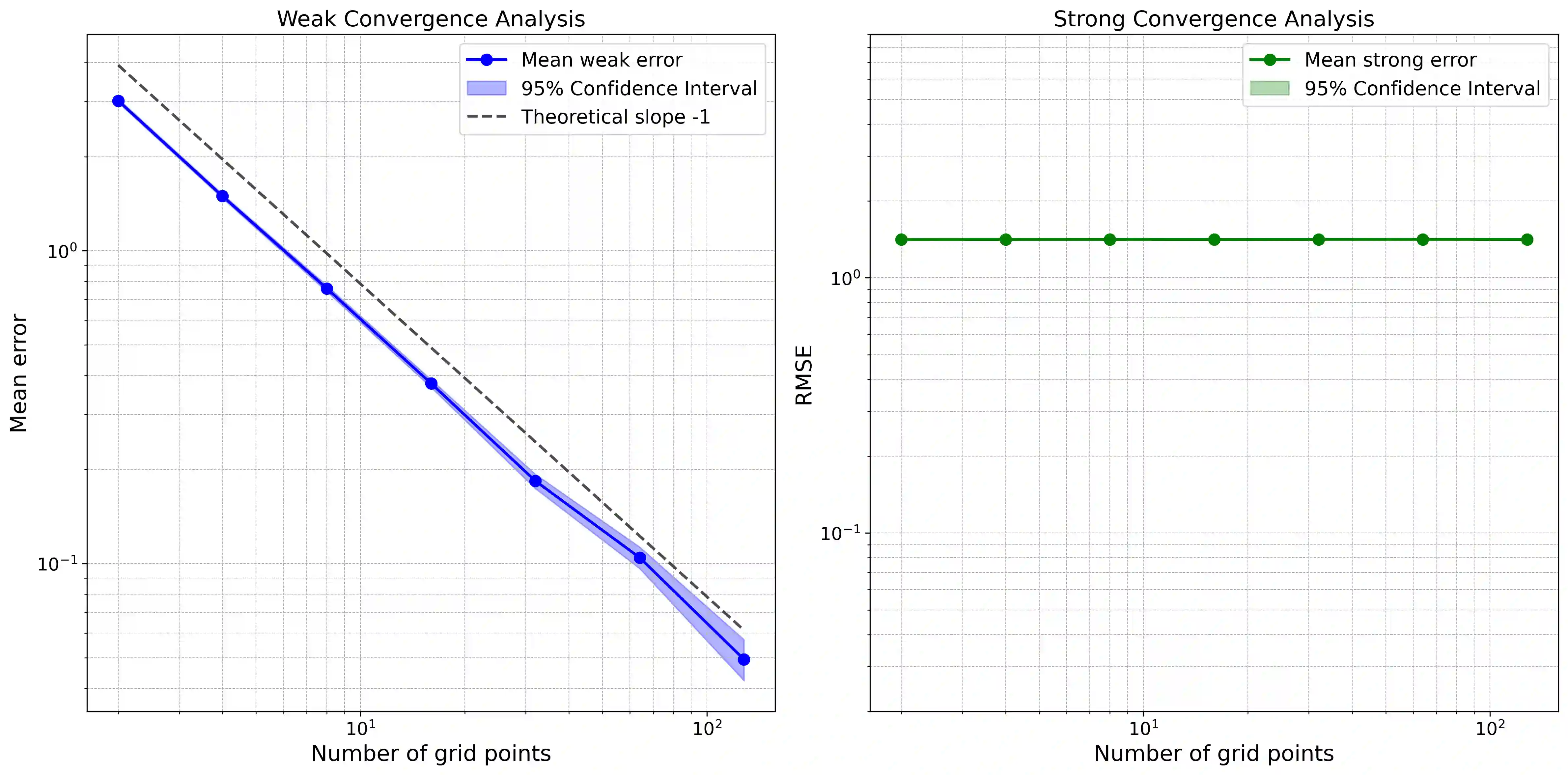
Stochastic policies (also known as relaxed controls) are widely used in continuous-time reinforcement learning algorithms. However, executing a stochastic policy and evaluating its performance in a continuous-time environment remain open challenges. This work introduces and rigorously analyzes a policy execution framework that samples actions from a stochastic policy at discrete time points and implements them as piecewise constant controls. We prove that as the sampling mesh size tends to zero, the controlled state process converges weakly to the dynamics with coefficients aggregated according to the stochastic policy. We explicitly quantify the convergence rate based on the regularity of the coefficients and establish an optimal first-order convergence rate for sufficiently regular coefficients. Additionally, we prove a $1/2$-order weak convergence rate that holds uniformly over the sampling noise with high probability, and establish a $1/2$-order pathwise convergence for each realization of the system noise in the absence of volatility control. Building on these results, we analyze the bias and variance of various policy evaluation and policy gradient estimators based on discrete-time observations. Our results provide theoretical justification for the exploratory stochastic control framework in [H. Wang, T. Zariphopoulou, and X.Y. Zhou, J. Mach. Learn. Res., 21 (2020), pp. 1-34].

翻译：随机策略（亦称松弛控制）在连续时间强化学习算法中广泛应用。然而，在连续时间环境中执行随机策略并评估其性能仍是待解决的挑战。本文提出并严格分析了一种策略执行框架，该框架在离散时间点从随机策略中采样动作，并将其实现为分段常数控制。我们证明，当采样网格尺寸趋于零时，受控状态过程弱收敛于按随机策略聚合系数后的动态系统。我们基于系数的正则性明确量化了收敛速率，并对充分正则的系数建立了最优的一阶收敛速率。此外，我们证明了以高概率在采样噪声上一致成立的 $1/2$ 阶弱收敛速率，并在无波动率控制的情况下，为系统噪声的每个实现建立了 $1/2$ 阶路径收敛。基于这些结果，我们分析了基于离散时间观测的各种策略评估与策略梯度估计器的偏差与方差。我们的结果为[H. Wang, T. Zariphopoulou, and X.Y. Zhou, J. Mach. Learn. Res., 21 (2020), pp. 1-34]中的探索性随机控制框架提供了理论依据。