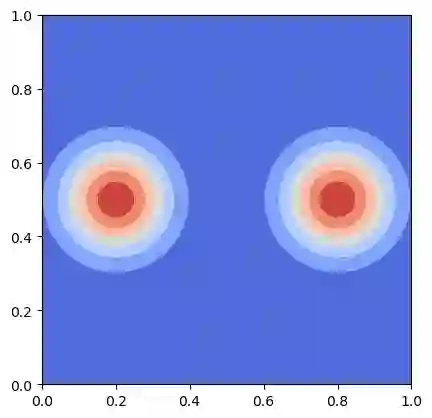
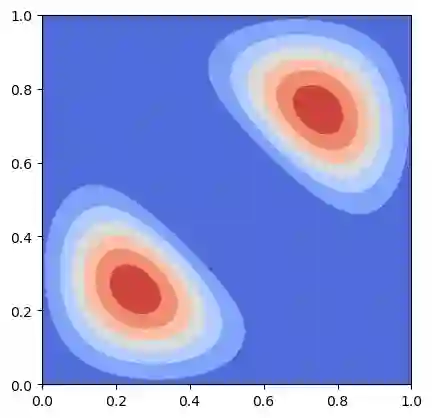
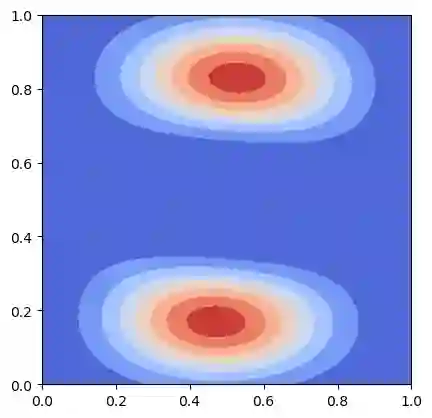
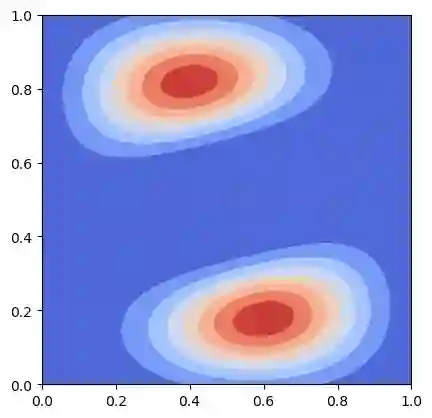
We propose a MFG model with quadratic Hamiltonian involving $N$ populations. This results in a system of $N$ Hamilton-Jacobi-Bellman and $N$ Fokker-Planck equations with non-local interactions. As in the classical case we introduce an Eulerian variational formulation which, despite the non convexity of the interaction, still gives a weak solution to the MFG model. The problem can be reformulated in Lagrangian terms and solved numerically by a Sinkhorn-like scheme. We present numerical results based on this approach, these simulations exhibit different behaviours depending on the nature (repulsive or attractive) of the non-local interaction.

翻译：我们提出了一种包含N个群体的平均场博弈模型，其哈密顿量为二次型。该模型导出了一个具有非局部相互作用的N个哈密顿-雅可比-贝尔曼方程和N个福克-普朗克方程组成的系统。与经典情形类似，我们引入了欧拉变分公式，尽管相互作用具有非凸性，该公式仍能为平均场博弈模型提供弱解。该问题可重新表述为拉格朗日形式，并通过类Sinkhorn算法进行数值求解。我们展示了基于此方法的数值结果，这些模拟根据非局部相互作用的性质（排斥性或吸引性）呈现出不同的行为模式。