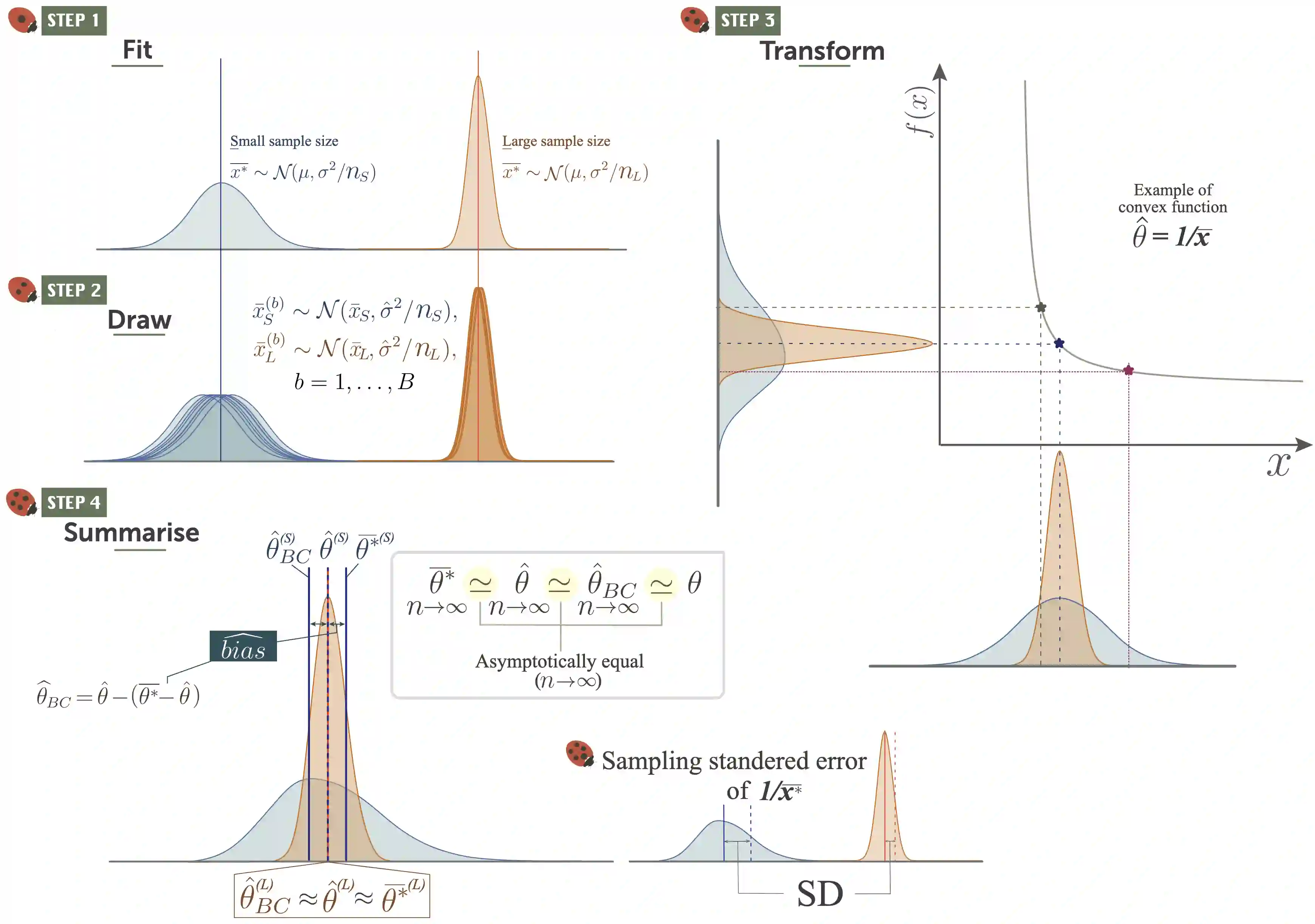
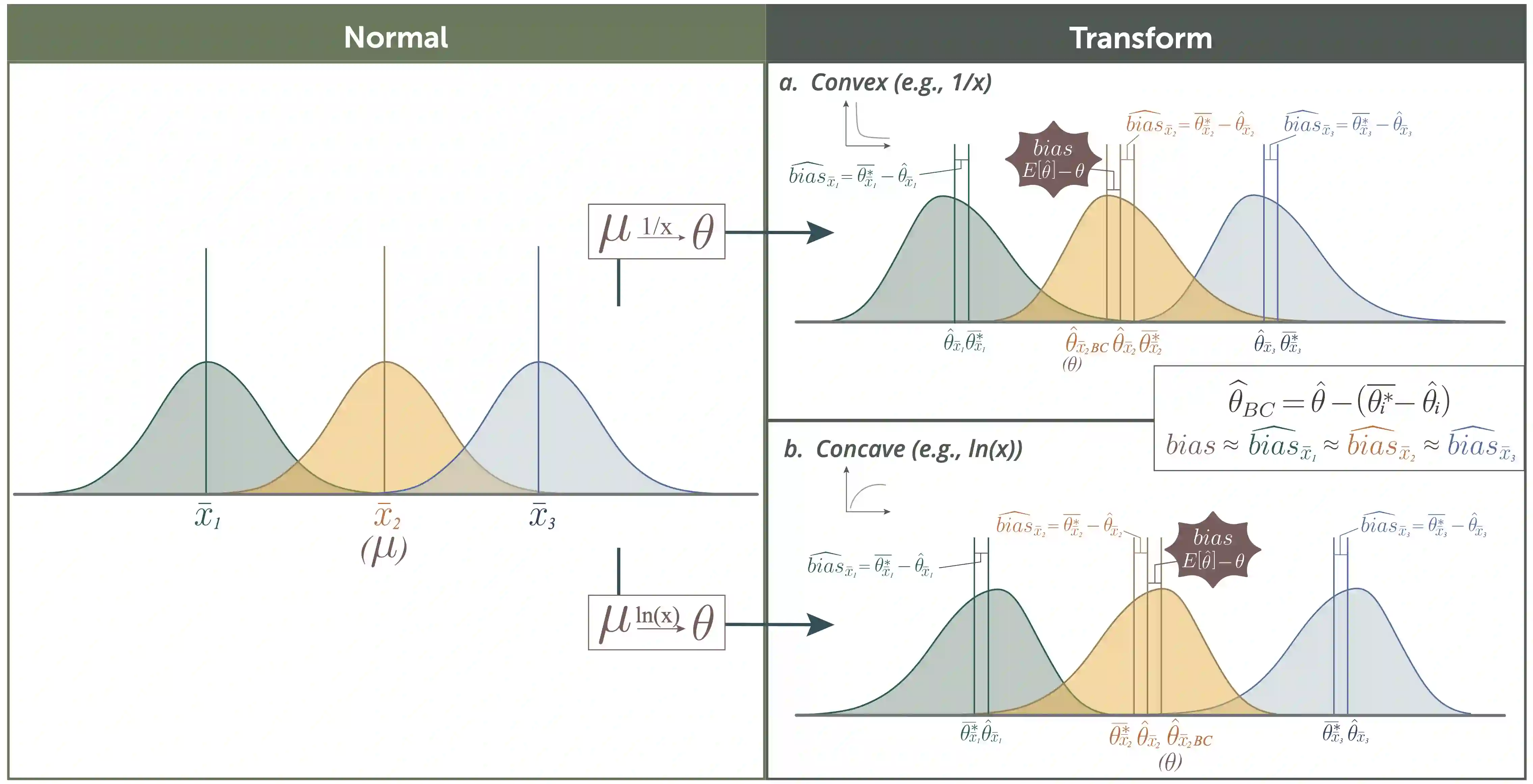
Meta-analyses require an effect-size estimate and its corresponding sampling variance from primary studies. In some cases, estimators for the sampling variance of a given effect size statistic may not exist, necessitating the derivation of a new formula for sampling variance. Traditionally, sampling variance formulas are obtained via hand-derived Taylor expansions (the delta method), though this procedure can be challenging for non-statisticians. Building on the idea of single-fit parametric resampling, we introduce SAFE bootstrap: a Single-fit, Accurate, Fast, and Easy simulation recipe that replaces potentially complex algebra with four intuitive steps: fit, draw, transform, and summarise. In a unified framework, the SAFE bootstrap yields bias-corrected point estimates and standard errors for any effect size statistic, regardless of whether the outcome is continuous or discrete. SAFE bootstrapping works by drawing once from a simple sampling model (normal, binomial, etc.), converting each replicate into any effect size of interest and then calculating the bias and sampling variance from simulated data. We demonstrate how to implement the SAFE bootstrap for a simple example first, and then for common effect sizes, such as the standardised mean difference and log odds ratio, as well as for less common effect sizes. With some additional coding, SAFE can also handle zero values and small sample sizes. Our tutorial, with R code supplements, should not only enhance understanding of sampling variance for effect sizes, but also serve as an introduction to the power of simulation-based methods for deriving any effect size with bias correction and its associated sampling variance.

翻译：元分析需要从原始研究中获取效应量估计值及其对应的抽样方差。在某些情况下，特定效应量统计量的抽样方差估计器可能不存在，因此需要推导新的抽样方差公式。传统上，抽样方差公式通过手工推导的泰勒展开（Delta方法）获得，但这一过程对非统计学家而言可能具有挑战性。基于单次拟合参数重采样的思想，我们提出了SAFE自助法：一种单次拟合、准确、快速且易于操作的模拟方案，用四个直观步骤（拟合、抽取、转换、汇总）替代了可能复杂的代数推导。在统一框架下，SAFE自助法可为任意效应量统计量生成偏差校正的点估计和标准误，无论结果是连续型还是离散型。SAFE自助法通过从简单抽样模型（正态分布、二项分布等）中单次抽取数据，将每次重复转换为目标效应量，然后基于模拟数据计算偏差和抽样方差。我们首先通过一个简单示例演示如何实现SAFE自助法，随后将其应用于常见效应量（如标准化均值差和对数比值比）以及较不常见的效应量。通过额外编码，SAFE方法还能处理零值和小样本情况。本教程附有R代码补充材料，不仅有助于深化对效应量抽样方差的理解，还可作为基于模拟方法推导任意效应量（含偏差校正）及其抽样方差的入门指南。