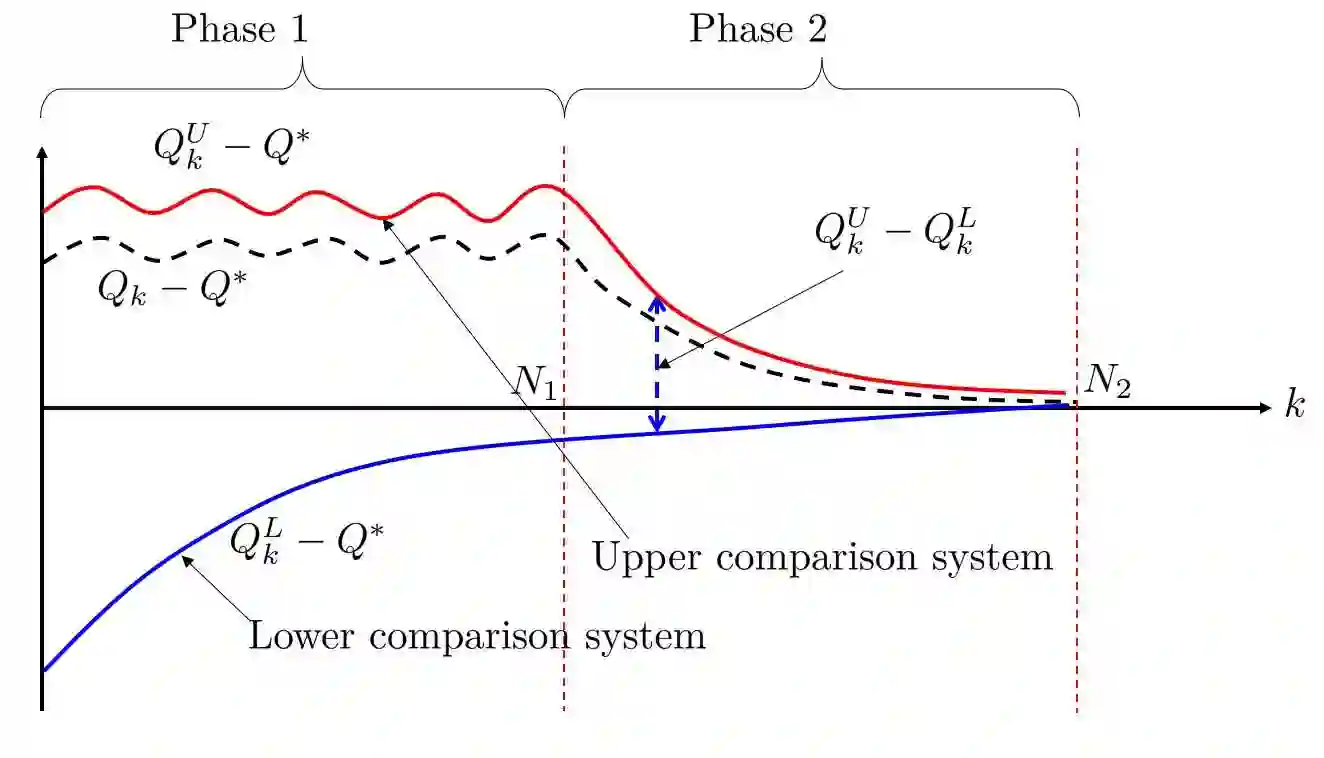
This paper develops a novel control-theoretic framework to analyze the non-asymptotic convergence of Q-learning. We show that the dynamics of asynchronous Q-learning with a constant step-size can be naturally formulated as a discrete-time stochastic affine switching system. Moreover, the evolution of the Q-learning estimation error is over- and underestimated by trajectories of two simpler dynamical systems. Based on these two systems, we derive a new finite-time error bound of asynchronous Q-learning when a constant stepsize is used. Our analysis also sheds light on the overestimation phenomenon of Q-learning. We further illustrate and validate the analysis through numerical simulations.

翻译：本文开发了一个新的控制理论框架, 用于分析Q- 学习的非同步融合。 我们显示, 具有恒定步尺寸的无同步Q学习的动态可以自然地被设计成一个离散时间切开的松动切片切换系统。 此外, Q- 学习估计错误的演变被两个更简单的动态系统的轨迹所过度和低估。 在这两个系统的基础上, 我们得出了一个新的有限时间错误, 在使用恒定步态时, 将不同步Q- 学习捆绑在一起。 我们的分析还揭示了Q- 学习的过高估计现象。 我们通过数字模拟进一步说明和验证分析。