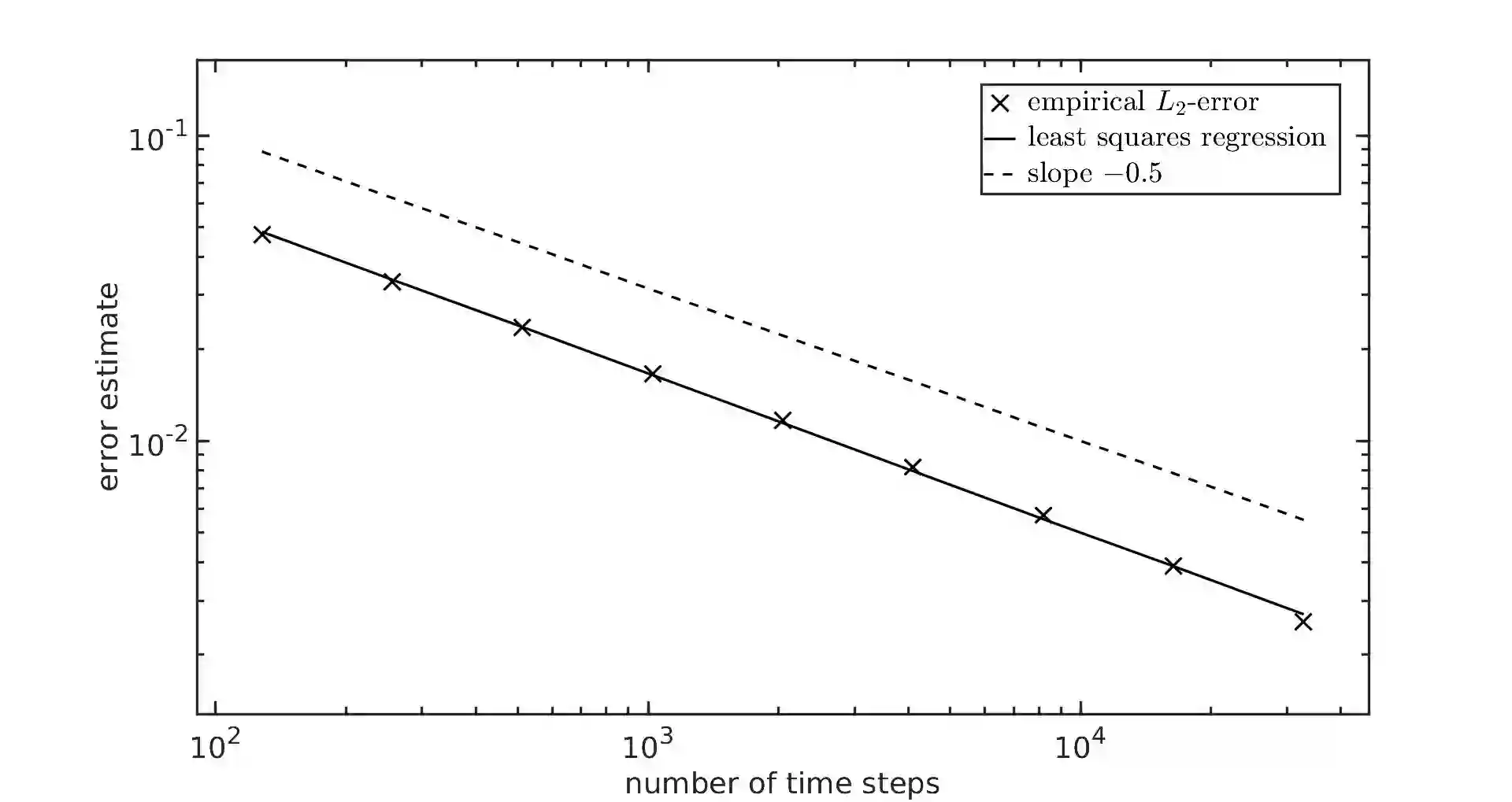
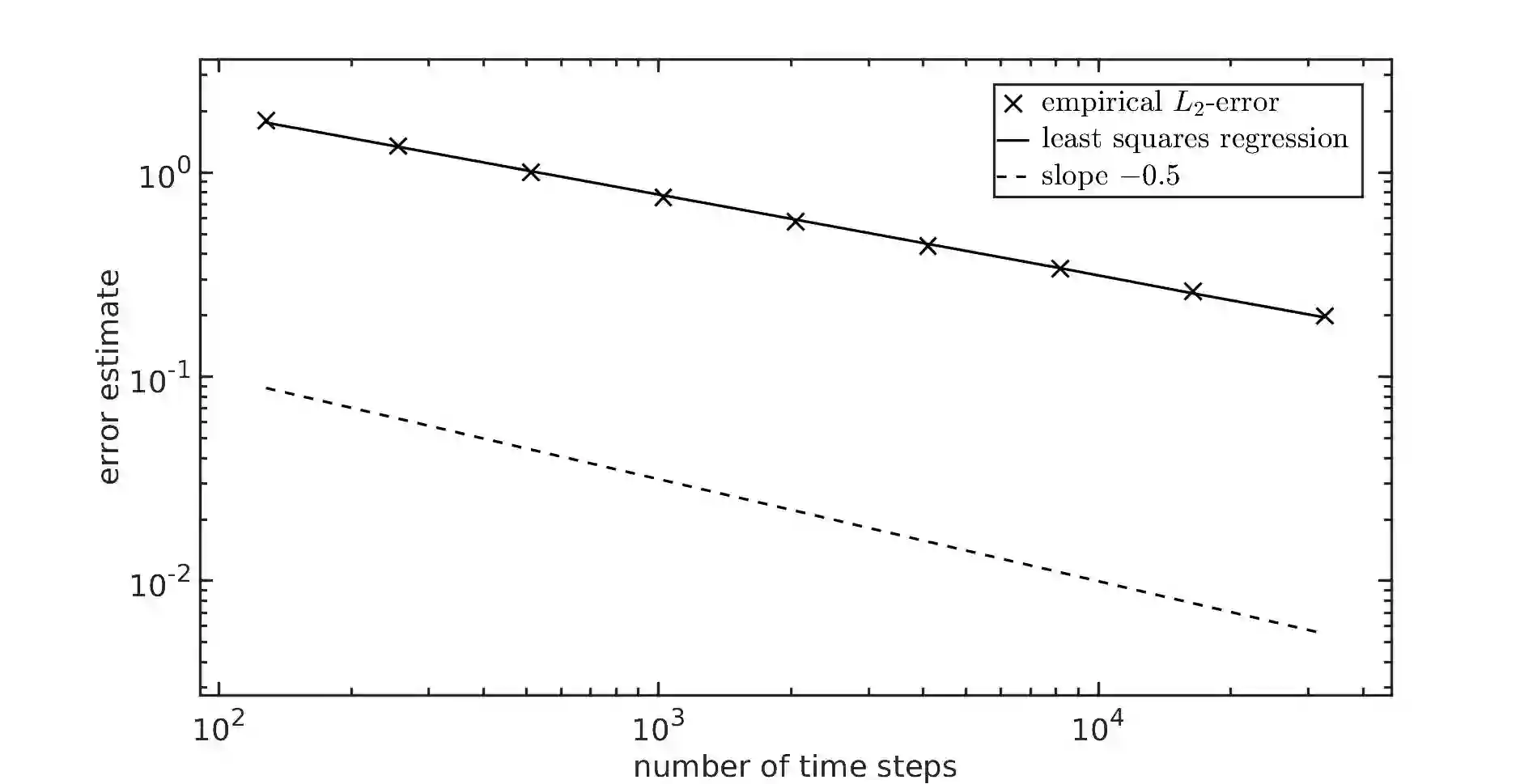
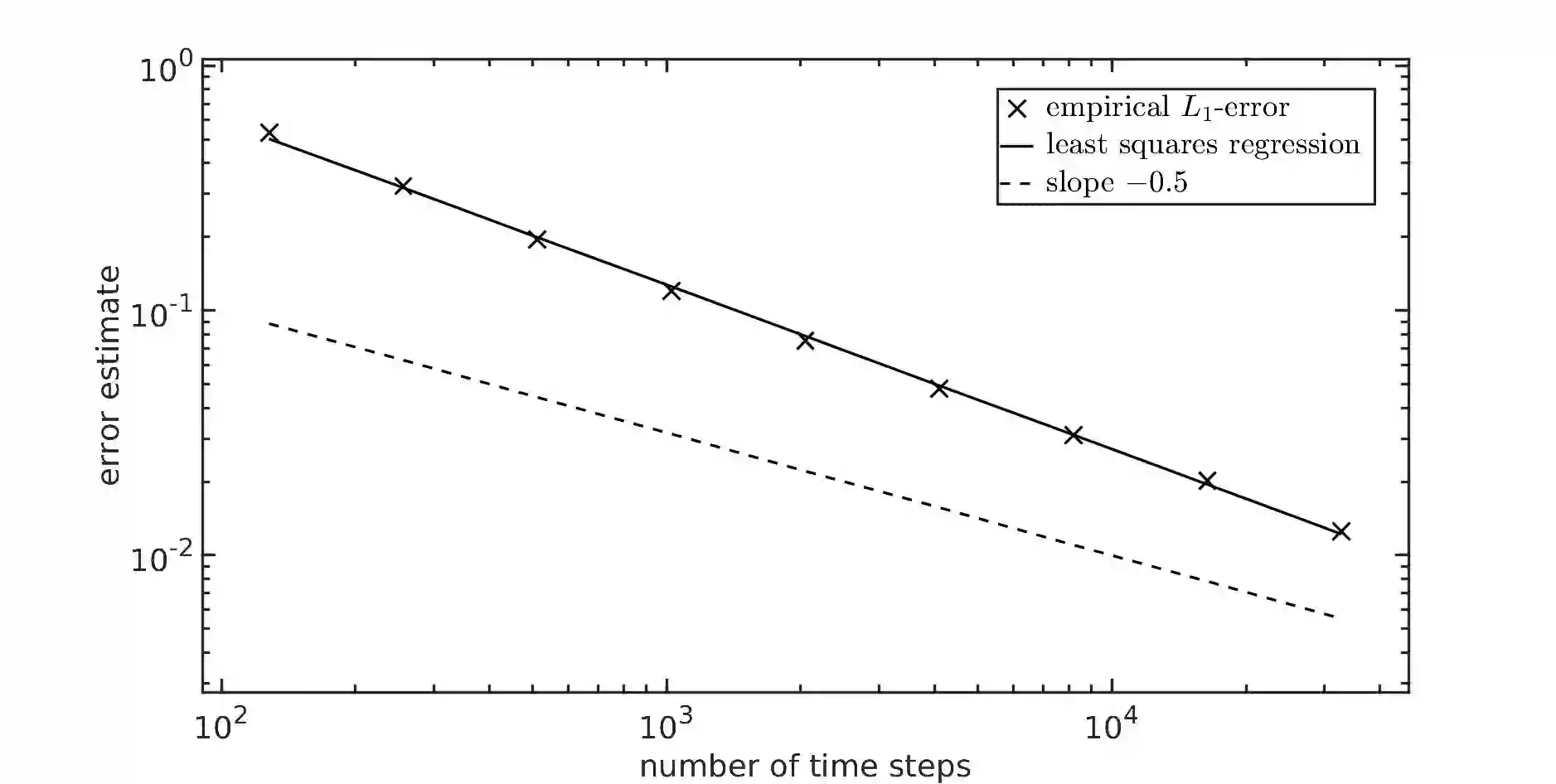
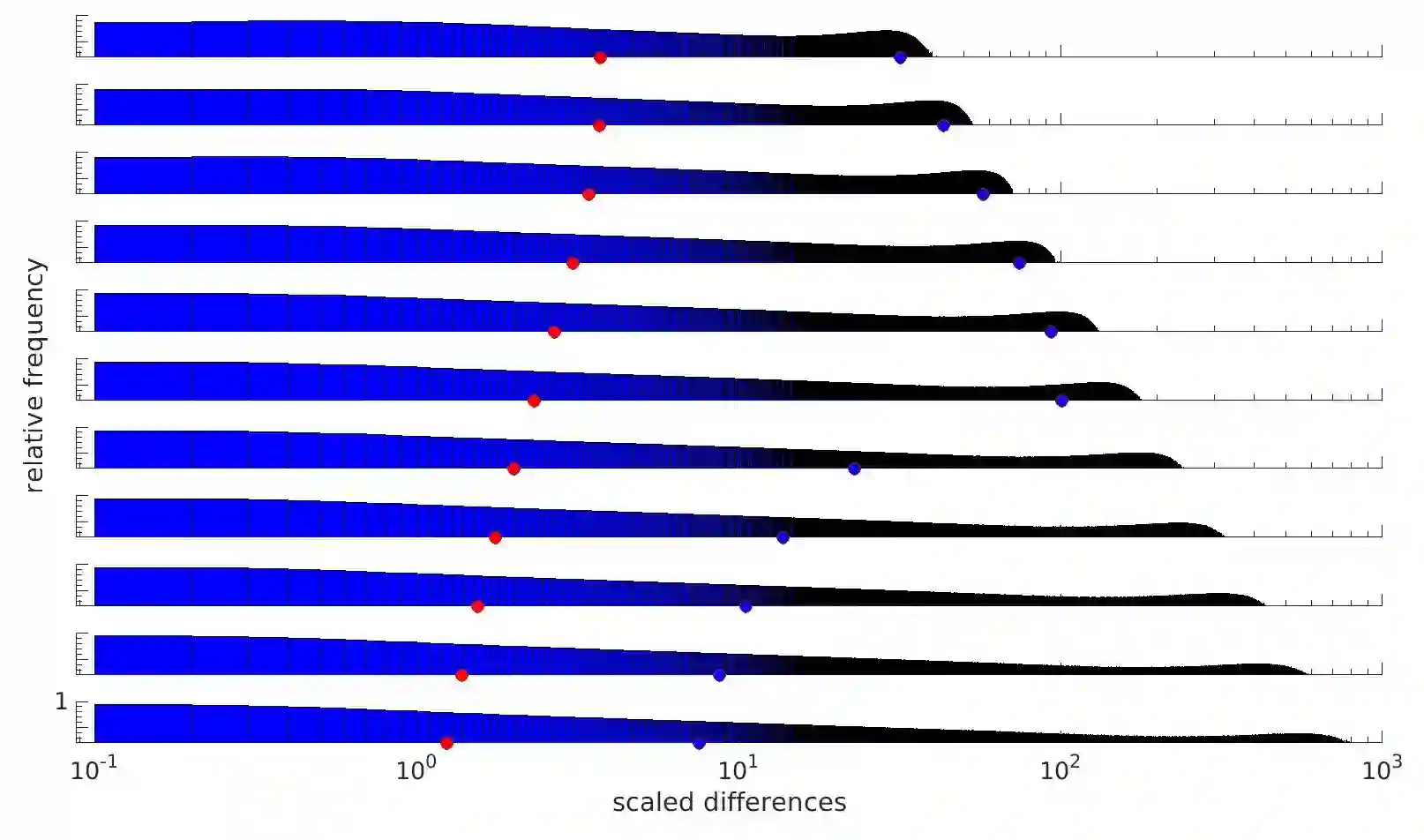
We study strong approximation of $d$-dimensional stochastic differential equations (SDEs) with a discontinuous drift coefficient. More precisely, we essentially assume that the drift coefficient is piecewise Lipschitz continuous with an exceptional set $\Theta\subset \mathbb{R}^d$ that is an orientable $C^4$-hypersurface of positive reach, the diffusion coefficient is assumed to be Lipschitz continuous and, in a neighborhood of $\Theta$, both coefficients are bounded and the diffusion coefficient has a non-degenerate portion orthogonal to $\Theta$. In recent years, a number of results have been proven in the literature for strong approximation of such SDEs and, in particular, the performance of the Euler-Maruyama scheme was studied. For $d=1$ and finite $\Theta$ it was shown that the Euler-Maruyama scheme achieves an $L_p$-error rate of at least $1/2$ for all $p\geq 1$ as in the classical case of Lipschitz continuous coefficients. For $d>1$, it was only known so far, that the Euler-Maruyama scheme achieves an $L_2$-error rate of at least $1/4-$ if, additionally, the coefficients $\mu$ and $\sigma$ are globally bounded. In this article, we prove that in the above setting the Euler-Maruyama scheme in fact achieves an $L_{p}$-error rate of at least $1/2-$ for all $d\in\mathbb{N}$ and all $p\geq 1$. The proof of this result is based on the well-known approach of transforming such an SDE into an SDE with globally Lipschitz continuous coefficients, a new It\^{o} formula for a class of functions which are not globally $C^2$ and a detailed analysis of the expected total time that the actual position of the time-continuous Euler-Maruyama scheme and its position at the preceding time point on the underlying grid are on 'different sides' of the hypersurface $\Theta$.

翻译：本文研究具有不连续漂移系数的$d$维随机微分方程（SDE）的强逼近问题。具体而言，我们本质上假设漂移系数是分段Lipschitz连续的，其例外集$\Theta\subset \mathbb{R}^d$是一个具有正到达距离的可定向$C^4$超曲面；扩散系数假设为Lipschitz连续，且在$\Theta$的邻域内，两个系数均有界，同时扩散系数存在垂直于$\Theta$的非退化分量。近年来，文献中已证明此类SDE强逼近的若干结果，特别是对Euler-Maruyama格式的性能进行了研究。对于$d=1$且$\Theta$有限的情形，研究表明Euler-Maruyama格式在所有$p\geq 1$下至少能达到$1/2$的$L_p$误差阶，这与经典Lipschitz连续系数情形一致。对于$d>1$的情形，此前仅知当系数$\mu$和$\sigma$全局有界时，Euler-Maruyama格式至少能达到$1/4-$的$L_2$误差阶。本文证明在上述设定下，Euler-Maruyama格式实际上对所有$d\in\mathbb{N}$和$p\geq 1$均至少能达到$1/2-$的$L_{p}$误差阶。该结果的证明基于将此类SDE转化为具有全局Lipschitz连续系数SDE的经典方法、针对非全局$C^2$函数类的新Itô公式，以及对时间连续Euler-Maruyama格式的实际位置与其在底层网格前一时间点位置处于超曲面$\Theta$"两侧"的期望总时间的精细分析。