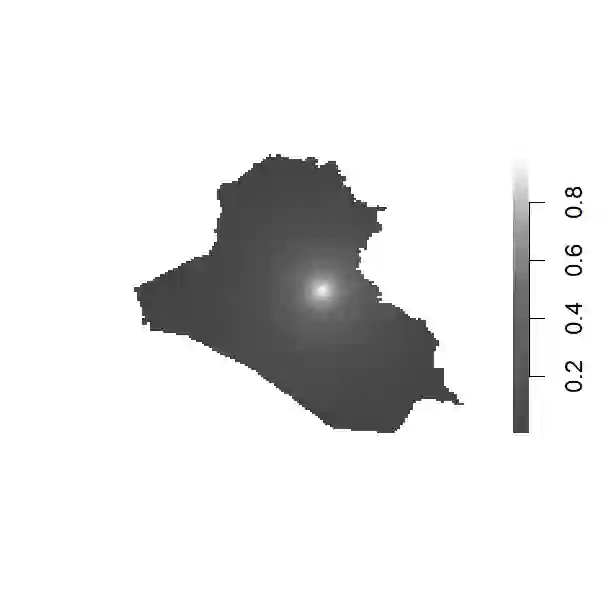
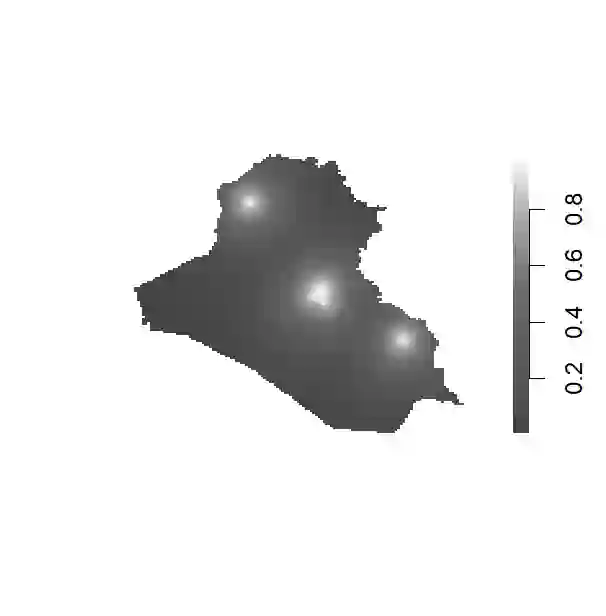
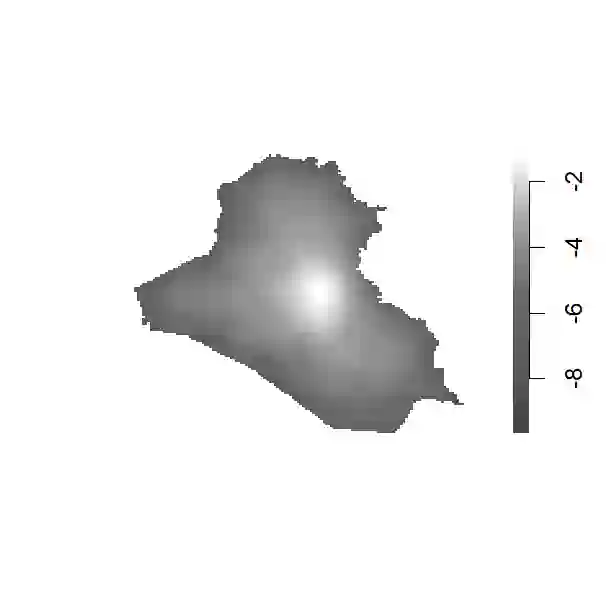
Scholars from diverse fields increasingly rely on high-frequency spatio-temporal data. Yet, causal inference with these data remains challenging due to spatial spillover and temporal carryover effects. We develop methods to estimate heterogeneous treatment effects by allowing for arbitrary spatial and temporal causal dependencies. We focus on common settings where the treatment and outcomes are time-varying spatial point patterns and where moderators are either spatial or spatio-temporal variables. We define causal estimands based on stochastic interventions where researchers specify counterfactual distributions of treatment events. We propose the Hajek-type estimator of the conditional average treatment effect (CATE) as a function of spatio-temporal moderator variables, and establish its asymptotic normality as the number of time periods increases. We then introduce a statistical test of no heterogeneous treatment effects. Through simulations, we evaluate the finite-sample performance of the proposed CATE estimator and its inferential properties. Our motivating application examines the heterogeneous effects of US airstrikes on insurgent violence in Iraq. Drawing on declassified spatio-temporal data, we examine how prior aid distributions moderate airstrike effects. Contrary to expectations from counterinsurgency theories, we find that prior aid distribution, along with greater amounts of aid per capita, is associated with increased insurgent attacks following airstrikes.

翻译：来自不同领域的学者日益依赖高频时空数据。然而，由于空间溢出效应和时间滞后效应，利用这些数据进行因果推断仍然具有挑战性。我们开发了通过允许任意空间和时间因果依赖性来估计异质性处理效应的方法。我们关注常见场景，其中处理和结果是时变的空间点模式，而调节变量是空间或时空变量。我们基于随机干预定义因果估计量，研究人员在此指定处理事件的反事实分布。我们提出了条件平均处理效应（CATE）作为时空调节变量函数的Hajek型估计量，并建立了其随着时间周期数增加而渐近正态的性质。随后，我们引入了无异质性处理效应的统计检验。通过模拟，我们评估了所提出的CATE估计量在有限样本下的性能及其推断特性。我们的激励性应用研究了美国空袭对伊拉克叛乱暴力的异质性影响。利用解密的时空数据，我们检验了先前援助分布如何调节空袭效果。与反叛乱理论的预期相反，我们发现先前的援助分布以及更高的人均援助金额与空袭后叛乱袭击的增加相关。