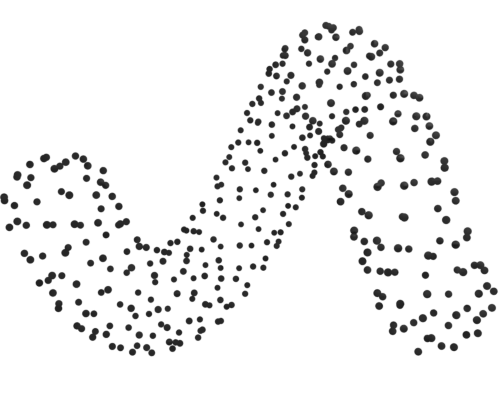Given a finite set of points $P$ sampling an unknown smooth surface $\mathcal{M} \subseteq \mathbb{R}^3$, our goal is to triangulate $\mathcal{M}$ based solely on $P$. Assuming $\mathcal{M}$ is a smooth orientable submanifold of codimension 1 in $\mathbb{R}^d$, we introduce a simple algorithm, Naive Squash, which simplifies the $\alpha$-complex of $P$ by repeatedly applying a new type of collapse called vertical relative to $\mathcal{M}$. Naive Squash also has a practical version that does not require knowledge of $\mathcal{M}$. We establish conditions under which both the naive and practical Squash algorithms output a triangulation of $\mathcal{M}$. We provide a bound on the angle formed by triangles in the $\alpha$-complex with $\mathcal{M}$, yielding sampling conditions on $P$ that are competitive with existing literature for smooth surfaces embedded in $\mathbb{R}^3$, while offering a more compartmentalized proof. As a by-product, we obtain that the restricted Delaunay complex of $P$ triangulates $\mathcal{M}$ when $\mathcal{M}$ is a smooth surface in $\mathbb{R}^3$ under weaker conditions than existing ones.

翻译：给定一个有限点集$P$，它采样了一个未知光滑曲面$\mathcal{M} \subseteq \mathbb{R}^3$，我们的目标仅基于$P$对$\mathcal{M}$进行三角剖分。假设$\mathcal{M}$是$\mathbb{R}^d$中一个光滑可定向的余维1子流形，我们引入了一种简单算法——朴素挤压算法，该算法通过反复应用一种相对于$\mathcal{M}$的新型坍缩（称为垂直坍缩）来简化$P$的$\alpha$复形。朴素挤压算法还有一个不需要知道$\mathcal{M}$的实用版本。我们建立了朴素和实用挤压算法输出$\mathcal{M}$三角剖分的条件。我们给出了$\alpha$复形中三角形与$\mathcal{M}$所成角度的界，从而得到了关于$P$的采样条件，这些条件对于嵌入$\mathbb{R}^3$的光滑曲面与现有文献相比具有竞争力，同时提供了一个更加模块化的证明。作为一个副产品，我们得到，当$\mathcal{M}$是$\mathbb{R}^3$中的光滑曲面时，在比现有条件更弱的条件下，$P$的限制Delaunay复形可以对$\mathcal{M}$进行三角剖分。