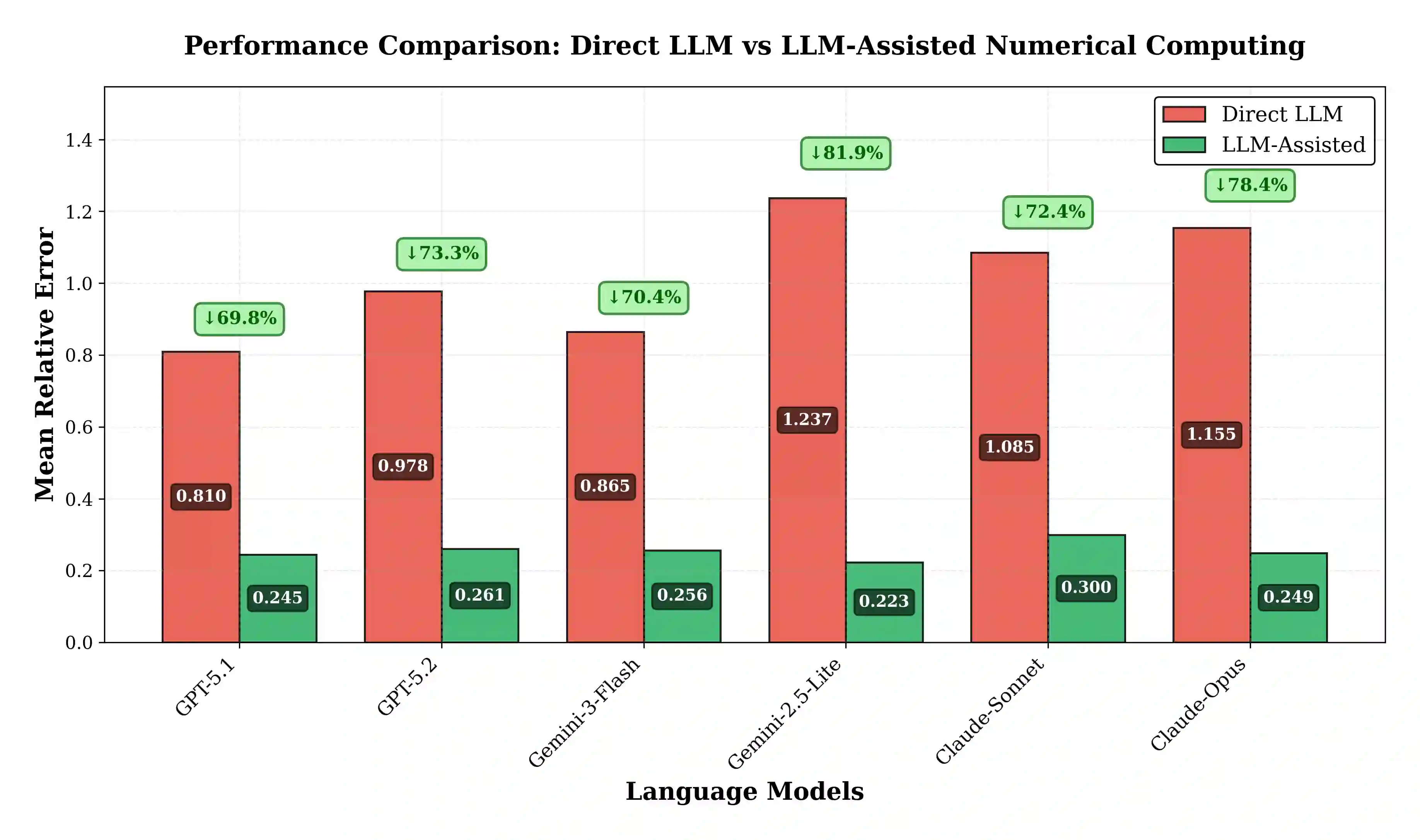
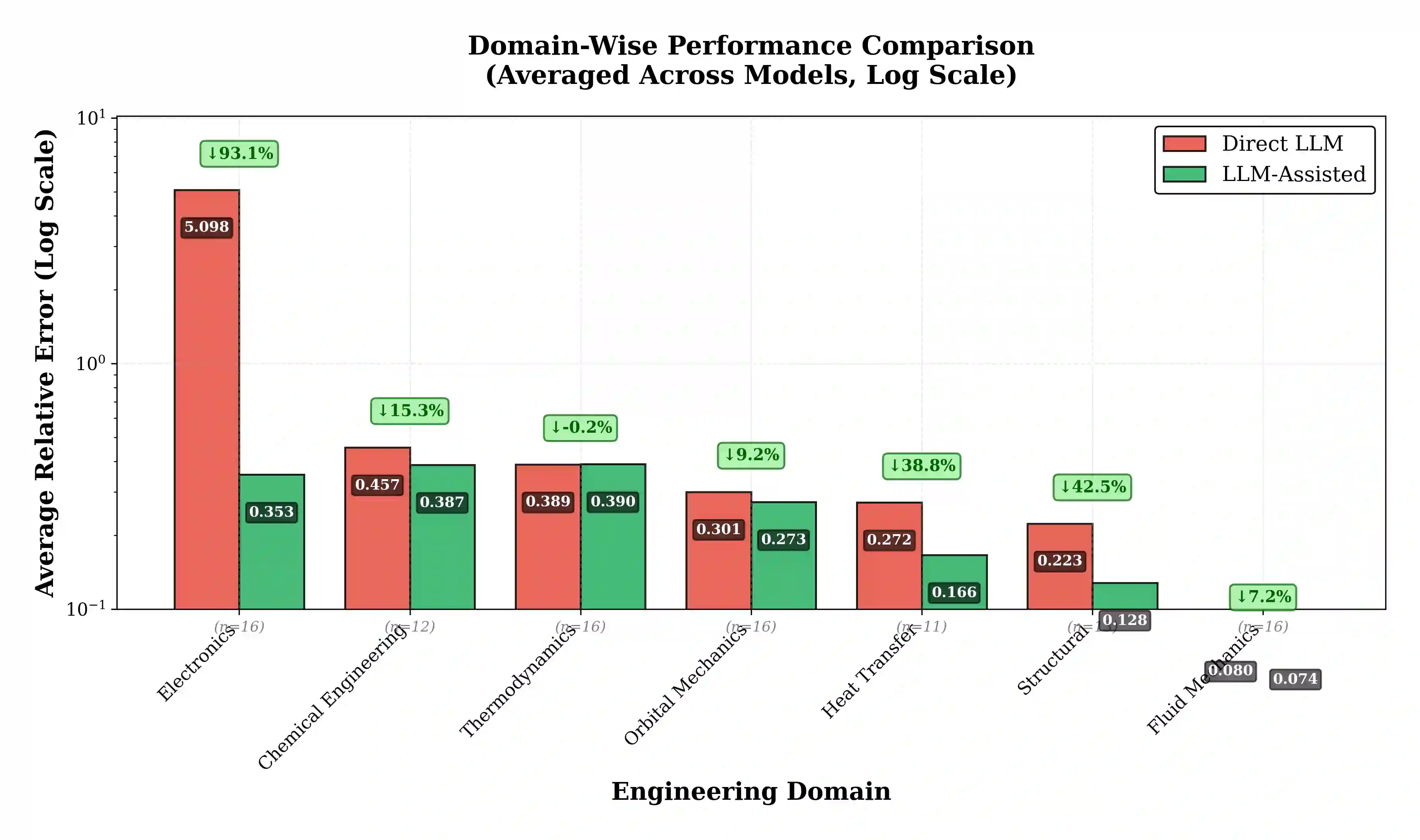
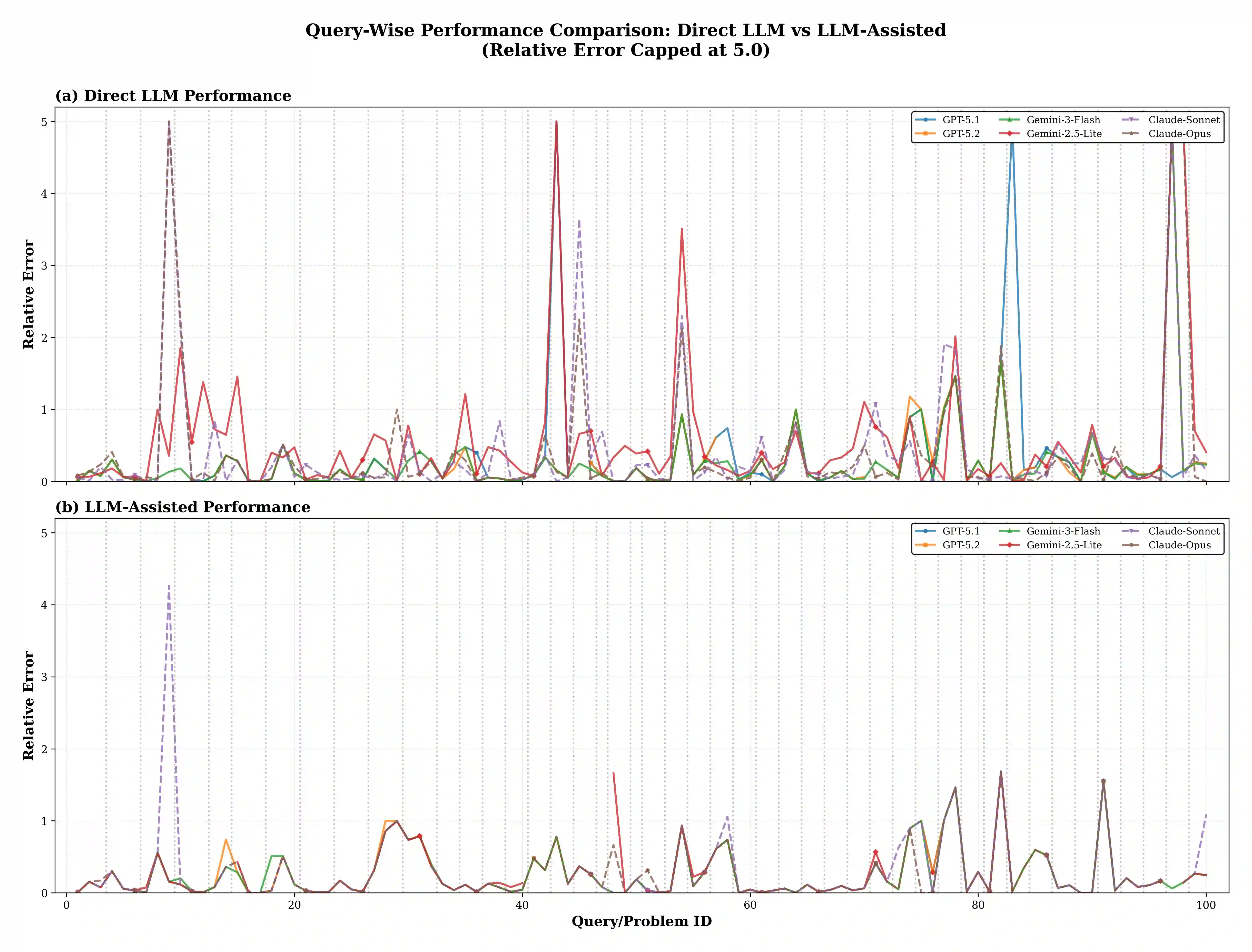
Transcendental equations requiring iterative numerical solution pervade engineering practice, from fluid mechanics friction factor calculations to orbital position determination. We systematically evaluate whether Large Language Models can solve these equations through direct numerical prediction or whether a hybrid architecture combining LLM symbolic manipulation with classical iterative solvers proves more effective. Testing six state-of-the-art models (GPT-5.1, GPT-5.2, Gemini-3-Flash, Gemini-2.5-Lite, Claude-Sonnet-4.5, Claude-Opus-4.5) on 100 problems spanning seven engineering domains, we compare direct prediction against solver-assisted computation where LLMs formulate governing equations and provide initial conditions while Newton-Raphson iteration performs numerical solution. Direct prediction yields mean relative errors of 0.765 to 1.262 across models, while solver-assisted computation achieves 0.225 to 0.301, representing error reductions of 67.9% to 81.8%. Domain-specific analysis reveals dramatic improvements in Electronics (93.1%) due to exponential equation sensitivity, contrasted with modest gains in Fluid Mechanics (7.2%) where LLMs exhibit effective pattern recognition. These findings establish that contemporary LLMs excel at symbolic manipulation and domain knowledge retrieval but struggle with precision-critical iterative arithmetic, suggesting their optimal deployment as intelligent interfaces to classical numerical solvers rather than standalone computational engines.

翻译：在工程实践中，从流体力学摩擦系数计算到轨道位置确定，普遍存在需要迭代数值求解的超越方程。我们系统评估了大型语言模型能否通过直接数值预测求解此类方程，以及将LLM符号操作与经典迭代求解器相结合的混合架构是否更为有效。在涵盖七个工程领域的100个问题上测试了六种前沿模型（GPT-5.1、GPT-5.2、Gemini-3-Flash、Gemini-2.5-Lite、Claude-Sonnet-4.5、Claude-Opus-4.5），比较了直接预测与求解器辅助计算两种方法：后者由LLM构建控制方程并提供初始条件，而由牛顿-拉弗森迭代执行数值求解。直接预测在各模型中的平均相对误差为0.765至1.262，而求解器辅助计算则达到0.225至0.301，误差降低了67.9%至81.8%。领域特异性分析显示，由于指数方程敏感性，电子学领域改进显著（93.1%）；而在流体力学领域，因LLM展现出有效的模式识别能力，改进相对有限（7.2%）。这些发现表明，当代LLM擅长符号操作和领域知识检索，但在精度要求严格的迭代算术运算方面存在局限，这提示其最佳部署方式是作为经典数值求解器的智能接口，而非独立的计算引擎。