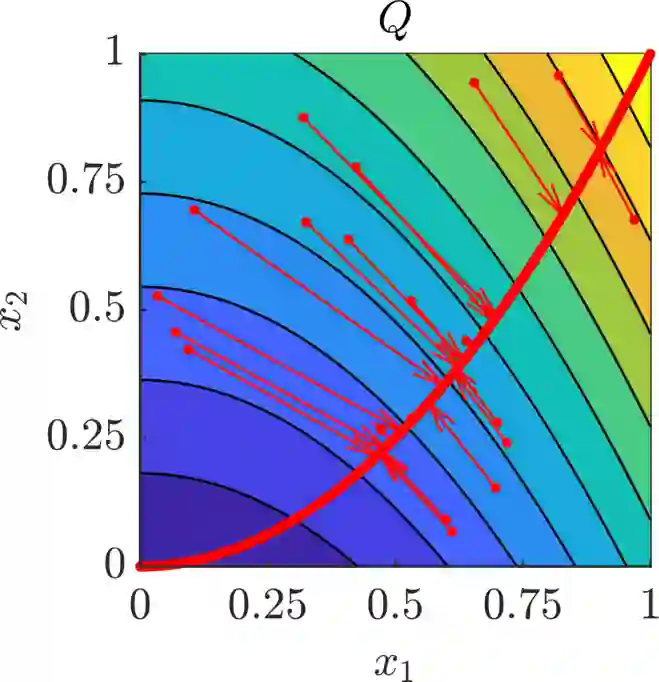
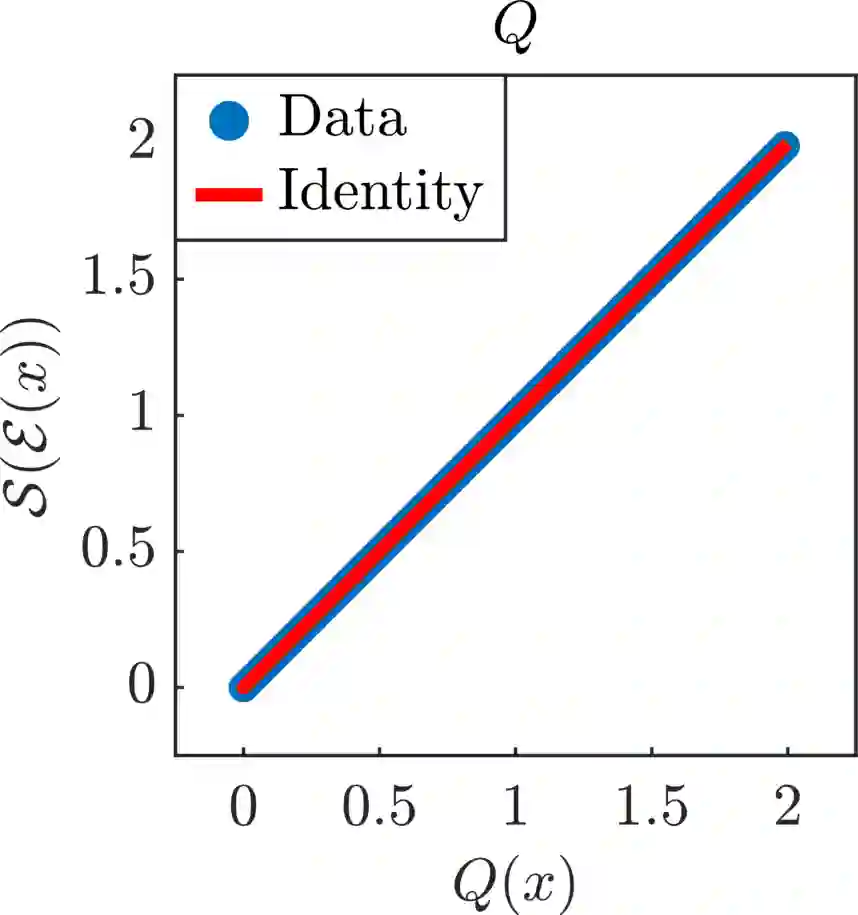
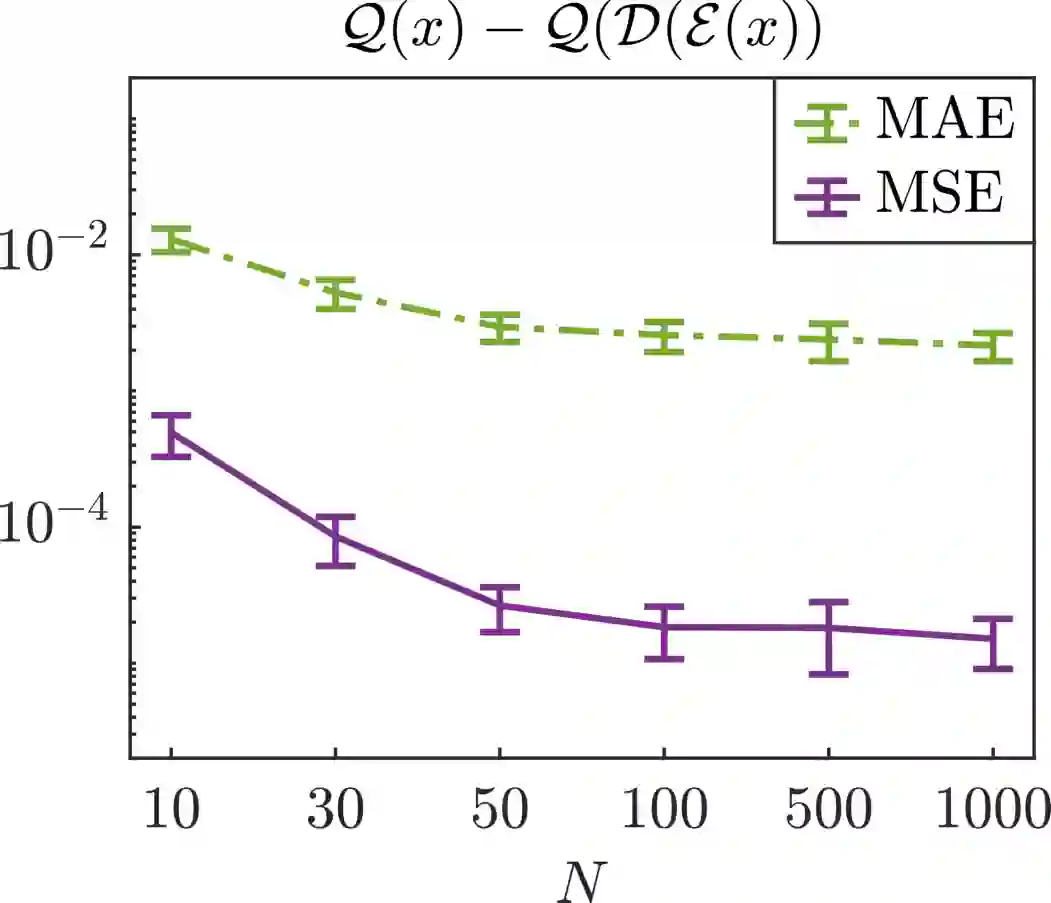
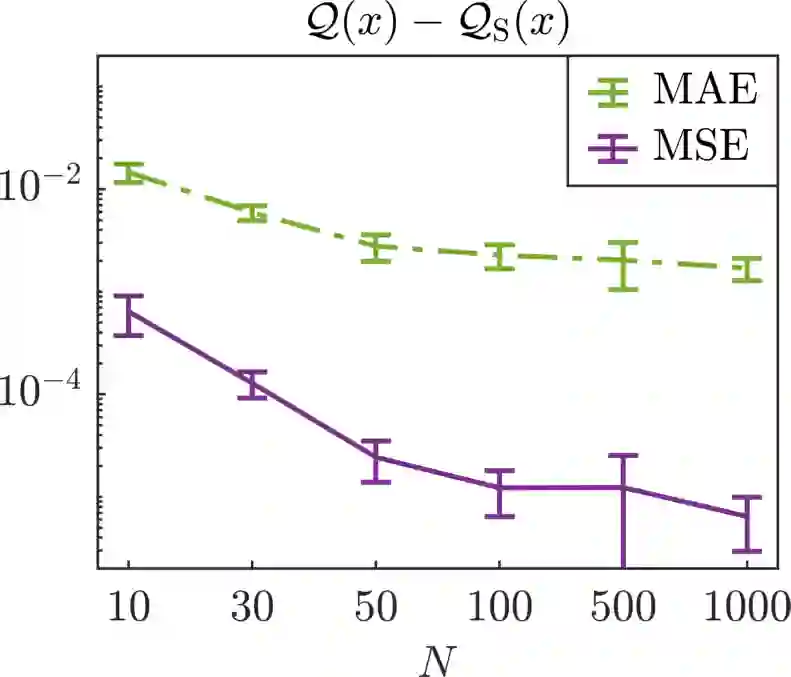
We present a new approach for nonlinear dimensionality reduction, specifically designed for computationally expensive mathematical models. We leverage autoencoders to discover a one-dimensional neural active manifold (NeurAM) capturing the model output variability, through the aid of a simultaneously learnt surrogate model with inputs on this manifold. Our method only relies on model evaluations and does not require the knowledge of gradients. The proposed dimensionality reduction framework can then be applied to assist outer loop many-query tasks in scientific computing, like sensitivity analysis and multifidelity uncertainty propagation. In particular, we prove, both theoretically under idealized conditions, and numerically in challenging test cases, how NeurAM can be used to obtain multifidelity sampling estimators with reduced variance by sampling the models on the discovered low-dimensional and shared manifold among models. Several numerical examples illustrate the main features of the proposed dimensionality reduction strategy and highlight its advantages with respect to existing approaches in the literature.

翻译：本文提出了一种新的非线性降维方法，专门针对计算成本高昂的数学模型。我们利用自编码器发现一个一维神经主动流形（NeurAM），该流形通过同时学习一个输入位于该流形上的代理模型来捕捉模型输出的变异性。我们的方法仅依赖于模型评估，无需梯度信息。所提出的降维框架可进一步应用于辅助科学计算中的外循环多查询任务，如敏感性分析和多保真度不确定性传播。特别地，我们从理论（在理想化条件下）和数值（在具有挑战性的测试案例中）两方面证明了如何利用NeurAM，通过在模型间共享的低维流形上进行采样，获得方差缩减的多保真度采样估计器。多个数值算例展示了所提降维策略的主要特性，并突显了其相对于现有文献方法的优势。