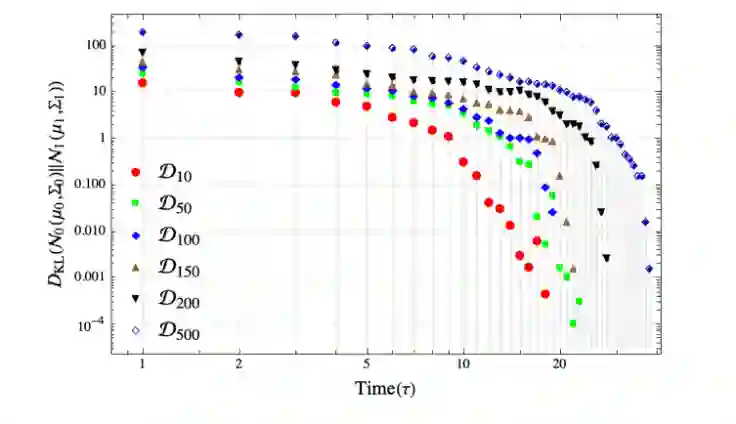
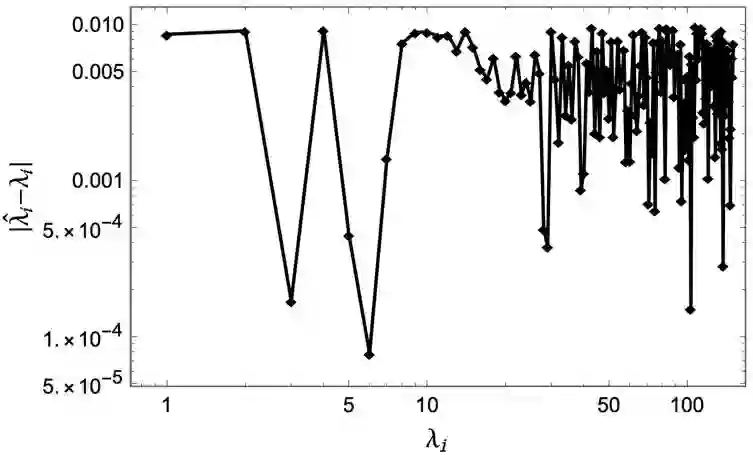
Despite the many challenges in exploratory data analysis, artificial neural networks have motivated strong interests in scientists and researchers both in theoretical as well as practical applications. Among sources of such popularity of artificial neural networks the ability of modeling non-linear dynamical systems, generalization, and adaptation possibilities should be mentioned. Despite this, there is still significant debate about the role of various underlying stochastic processes in stabilizing a unique structure for data learning and prediction. One of such obstacles to the theoretical and numerical study of machine intelligent systems is the curse of dimensionality and the sampling from high-dimensional probability distributions. In general, this curse prevents efficient description of states, providing a significant complexity barrier for the system to be efficiently described and studied. In this strand of research, direct treatment and description of such abstract notions of learning theory in terms of quantum information be one of the most favorable candidates. Hence, the subject matter of these articles is devoted to problems of design, adaptation and the formulations of computationally hard problems in terms of quantum mechanical systems. In order to characterize the microscopic description of such dynamics in the language of inferential statistics, covariance matrix estimation of d-dimensional Gaussian densities and Bayesian interpretation of eigenvalue problem for dynamical systems is assessed.

翻译：尽管探索性数据分析面临诸多挑战，人工神经网络仍在理论和实际应用层面激发了科学家与研究者的浓厚兴趣。人工神经网络之所以广受欢迎，应归功于其建模非线性动力系统的能力、泛化性以及适应可能性。尽管如此，关于各种基础随机过程在稳定数据学习与预测的独特结构中的作用仍存在显著争议。对机器智能系统进行理论与数值研究的障碍之一，是维度灾难以及从高维概率分布中采样的问题。一般而言，这种维度灾难阻碍了对状态的有效描述，为系统的高效描述与研究带来了显著的复杂性壁垒。在这一研究脉络中，用量子信息术语直接处理与描述学习理论的此类抽象概念，被视为最具前景的候选方向之一。因此，本文的研究主题致力于用量子力学系统来表述计算难题的设计、适应与形式化问题。为了用推断统计学的语言刻画此类动力学的微观描述，本文评估了d维高斯密度协方差矩阵的估计方法，以及动力系统特征值问题的贝叶斯解释。