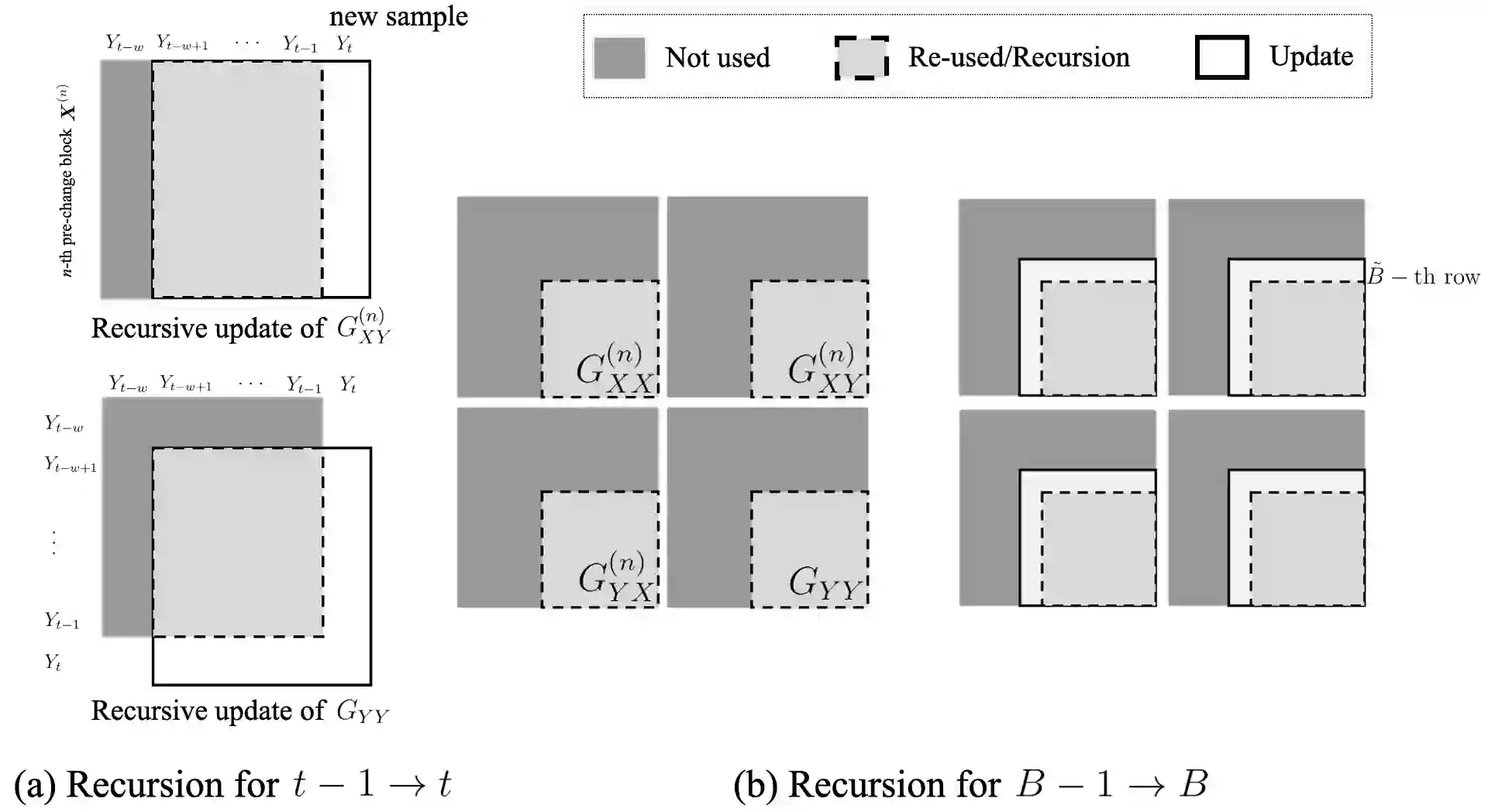
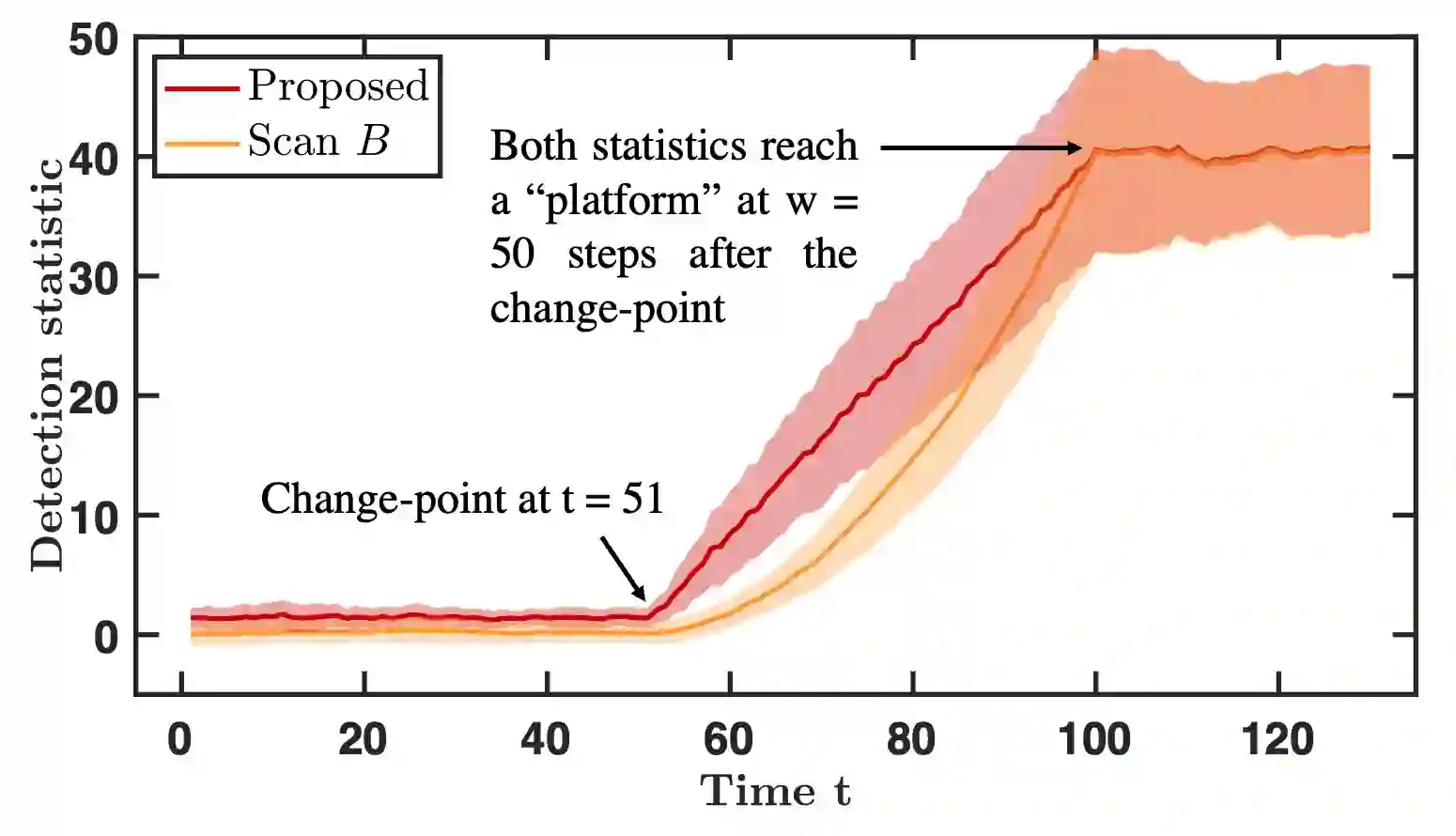
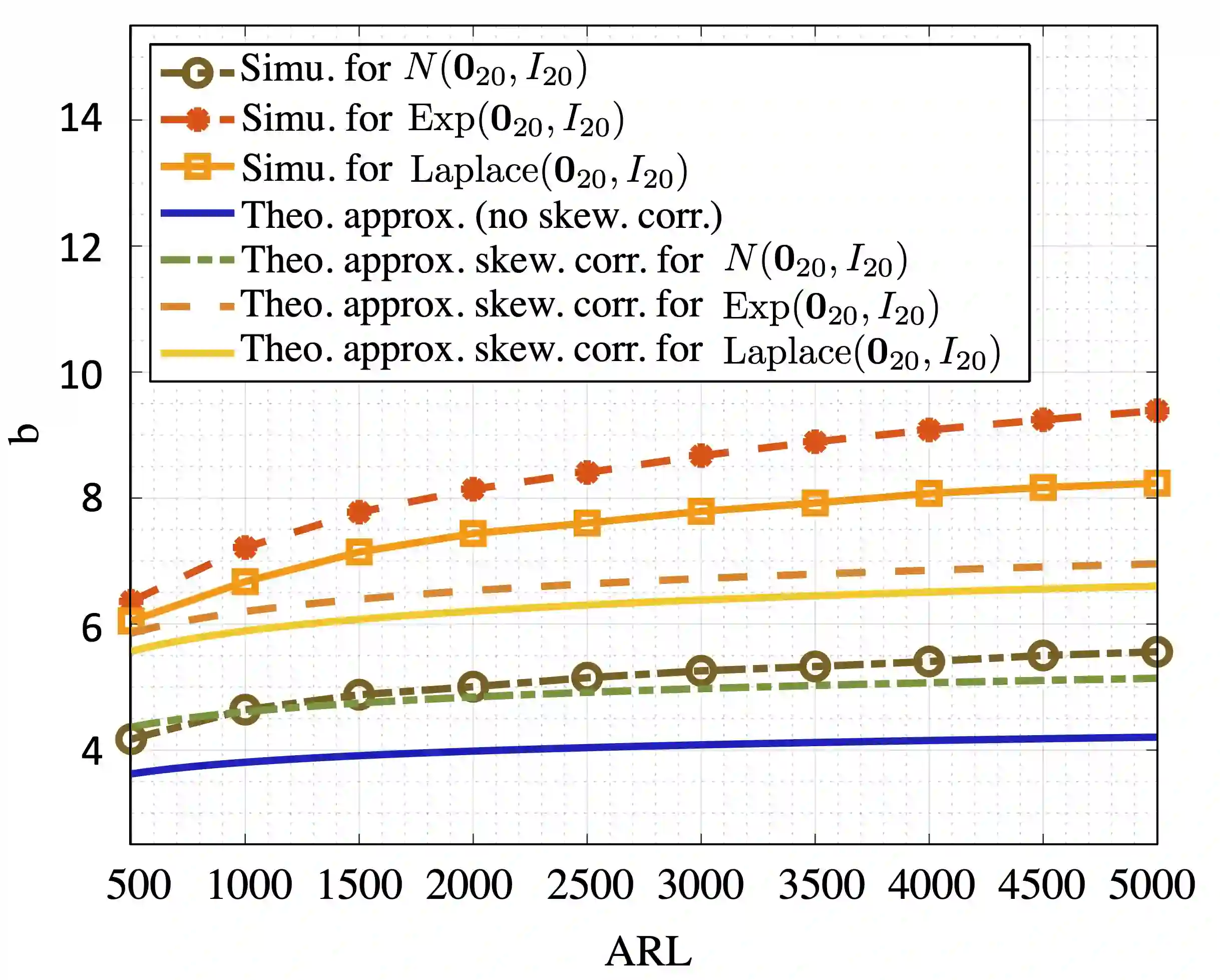
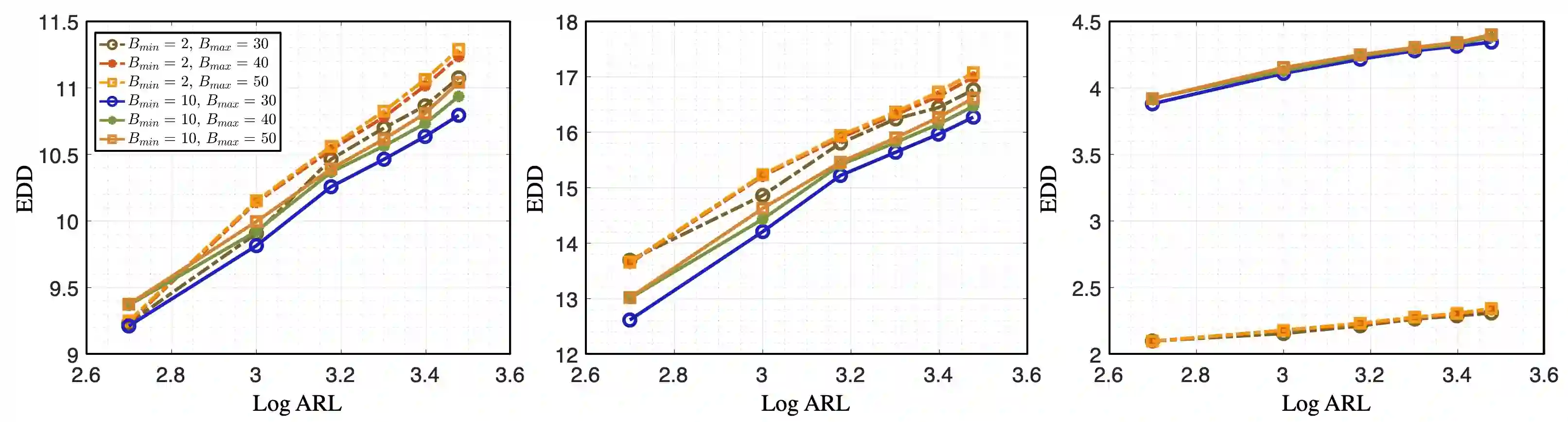
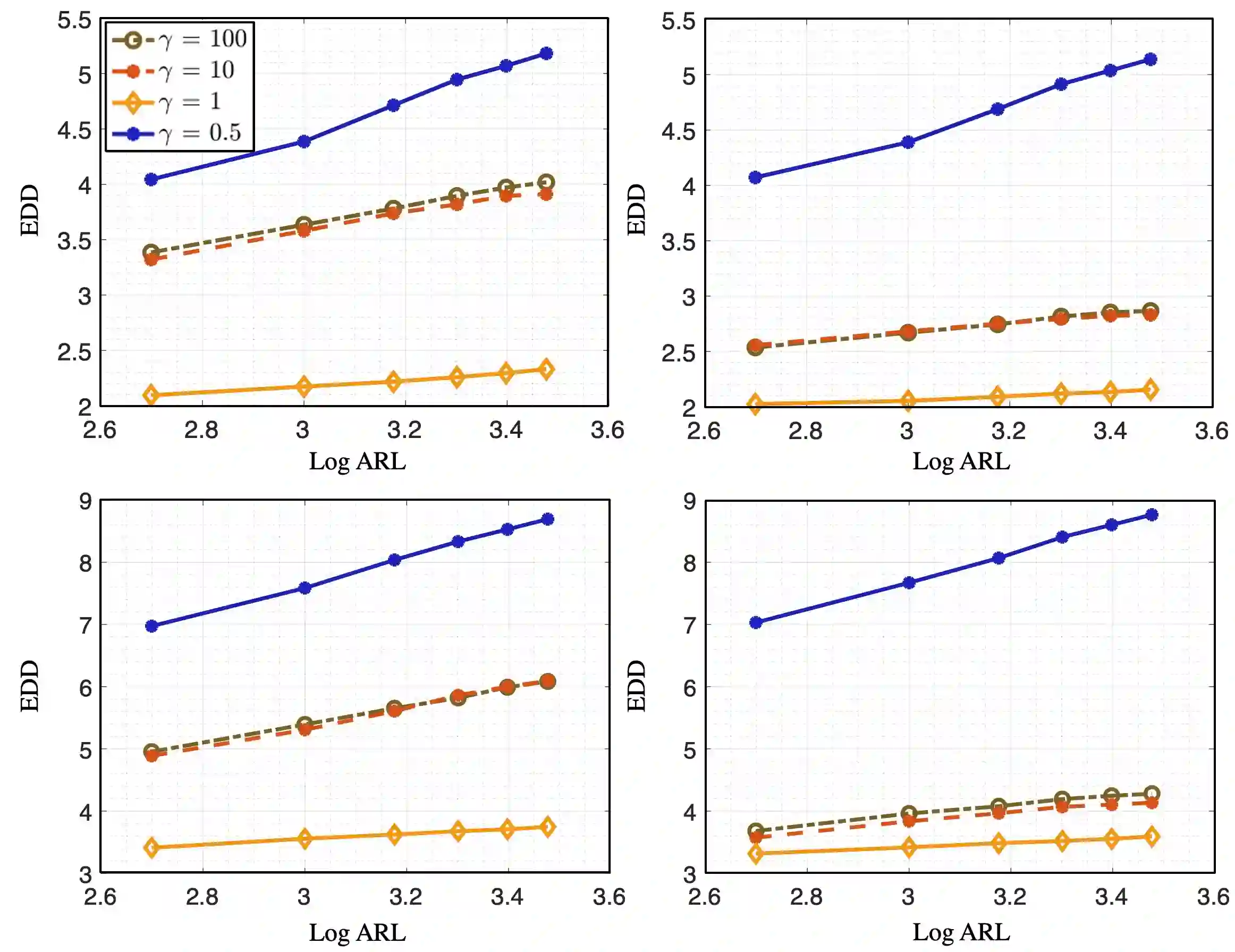
We present a computationally efficient online kernel Cumulative Sum (CUSUM) method for change-point detection that utilizes the maximum over a set of kernel statistics to account for the unknown change-point location. Our approach exhibits increased sensitivity to small changes compared to existing kernel-based change-point detection methods, including Scan-B statistic, corresponding to a non-parametric Shewhart chart-type procedure. We provide accurate analytic approximations for two key performance metrics: the Average Run Length (ARL) and Expected Detection Delay (EDD), which enable us to establish an optimal window length to be on the order of the logarithm of ARL to ensure minimal power loss relative to an oracle procedure with infinite memory. Moreover, we introduce a recursive calculation procedure for detection statistics to ensure constant computational and memory complexity, which is essential for online implementation. Through extensive experiments on both simulated and real data, we demonstrate the competitive performance of our method and validate our theoretical results.

翻译：本文提出了一种计算高效的在线核累积和（CUSUM）方法，用于变点检测。该方法通过在一组核统计量上取最大值来应对未知变点位置的问题。与现有的基于核的变点检测方法（包括对应于非参数Shewhart控制图类程序的Scan-B统计量）相比，我们的方法对小变化表现出更高的敏感性。我们为两个关键性能指标——平均运行长度（ARL）和预期检测延迟（EDD）——提供了精确的解析近似，这使我们能够确定最优窗口长度约为ARL的对数，以确保相对于具有无限记忆的预言机程序，功效损失最小。此外，我们引入了检测统计量的递归计算程序，以确保恒定的计算和内存复杂度，这对于在线实现至关重要。通过对模拟数据和真实数据的广泛实验，我们证明了该方法的竞争性能，并验证了我们的理论结果。