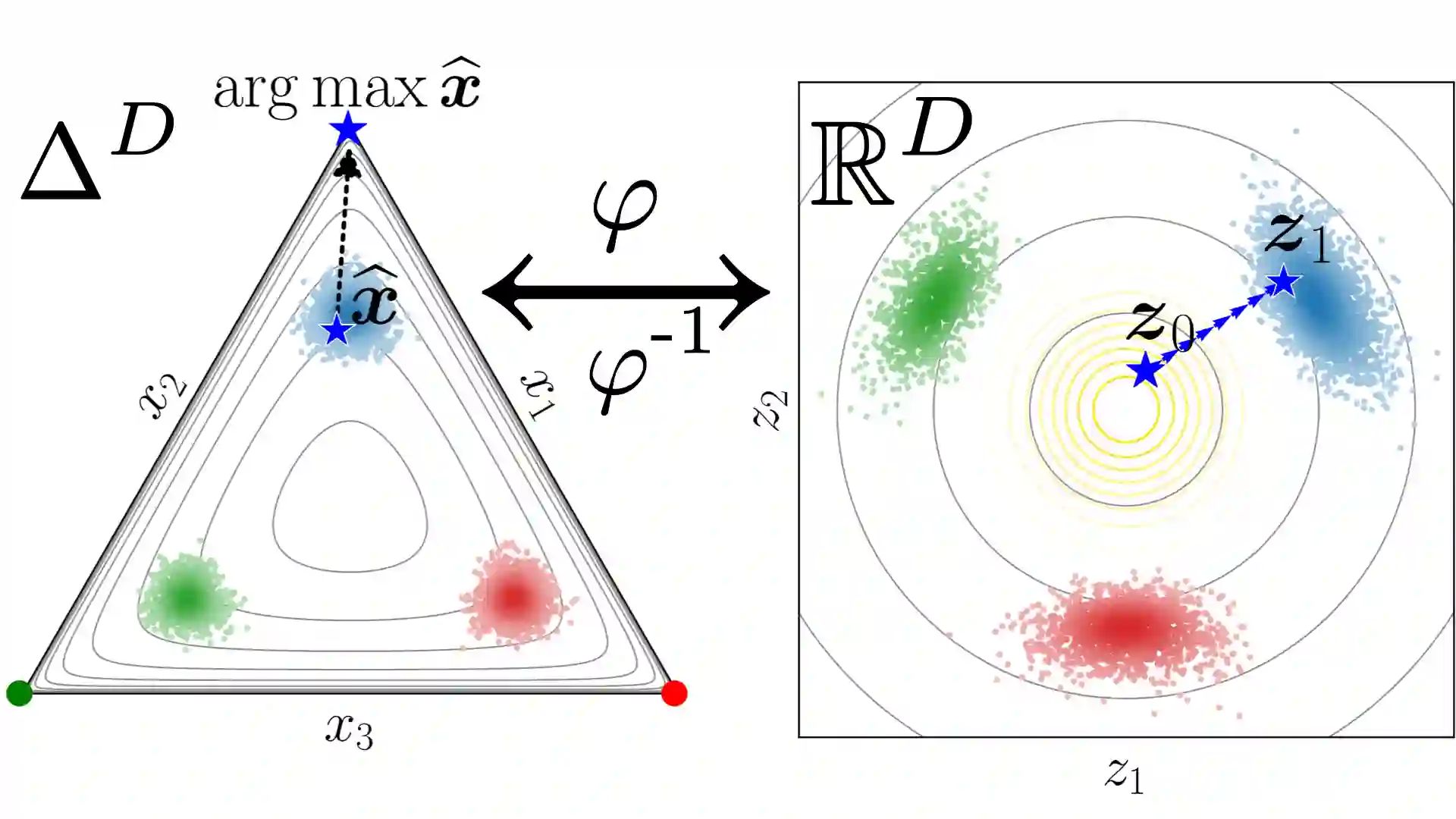
We propose a method for learning and sampling from probability distributions supported on the simplex. Our approach maps the open simplex to Euclidean space via smooth bijections, leveraging the Aitchison geometry to define the mappings, and supports modeling categorical data by a Dirichlet interpolation that dequantizes discrete observations into continuous ones. This enables density modeling in Euclidean space through the bijection while still allowing exact recovery of the original discrete distribution. Compared to previous methods that operate on the simplex using Riemannian geometry or custom noise processes, our approach works in Euclidean space while respecting the Aitchison geometry, and achieves competitive performance on both synthetic and real-world data sets.

翻译：我们提出了一种在单纯形支撑的概率分布上进行学习与采样的方法。该方法通过光滑双射将开单纯形映射至欧几里得空间，利用Aitchison几何定义映射关系，并通过狄利克雷插值将离散观测解量化为连续值以支持分类数据建模。这一设计使得我们能够借助双射在欧几里得空间中进行密度建模，同时仍能精确恢复原始离散分布。相较于以往基于黎曼几何或定制噪声过程在单纯形上操作的方法，我们的方法在遵循Aitchison几何的前提下于欧几里得空间中进行计算，并在合成与真实数据集上均取得了具有竞争力的性能。