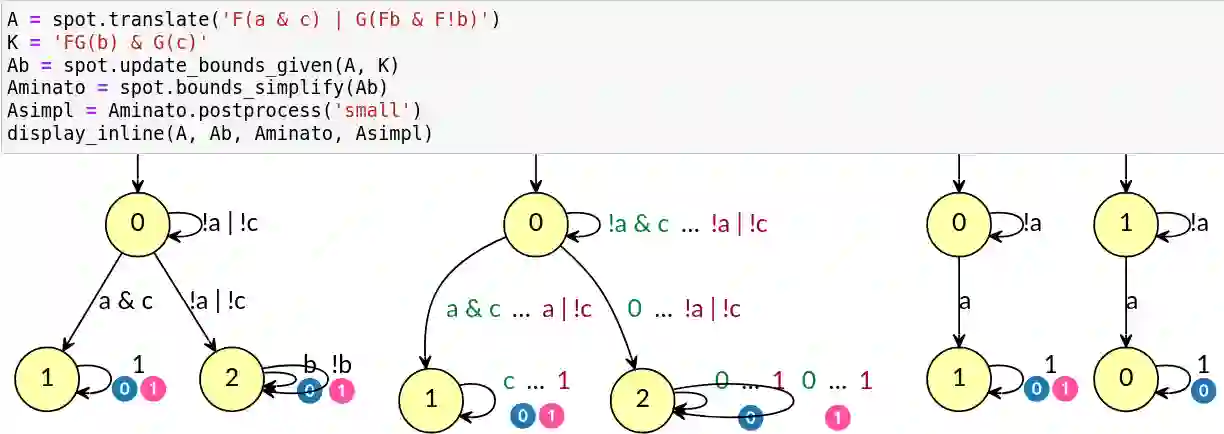
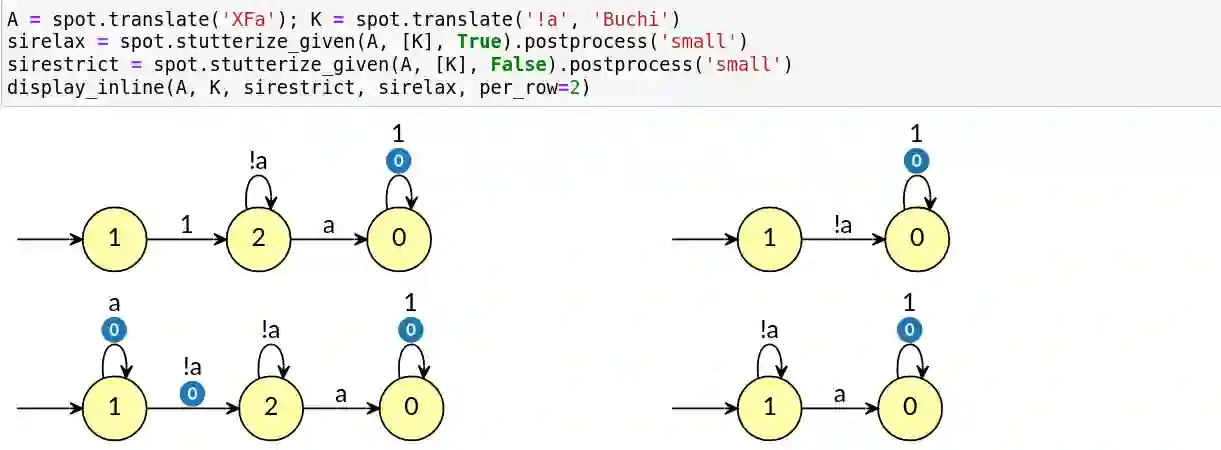
We consider the problem of the verification of an LTL specification $\varphi$ on a system $S$ given some prior knowledge $K$, an LTL formula that $S$ is known to satisfy. The automata-theoretic approach to LTL model checking is implemented as an emptiness check of the product $S\otimes A_{\lnot\varphi}$ where $A_{\lnot\varphi}$ is an automaton for the negation of the property. We propose new operations that simplify an automaton $A_{\lnot\varphi}$ \emph{given} some knowledge automaton $A_K$, to produce an automaton $B$ that can be used instead of $A_{\lnot\varphi}$ for more efficient model checking. Our evaluation of these operations on a large benchmark derived from the MCC'22 competition shows that even with simple knowledge, half of the problems can be definitely answered without running an LTL model checker, and the remaining problems can be simplified significantly.

翻译：我们考虑在给定系统$S$已知满足的LTL公式$K$作为先验知识的情况下，验证LTL规约$\varphi$的问题。LTL模型检验的自动机理论方法实现为对乘积$S\otimes A_{\lnot\varphi}$的 emptiness 检查，其中$A_{\lnot\varphi}$是属性否定的自动机。我们提出新的操作，在给定知识自动机$A_K$的情况下简化自动机$A_{\lnot\varphi}$，生成自动机$B$以替代$A_{\lnot\varphi}$从而实现更高效的模型检验。我们在源自MCC'22竞赛的大型基准测试中对这些操作进行评估，结果表明即使使用简单知识，半数问题无需运行LTL模型检验器即可确定解答，其余问题也可获得显著简化。