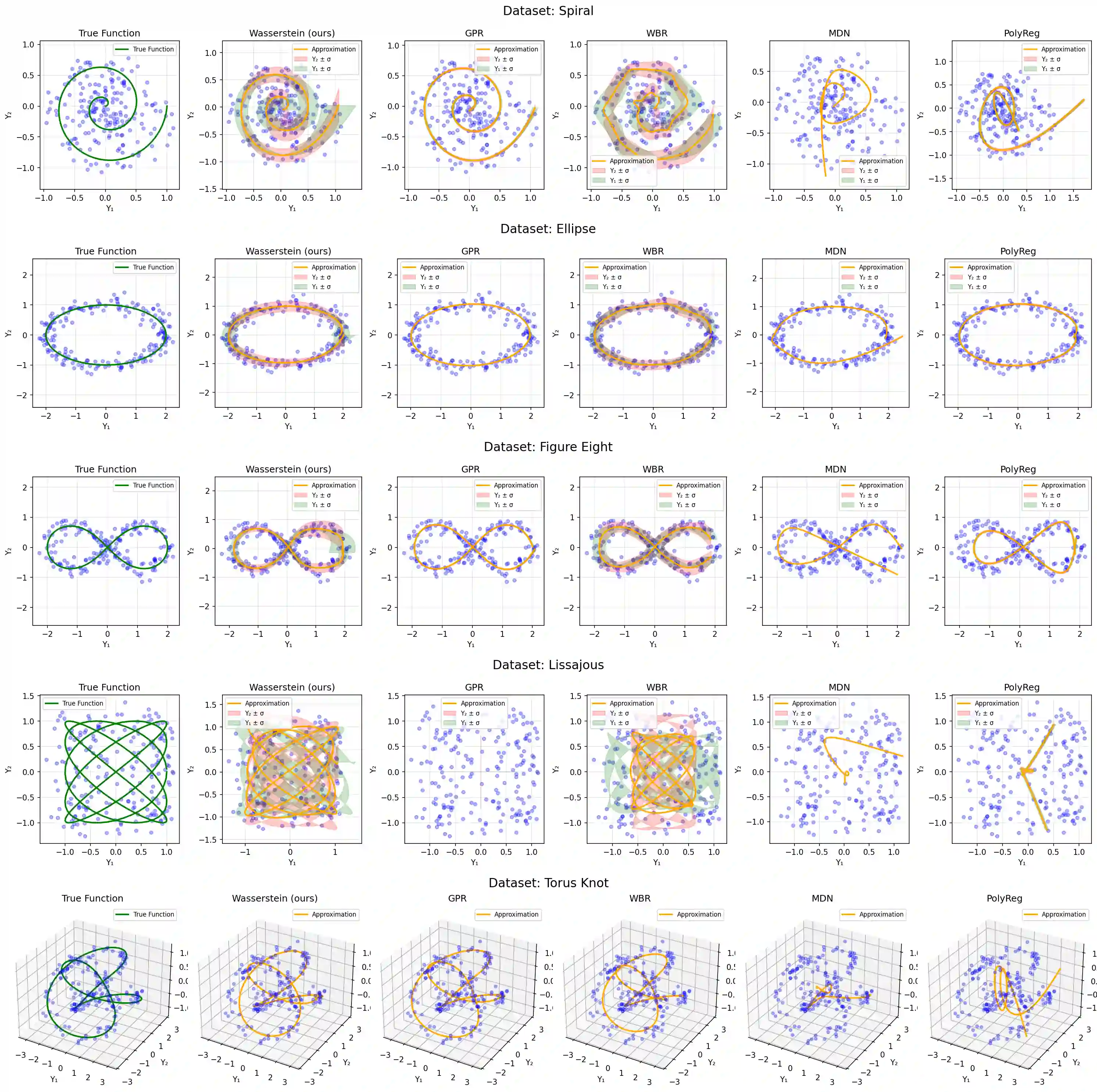
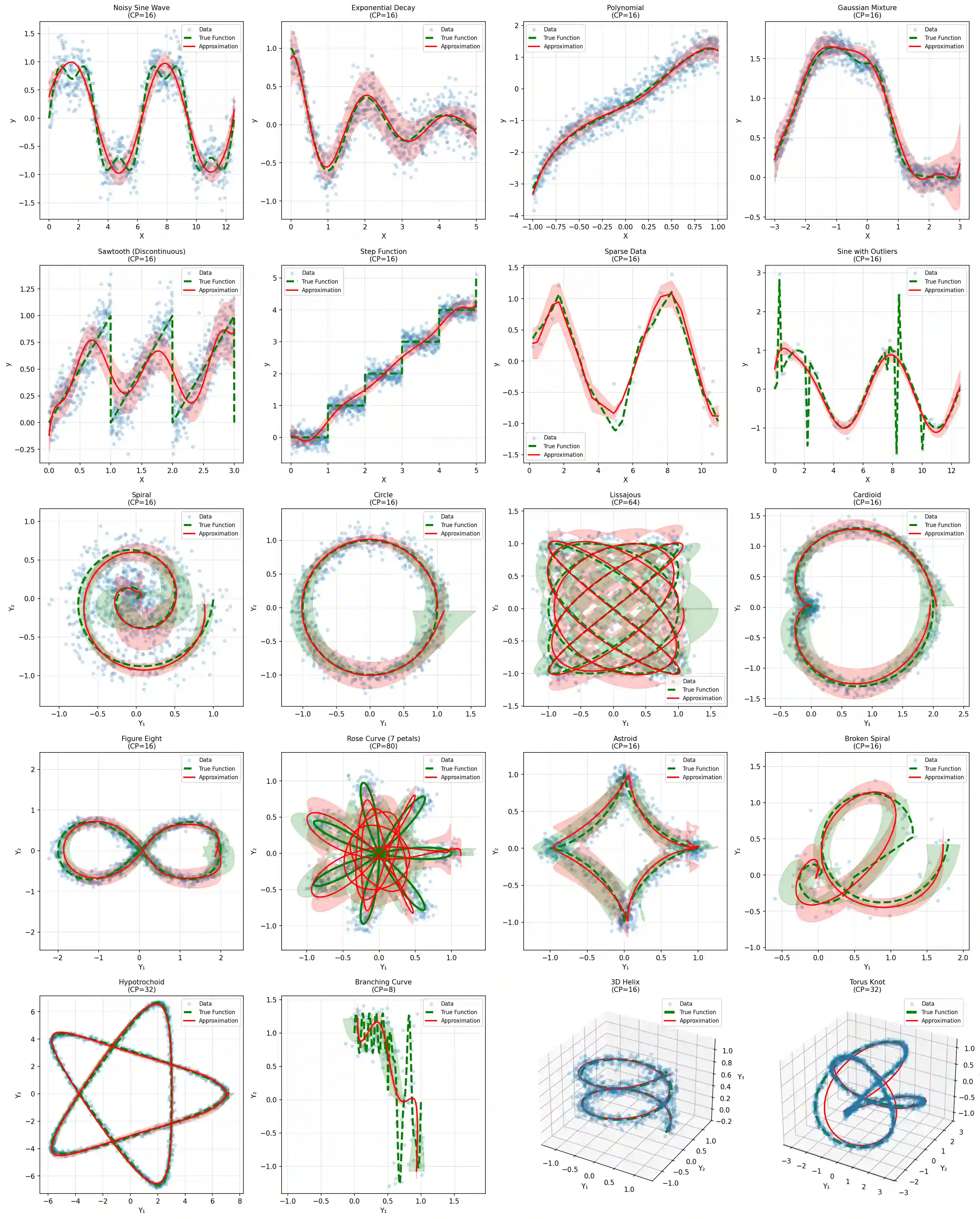
This paper considers the problem of regression over distributions, which is becoming increasingly important in machine learning. Existing approaches often ignore the geometry of the probability space or are computationally expensive. To overcome these limitations, a new method is proposed that combines the parameterization of probability trajectories using a Bernstein basis and the minimization of the Wasserstein distance between distributions. The key idea is to model a conditional distribution as a smooth probability trajectory defined by a weighted sum of Gaussian components whose parameters -- the mean and covariance -- are functions of the input variable constructed using Bernstein polynomials. The loss function is the averaged squared Wasserstein distance between the predicted Gaussian distributions and the empirical data, which takes into account the geometry of the distributions. An autodiff-based optimization method is used to train the model. Experiments on synthetic datasets that include complex trajectories demonstrated that the proposed method provides competitive approximation quality in terms of the Wasserstein distance, Energy Distance, and RMSE metrics, especially in cases of pronounced nonlinearity. The model demonstrates trajectory smoothness that is better than or comparable to alternatives and robustness to changes in data structure, while maintaining high interpretability due to explicit parameterization via control points. The developed approach represents a balanced solution that combines geometric accuracy, computational practicality, and interpretability. Prospects for further research include extending the method to non-Gaussian distributions, applying entropy regularization to speed up computations, and adapting the approach to working with high-dimensional data for approximating surfaces and more complex structures.

翻译：本文研究了分布回归问题，该问题在机器学习中日益重要。现有方法往往忽略概率空间的几何结构或计算成本高昂。为克服这些限制，提出了一种新方法，结合了使用Bernstein基的概率轨迹参数化和分布间Wasserstein距离的最小化。核心思想是将条件分布建模为一条平滑的概率轨迹，该轨迹由高斯分量的加权和定义，其参数——均值和协方差——是通过Bernstein多项式构建的输入变量的函数。损失函数是预测高斯分布与经验数据之间的平均平方Wasserstein距离，该距离考虑了分布的几何特性。采用基于自动微分的优化方法训练模型。在包含复杂轨迹的合成数据集上的实验表明，所提方法在Wasserstein距离、能量距离和均方根误差指标上提供了有竞争力的近似质量，尤其在非线性显著的情况下。该模型展示了优于或可与替代方法比拟的轨迹平滑性，以及对数据结构变化的鲁棒性，同时通过控制点的显式参数化保持了高可解释性。所开发的方法代表了一种结合几何精度、计算实用性和可解释性的平衡解决方案。进一步研究的前景包括将该方法扩展到非高斯分布、应用熵正则化以加速计算，以及将该方法适配于处理高维数据以近似曲面和更复杂的结构。