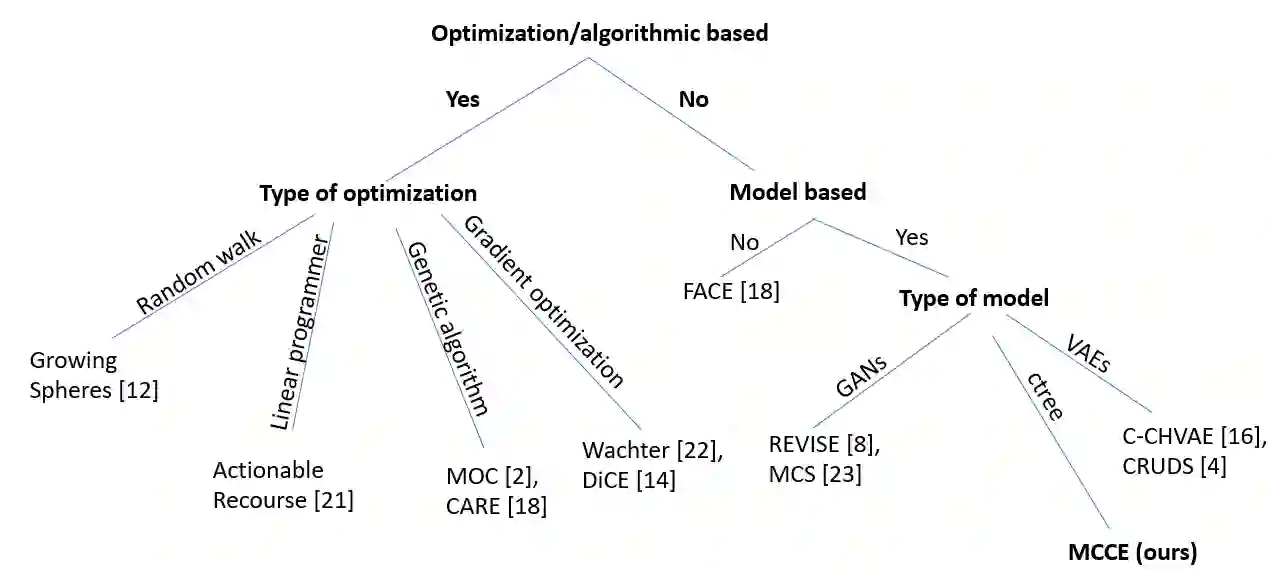
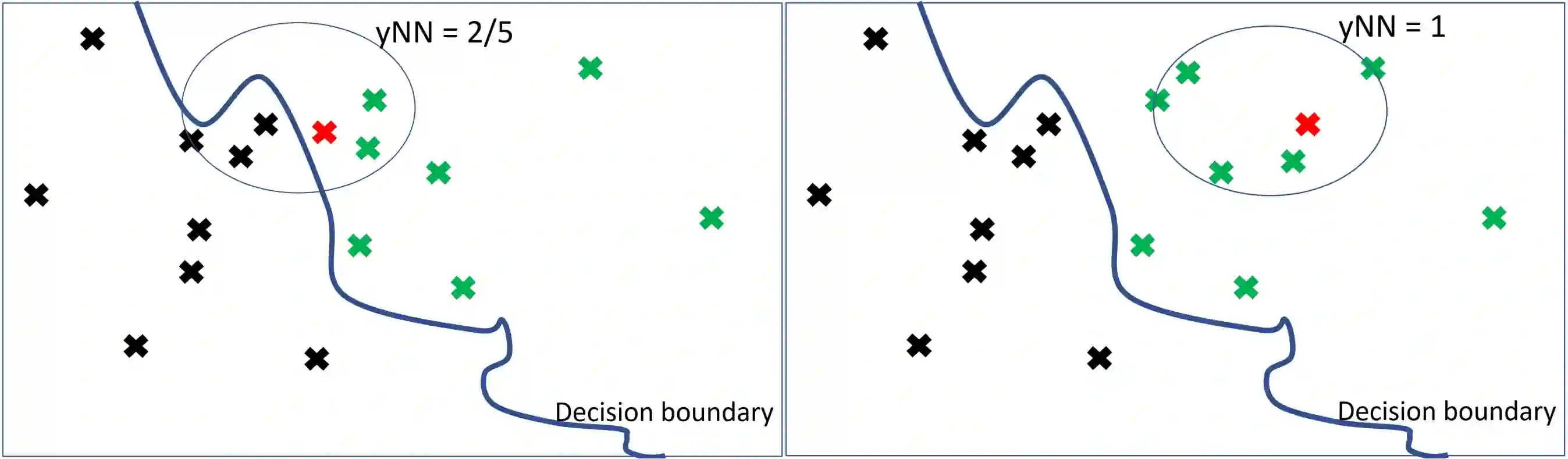
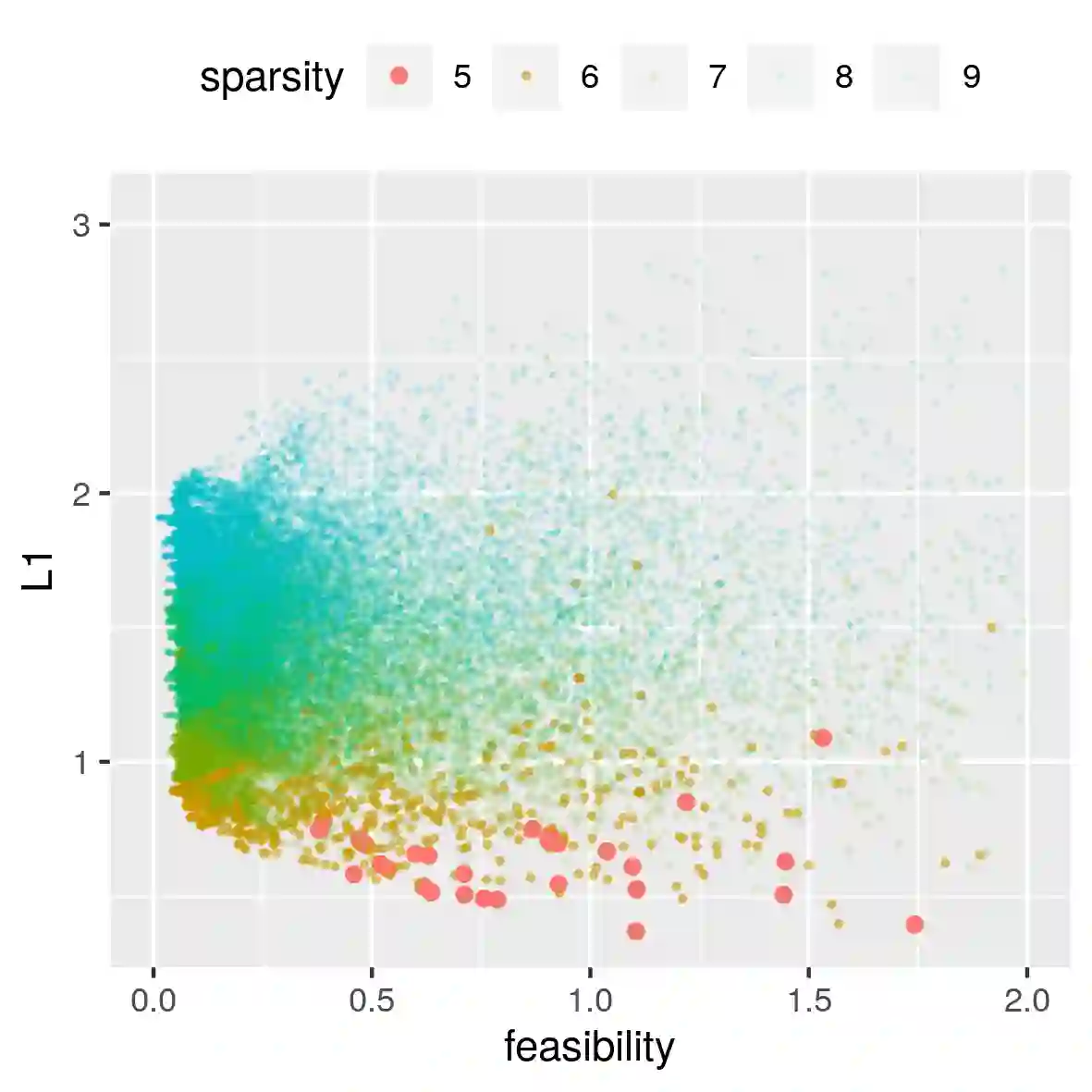
In this paper we introduce MCCE: Monte Carlo sampling of realistic Counterfactual Explanations, a model-based method that generates counterfactual explanations by producing a set of feasible examples using conditional inference trees. Unlike algorithmic-based counterfactual methods that have to solve complex optimization problems or other model based methods that model the data distribution using heavy machine learning models, MCCE is made up of only two light-weight steps (generation and post-processing). MCCE is also straightforward for the end user to understand and implement, handles any type of predictive model and type of feature, takes into account actionability constraints when generating the counterfactual explanations, and generates as many counterfactual explanations as needed. In this paper we introduce MCCE and give a comprehensive list of performance metrics that can be used to compare counterfactual explanations. We also compare MCCE with a range of state-of-the-art methods and a new baseline method on benchmark data sets. MCCE outperforms all model-based methods and most algorithmic-based methods when also taking into account validity (i.e., a correctly changed prediction) and actionability constraints. Finally, we show that MCCE has the strength of performing almost as well when given just a small subset of the training data.

翻译：在本文中,我们引入了中链氯化石蜡:蒙特卡洛对现实的反事实解释的抽样,这是一种基于模型的方法,通过利用有条件的推断树制作一系列可行的实例,产生反事实解释。与基于逻辑的反事实方法不同,这些方法必须解决复杂的优化问题,或采用重型机器学习模型来模拟数据分配的其他基于模型的方法,中链石灰岩中链只由两个轻量级步骤(生成和后处理)组成。中链石灰岩中链对于终端用户来说也是直截了当的,可以理解和实施,处理任何类型的预测模型和特征类型,在生成反事实解释时考虑到可操作性限制,并产生所需的许多反事实解释。在本文件中,我们介绍中链中链并列出一个全面的业绩计量清单,用以比较反事实解释。我们还将中链元件中链与一系列最新工艺方法和基准数据集的新基线方法进行比较。中链将所有基于模型的方法和大多数基于算法的方法都与考虑到有效性(即正确改变的预测)和可操作性限制结合起来。最后,我们在进行中显示中微的数据集。